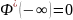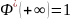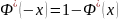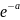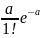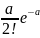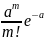Нормальное распределение.
График дифференциальной функции нормального распределения называют нормальной кривой (кривой Гаусса).
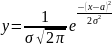
а – соответствует мат. ожиданию
σ – среднее квадратическое отклонение
Исследуем функцию методами дифференциального исчисления.
D=R – функция определена на всей оси х.
нормальная кривая расположена над осью х.
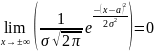– ось
х служит горизонтальной асимптотой
графика.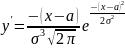
.
y'=0
при x=a,
y’>0
при x<a,
y’<0
при x>a.
При x=a
функция имеет максимум, равный
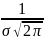.Разность х-а содержится в аналитическом выражении функции в квадрате, то есть график функции симметричен относительно прямой х=а.
.
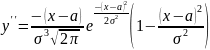При х=а+σ и х=а-σ
,
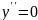а при переходе через эти точки она
меняет знак.
Точки
перегиба:
.
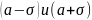Нормальная кривая сдвигается вправо, если параметр а возрастает и влево, если а убывает. Чем больше σ, тем кривая более сжимается к оси х, и наоборот.
Вероятность попадания в заданный интервал нормальной случайной величины.
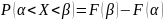
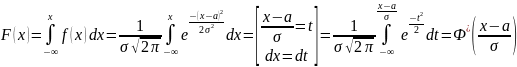
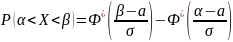
Свойства Функции Лапласа:
Вероятность попадания случайной величины, распределённой по нормальному закону:
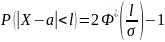
Правило «трёх сигма».
Преобразуем формулу
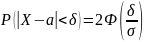
положив
.
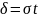В итоге получим:
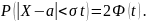
Если
t=3
и, следовательно,
,
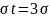то
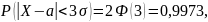
То есть вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратической отклонение, очень мала. Такое событие можно считать невозможным.
Правило трёх сигм: Если случайная величина распределена нормально, то абсолютная величина её отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.
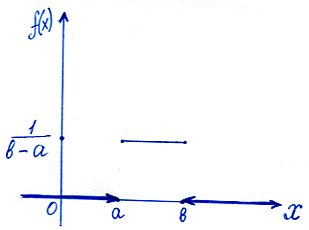
Равномерное распределение.
Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, дифференциальная функция имеет постоянное значение.
Найдём
дифференциальную функцию равномерного
распределения, считая, что все возможные
значения случайной величины заключены
в интервале (a,
b),
на котором дифференциальная функция
сохраняет постоянное значение
.
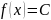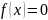при
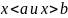
Найдём значение С.
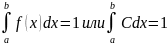
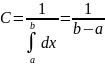
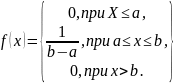
Закон Пуассона.
Рассмотрим дискретную случайную величину Х, которая может принимать только целые, не отрицательные значения. Говорят, что случайная величина Х распределена по закону Пуассона, если вероятность того, что она примет определенное значение m, выражается формулой:
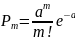
Где а – некоторая положительная величина, называемая параметром Пуассона.
Ряд распределения случайной величины X, распределённой по закону Пуассона, имеет вид:
Хm |
0 |
1 |
2 |
… |
m |
… |
Pm |
|
|
|
… |
|
… |
Убедимся,
что сумма всех вероятностей
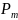равна 1.
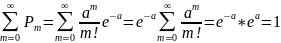
По определению математического ожидания:
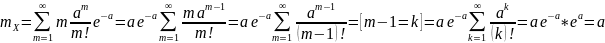
Для определения дисперсии найдём второй начальный момент Х:
Находим дисперсию:
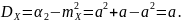
Равенство мат. ожидания и дисперсии применяется на практике для решения вопроса, правдоподобия гипотезы о том, что случайная величина Х распределена по закону Пуассона.