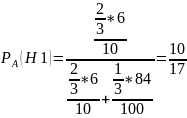Теорема умножения вероятностей.

Вероятность совместного появления двух независимых событий А и В равна произведению вероятностей этих событий.

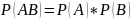
Доказательство: Пусть n – число возможных исходов, в которых событие А наступает или не наступает. n1 – число исходов, благоприятных событию А. m – число возможных исходов, в которых событие В наступает или не наступает. m1 – число исходов благоприятных событию В. mn – число всех возможных событий. m1n1 – число совместных появлений событий А и В.

Вероятность совместного появления событий А и В:

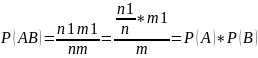
Следствие: вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий.

Условная вероятность.

Вероятность произведения двух событий A и В равна произведению вероятности одного события на вероятность другого, вычисленная при условии, что первое произошло.

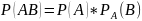
Доказательство:

Пусть n – число всех случаев, m – число случаев, благоприятных А, k – число случаев, благоприятных В, l – число случаев, благоприятных и А, и В.

………………………………………………

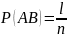
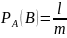
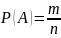
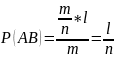
7. Формула полной вероятности.

Пусть требуется определить вероятность некоторого события А, которое может произойти вместе с 1 из событий Н₁, Н₂,…,Н_n, образующих полную группу несовместных событий, называемых гипотезами.

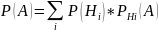
Доказательство:

Так как гипотезы образуют полную группу, то событие А может появиться в комбинации из этих гипотез.

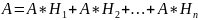
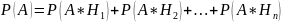
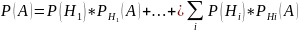
Пример: В урну, содержащую 2 шара, опущен белый шар, после чего из неё наудачу вынут 1 шар. Найти вероятность того, что вынули белый шар.

Решение:

Так как нам не известно, какого цвета были шары в урне, выдвинем следующие гипотезы:

H1 – изначально был только 1 белый шар в ящике

Н2 – изначально в ящике лежало 2 белых шара

Н3 – изначально в ящике не было шаров белого цвета

Вероятность появления каждой из этих гипотез равна 1/3 (по формуле классической вероятности).

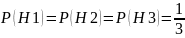
Вычислим вероятность вытащить белый шар из трёх уже имеющихся в ящике при условии каждой отдельной гипотезы.

1. В ящике находится 2 белых шара из 3. Значит, по формуле классической вероятности:

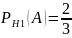
2. В ящике находится 3 белых шара из 3. Это достоверное событие, его вероятность равна 1.

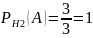
3. В ящике находится 1 белый шар из 3.

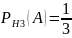
По формуле полной вероятности получаем:

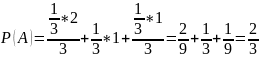
8. Формула Бейеса.

Имеется полная группа несовместных гипотез H_i. Вероятность их до опыта известна. В результате опыта произошло событие А. Как следует изменить вероятность гипотез в связи с тем, что произошло событие А?

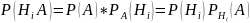
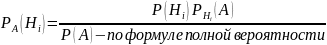
Пример: 2 станка производят детали, поступающие на общий конвейер. Производительность 1-ого станка в 2 раза больше 2-ого. Первый станок производит 60% деталей, второй – 84% деталей отличного качества. Взятая с конвейера деталь оказалась отличного качества. Определить вероятность того, что деталь с первого станка.

Решение:

Событие А – взяли деталь отличного качества.

Выдвигаем гипотезы:

Н1 – взяли деталь с первого станка

Н2 – взяли деталь со второго станка

-?

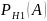Производительность первого станка = 2х, а второго = х. Значит, их общая производительность равна 3х. Согласно этим данным, можно определить вероятности того, что взятая деталь была произведена первым или вторым станком.

P(H1)=2/3;

P(H2)=1/3.

Теперь найдём вероятность того, что взятая с первого конвейера деталь оказалась отличного качества. .

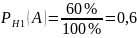Аналогично, вероятность того, что взятая со второго конвейера деталь оказалась отличного качества: .

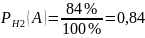По формуле Бейеса получаем: