3. Тензор напружень. Найбільші дотичні напруження.

Через кожну точку тіла можна провести скільки завгодно площадок, які нахилені по відношенню до всіх трьох координатних площин. Аналіз формули (2.1) дозволяє дійти висновку, що для визначення напружень на будь-якій похилій площадці достатньо знати напруження на трьох взаємно перпендикулярних площадках. Таким чином, дев’ять складових напружень σ_x, τ_xy, τ_xz, τ_yx, σ_y, τ_yz, τ_zx, τ_zy, σ_z (з них шість дорівнюють попарно) повністю визначають напружений стан в точці.

На кожній координатній площадці три складові утворюють вектор повного напруження: на площадці з нормаллю х – вектор Р_х, на площадці з нормаллю y – P_y, на площадці з нормаллю z – P_z. Сукупність трьох векторів Р_х, P_y, P_z визначаються дев’ятьма складовими, які при зміні координатних осей перетворюються за формулою (2.1), називаються афінним ортогональним тензором другого рангу. Тензором першого рангу є вектор. На далі будемо називати його тензором, а дев’ять складових – компонентами тензора.

Тензор, компонентами якого є напруження та описує напружений стан в точці називають тензором напружень. Останній записують в наступному вигляді:

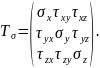(2.10)

В строках тензора записані напруження, напрямок яких паралельний, відповідно, координатним осям x, y, z, а в стовпцях – напруження на площадці, нормаль до якої паралельна вісі x, або y, або z.

Спираючись на закон парності дотичних напружень, можна стверджувати, що компоненти тензора напружень, які розташовані симетрично відносно головної діагоналі, дорівнюють одне одному, тому тензор напружень Т_σ є симетричним.

В кожній точці пружного тіла буде свій тензор напружень, відповідно, в тілі існує поле тензорів напружень.

Властивості тензора:

1. Тензори можна складати та віднімати. Сумою двох тензорів буде новий тензор, компоненти якого представляють собою суму відповідних компонентів тензора, що складаються;

2. Тензор можна множити на скаляр. Добуток тензора на скаляр λ дасть новий тензор, компоненти якого в λ разів більше відповідних компонентів тензора, що перемножують.

Розглянемо напружений стан, при якому на трьох взаємно перпендикулярних площадках діють тільки три однакових головних напруження σ₀, які дорівнюють середньому напруженню в розглядуваній точці тіла:

. (2.11)

Такий напружений стан описують тензором, який носить назву кульового тензора напружень:

(2.12)

Назва “кульовий тензор” пов’язана з запропонованим Моне геометричним уявленням про напружений стан в точці. Якщо в системі координат, що співпадає з головними осями, для кожної площадки, яка проходить через початок координат, побудувати вектор повного напруження Р_ν, то кінці цих векторів опишуть поверхню еліпсоїда, що носить назву еліпсоїда напружень або еліпсоїда Ламе.

Три півосі еліпсоїда напружень дорівнюють за довжиною дорівнюють трьом головним напруженням. У випадку напруженого стану, який можна описати кульовим тензором, всі три напруження дорівнюють одне одному і еліпсоїд напружень перетворюється на шар.

Використовуючи другу згадувану властивість тензора, кульовий тензор можна представити у вигляді:

де

представляє собою так званий одиничний тензор.

Якщо відняти від тензора напружень (2.10) кульовий тензор (2.12), отримаємо тензор, який називають девіатором напружень, а саме:

(2.13)

Таким чином, тензор напружень в кожній точці може бути представлений у вигляді суми двох тензорів: кульового тензора напружень та девіатора напружень (рис. 2.3), тобто:

. (2.14)

Р озкладання тензора напружень на кульовий та девіатор має велике принципове значення при дослідженні поведінки пружних та пластичних тіл під навантаженням. Кульовий тензор σ₀Т₁ виділяє з напруженого стану рівномірне всебічне розтягання (стискання), при якому змінюються лише об’єм розглядуваного елемента тіла без зміни форми. Девіатор напружень D_σ характеризує стан зсуву, при якому змінюється форма елемента без зміни його об’єму. Відповідно, девіатор напружень вказує відхилення (девіацію) розглядуваного напруженого стану від всебічного розтягання (стискання) або відхилення, якого набуло тіло у порівнянні з початковою його формою.

Інваріанти напруженого стану (2.8) або (2.9) можна розглядати як такі, що складаються з компонентів тензора напружень, тому їх називають також інваріантами тензора напружень.

Перший інваріант девіатор напружень:

.

Після підстановки в цей вираз формули (2.11) для розрахунку середнього напруження та перетворень отримаємо:

.

Зробимо такі ж дії по відношенню до другого інваріанта:

Після відповідних перетворень отримаємо:

(2.15)

Другий інваріант девіатор напружень відіграє суттєву роль в теорії пластичності, де зазвичай розглядають величину, пропорційну квадратному кореню з цього інваріанту та носить назву – інтенсивність дотичних напружень, а саме:

(2.16)

Остання представляє собою дотичне напруження на площадках однаково нахилених до всіх трьох головних напружень.

Замість інтенсивності дотичних напружень часто розглядають пропорційну до неї величину, яку називають – інтенсивність напружень, а саме:

(2.17)

Числовий коефіцієнт в останній формулі обрано таким чином, щоб при простому розтяганні інтенсивність напружень дорівнювала нормальному напруженню. Дійсно при осьовому розтяганні σ_x = σ, σ_y = σ_z = τ_xy = τ_yz = τ_zx = 0.

Якщо підставити ці величини в формулу (2.17) отримаємо:

В теорії пластичності потрібно знати величину найбільших дотичних напружень. З курсу “Опір матеріалів” відомо, що для кожної сукупності площадок, які паралельні трьом головним напруженням, можна знайти екстремальні значення дотичних напружень:

(2.18)

Одне з цих значень максимальне:

(2.19)

Для подальшого вивчення дисципліни ведемо поняття направляючого тензора напружень, яким називають девіатор напружень, кожний компонент якого поділено на інтенсивність напружень:

(2.20)

Направляючий тензор напружень визначає тільки головні напрямки напружень та співвідношення між компонентами тензора напружень, але не визначає його значення, оскільки компоненти направляючого тензора напружень – величини безрозмірні.