Дифференциальное уравнение гармонических колебаний или уравнение гармонического осциллятора

Составим уравнения Лагранжа для двух конкретных механических систем.

Гармонический осциллятор — это грузик на гладком стержне, поддерживаемый с двух концов пружинами. Для него в качестве единственной обобщенной координаты можно взять декартову координату x; для маятника естественно выбрать φ (см. рис. 1). Тогда уравнения (2) для этих систем запишутся в виде

r =  ( x 0 0 ) ;

r =  ( t·sin φ 0 – t·cos φ ) ;

Для маятника эта функция взаимно однозначна при φ ∈ (–π, π) и при φ ∈ (0, 2π) (две локальные системы координат). Далее, кинетическая энергия этих механических систем вычисляется по формулам

T = mx.2 2

T = m 2 [(tφ.cos λ)2 + (tφ.sin λ)2] = 1 2 mt2φ.2,

а обобщенные силы — по формулам

Q = – kx · ( 1 0 0 ) · ∂r ∂x = –kx · ∂r ∂x

Q = –mg · ( 0 0 1 ) · ∂r ∂φ = –mg · ∂r ∂φ = –mgt ·sin φ

(в гармоническом осцилляторе это сила пружин по закону Гука, а в маятнике — сила земного тяготения). Промежуточные вычисления тривиальны:

∂T ∂q1  =  ∂T ∂x.  = mx.;

∂T ∂q.1  =  ∂T ∂φ  = ml2φ.;

d dt ∂T ∂q1  = mx..;

d dt ∂T ∂q1  = ml2φ..;

∂T ∂q1  =  ∂T ∂x  = 0;

∂T ∂q1  =  ∂T ∂φ  = 0.

Таким образом, уравнения движения имеют вид:

mx.. = –kx;

ml2φ.. = –mgl·sin φ,

или в окончательном виде, для гармонического осциллятора:

x.. + ω2x = 0    (ω2 = k/m),

(3)

а для маятника:

φ.. + ω2sin φ = 0    (ω2 = g/l).

(4)

Определение амплитуды и начальной фазы колебаний по начальным условиям

Для определения амплитуды и начальной фазы необходимо задать начальные условия. Пусть, например, в начальный момент t = 0 положение груза x=x₀ и скорость u=u₀. Тогда   , откуда 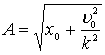,  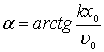       Из формул для амплитуды и начальной фазы видно, что в отличие от частоты и периода собственных колебаний они зависят от начального состояния системы. При отсутствии начальной скорости (u₀=0) амплитуда А=х₀, а начальная фаза a=p/2 и, таким образом, 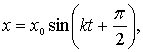  или    

Энергия гармонических колебаний

При механических колебаниях колеблющееся тело (или материальная точка) обладает кинетической и потенциальной энергией. Кинетическая энергия тела W: (Скорость тела v = ds/dt) Для вычисления потенциальной энергии тела воспользуемся самой общей формулой, связывающей силу и потенциальную энергию тела в поле этой силы: где U - потенциальная энергия, набираемая (или теряемая) телом, движущимся в силовом поле F от точки 0 (точки, в которой потенциальная энергия принимается равной 0) до точки х.     Для силы, линейно зависящей от смещения (как в случае наших механических маятников, такие силы носят общее название квазиупругих сил) мы имеем: Сравнивая формулы для кинетической и потенциальной энергии механического маятника, можно сделать следующие выводы: 1. Полная механическая энергия тела не изменяется при колебаниях: 2. Частота колебаний кинетической и потенциальной энергии в 2 раза больше частоты колебаний маятника. 3. Колебания кинетической и потенциальной энергии сдвинуты друг относительно друга по фазе на  (на полпериода). Когда кинетическая энергия достигает максимума, потенциальная - минимума (нуля) и наоборот. Энергия при колебаниях постоянно перекачивается из потенциальной в кинетическую и обратно. В случае электрических колебаний энергия в конуре представляет собой сумму энергии электрического поля, запасенной между обкладками конденсатора, и энергии магнитного поля, запасенной в катушке с индуктивностью. Вычислим обе составляющие. Сравнивая эти формулы, можно сделать следующие выводы: 1. Полная энергия в контуре остается неизменной: 2. Частота колебаний энергий в 2 раза превосходит частоту колебаний заряда и тока в контуре. 3. Электрическая и магнитная энергии сдвинуты по фазе на полпериода друг относительно друга; происходит непрерывное перекачивание энергии из одной формы в другую и обратно. Поскольку в контуре происходят колебания электрической и магнитной энергий, электрический колебательный контур также называют электромагнитным.