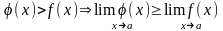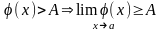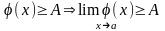- •1. Числовые последовательности. Ограниченные и неограниченные множества. Верхние и нижние грани множества.
- •2. Бесконечно малые и бесконечно большие последовательности. Свойства бесконечно малых последовательностей. Теорема связи между бесконечно большими и бесконечно малыми последовательностями.
- •3. Предел числовой последовательности Теорема о единственности предела. Критерии Коши.
- •4. Сходящиеся числовые последовательности. Теорема об ограниченности сходящейся числовой последовательности. Свойства сходящихся числовых последовательностей.
- •5. Теорема о предельном переходе в неравенствах. Теоремы о промежуточной последовательности.
- •6. Монотонные последовательности. Теорема о сходимости монотонной ограниченной последовательности.
- •7. Теорема о вложенных отрезках.
- •8. Число Эйлера (“e”).
- •9. Понятие функции, способы ее задания. Классификация функций.
- •10. Два определения предела функции в точке. Теорема об эквивалентности определений пределов функции в точке.
- •11.Теорема о пределе суммы, произведения, и частной функции. Предел функции на бесконечности. Теорема об ограниченности функции, имеющей предел.
- •12. Односторонние пределы. Теоремы о переходе к пределу в неравенствах.
- •13. Теорема о 1-м замечательном пределе.
- •14.Теоремы о 2-м замечательном пределе.
- •15. Бесконечно малые и бесконечно большие функции, сравнение бесконечно малых функций, эквивалентные бесконечно малые. Связь между бесконечно большими и бесконечно малыми
- •16. Непрерывность функции в точке. Примеры. Свойства непрерывных в точке функций. Теорема о непрерывности сложной функции.
- •17. Теорема о непрерывности обратной функции. Критерий непрерывности функции в точке. Односторонняя непрерывность.
- •18.Бесконечные пределы ф-ии.
- •19. Понятие непрерывности ф-ии.
- •20. Общие свойства ф-ии, непрерывной в точке.
- •Непрерывность и арифметические операции
- •Непрерывность сложной ф-ии.
- •21. Непрерывность ф-ии на множестве.
- •22. Характеристика точек разрыва ф-ии.
- •23. Односторонняя непрерывность ф-ии.
- •Свойства ф-й, непрерывных на отрезке
- •24. Дифференциальное счисление.
- •25. Определение призводной ф-ии в точке.
- •26. Степень ф-ии с вещественным показателем.
- •27. Геометрический смысл производной.
- •28. Дифференцируемость ф-ии.
- •29. Производная суммы, произведения, частного.
- •31. Производная от обратной ф-ии.
- •32. Производная от обратной ф-ии.
- •Производная от сложной ф-ии.
- •Односторонние производные.
- •33. Производная от параметрически заданной ф-ии.
- •34. Производные высших порядков.
- •35. Теоремы о дифф. Ф-ях.
- •36. Приложение производной к исследованию ф-ий.
- •37. Исследование ф-ии на выпуклость графика.
- •38. Асимптоты графика ф-ии.
- •Общая схема исследования ф-ий
- •39. Приложение производной к вычислению пределов.
- •40. Дифференциал ф-ии.
17. Теорема о непрерывности обратной функции. Критерий непрерывности функции в точке. Односторонняя непрерывность.
Теорема (о непрерывности обратной функции).
Пусть
функция
,
определена, строго монотонна и непрерывна
на некотором промежутке
![]() и пусть
и пусть
![]() - множество ее значений. Тогда на множестве
обратная функция однозначна, строго
монотонна и непрерывна.
- множество ее значений. Тогда на множестве
обратная функция однозначна, строго
монотонна и непрерывна.
Переход к пределу в неравенстве
Теорема: Пусть f(х) и j(х) имеют конечные пределы в т. y=a, тогда справедливо:
Доказательство:
Пусть
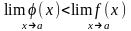 ,
тогда по общему свойству №6
,
тогда по общему свойству №6
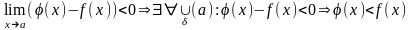 ,
,
а это противоречит 1
Замечание:
Из утверждения №3 следует, что предел неотрицательной ф-ии является неотрицательным.
При пределов к противоположным можно обе части умножать на (-1).
Теорема
2(о двух миллиционерах ) Пусть в некоторой
области Д выполняется система неравенств
 и а
– предел точки.
и а
– предел точки.
Пусть
существуют равные пределы
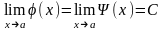 ,
,
тогда
существует
 .
.
Доказательство:
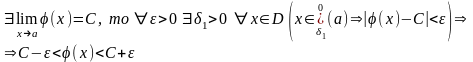
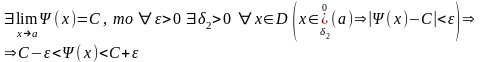
18.Бесконечные пределы ф-ии.
Если в общем определении предела через окрестности положить в качестве А бесконечно удаленную точку, то получим определение бесконечного предела.
Так как различают три вида бесконечно удаленных точек, то существуют три определения:
1.

2.
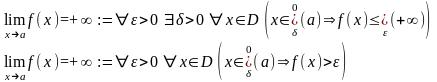
3.
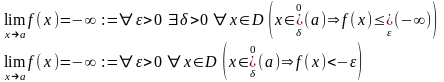
19. Понятие непрерывности ф-ии.
Непрерывность – такое свойство ф-ии, как отсутствие точек разрыва у графиков этой ф-ии. Т.е. строится единственной непрерывной линией.
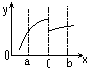
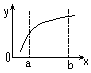
График непрерывной ф-ии ; График ф-ии, разрывной в т. С;
1.Ф-ия
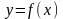 называется непрерывной в точке х0
, если предел
в
данной точке совпадает со значением
ф-ии в этой же точке
называется непрерывной в точке х0
, если предел
в
данной точке совпадает со значением
ф-ии в этой же точке

2.
3.
Разность
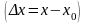 -приращение
аргумента в точке х0
-приращение
аргумента в точке х0
4.
Разность
 -
приращение ф-ии в точке х0
вызывает приращение аргумента
-
приращение ф-ии в точке х0
вызывает приращение аргумента
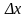
5. Ф-ия называется непрерывной в точке х0 , если бесконечно малому аргументу соответствует бесконечно малое значение ф-ии в точке х0 .
20. Общие свойства ф-ии, непрерывной в точке.
Представим ф-ию с помощью бесконечно малых
1.
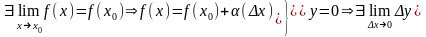
2.Пусть ф-ия непрерывна в точке х0 и ее значение в этой точке отлично от нуля, то существует целая окрестность х0 , в которой ф-ия не равна нулю и сохраняет знак f(x0)
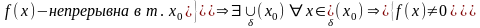
sign(х)(сигнум)
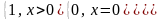
Доказательство:
а)
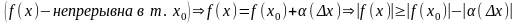
б)
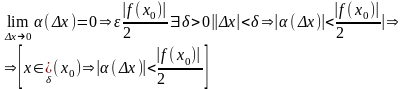
Из а) и б) следует:

Непрерывность и арифметические операции
Пусть
и
 непрерывна
в т. х0
, тогда справедливо:
непрерывна
в т. х0
, тогда справедливо:
Сумма этих ф-ий непрерывна в т. х0 ;
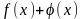 -
непрерывна в точке х0
-
непрерывна в точке х0
2. Произведение этих ф-ий непрерывно в т. х0
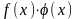 -
непрерывна в точке х0
-
непрерывна в точке х0
3. Отношение этих функций непрерывно в тех точках, в которых знаменатель отличен от нуля, т.е. если знаменатель ¹0.
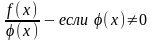
Доказательство:
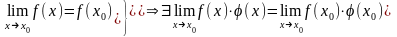
Непрерывность сложной ф-ии.
Пусть:
|
Þтогда
сложная ф-ия
|
Доказательство:
А).

Б).
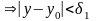
из А) и Б) следует:
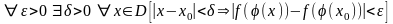
Sl.
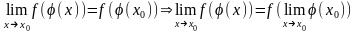
21. Непрерывность ф-ии на множестве.
Df. Ф-ия непрерывна на множестве Х , если она непрервна в каждой точке этого меожества.
Непрерывность обратной ф-ии:
Пусть - непрерывна и строго монотонна на промежуте Х , тогда справедливо:
*****
На промежутке Y существует непрерыная обратная ф-ия
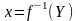 .
.Характер монотонности обратной ф-ии такой же как и прямой.
Непрерывность элементарной ф-ии:
**********
Доказательство непрерывности основной элементарной ф-ии tg и ctg , следует из свойств непрерыности элементарных ф-ий.
Непрерывность log, arcsin, arccos, arstg следует из определения непрерывности обратной ф-ии.
Df Элементарные ф-ии, полученные из основных элементарных ф-ий с помощью арифметических операций, взятых в конечном числе,********