4. Сходящиеся числовые последовательности. Теорема об ограниченности сходящейся числовой последовательности. Свойства сходящихся числовых последовательностей.
Последовательность, имеющая предел называется сходящейся, не имеющая его – расходящейся.
Определить
предел последовательности
.
(Ответ:
.)
Основные свойства сходящихся последовательностей
1.Если последовательность {xn} имеет предел, то он единственный.
2.Если последовательность {xn} сходится, то она ограничена.
Доказательство
Пусть
.
Зададим
.
Тогда
:
.
Известно,
что
,
поэтому
<1
.
Пусть
,
тогда
очевидно, что
.
5. Теорема о предельном переходе в неравенствах. Теоремы о промежуточной последовательности.
6. Монотонные последовательности. Теорема о сходимости монотонной ограниченной последовательности.
1)Последовательность
{xn}
называется возрастающей, если
.
2)
Последовательность {xn}
называется неубывающей, если
.
3)
Последовательность {xn}
называется убывающей, если
.
4)
Последовательность {xn}
называется невозрастающей, если
Если
последовательность
монотонна и ограничена, то она имеет
предел.
Д о к а з а т е л ь с т в о:
Пусть для определенности
-
возрастающая и ограничена сверху.
Зафиксируем
,
а так как
ограничена, то
и
.
Тогда в силу монотонности заданной
последовательности
в силу (1.2.1)
.
Поэтому
,
что по определению. означает
.
Аналогично теорема доказывается для случая, когда - убывающая и ограничена снизу.
7. Теорема о вложенных отрезках.
Пусть имеется множество отрезков, таких, что из любых двух один содержит другой. Тогда все эти отрезки имеют по крайней мере одну общую точку. (Краткая формулировка: Система вложенных отрезков всегда имеет общую точку.)
Док-во:
8. Число Эйлера (“e”).
Пусть
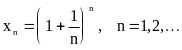
Покажем,
что последовательность
сходится.
Раскрывая скобки согласно правилу бинома Ньютона, получим
+
=
...+
.
При
переходе от
к
число слагаемых, которые все положительны,
возрастает, и кроме того, каждое слагаемое
увеличивается:
,
то
.
Далее, замечая, что
каждая из скобок вида
и
,
получим
.
В
левой части неравенства - бесконечно
убывающая геометрическая прогрессия
.
Следовательно,
.
Но последовательность монотонно возрастает и ограничена сверху, а значит, имеет предел, который обозначим буквой е.
9. Понятие функции, способы ее задания. Классификация функций.
Понятие функции
Пусть x и y – некоторые числовые множества. Если каждому элементу множества X единственным образом соответствует элемент множества Y, то это соответствие называется функцией.
Обозначение:
.
Здесь y – зависимая переменная, х – независимая переменная (аргумент)
X – обл. определения (существования) функции (D(f));
Y – множество значений функции (E(f)).
Способы задания функции
1.Аналитический
При аналитическом способе задания функция задается с помощью формул:
А) в явном виде
Функция
разрешена относительно y:
.
Б) в неявном виде
Функция
не разрешена относительно y:
.
При аналитическом способе функцию можно задать:
а) несколькими выражениями:
б) параметрически:
в) в полярной системе координат:
2. Табличный
3.Графический
Классификация элементарных функций
Основные элементарные функции
а)
тригонометрические:
;
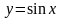б)
обратные тригонометрическим: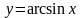
;
в)
степенная:
;
г)
показательная:
;
д)
логарифмическая:
.