1. Числовые последовательности. Ограниченные и неограниченные множества. Верхние и нижние грани множества.
Под числовой посл-тью х1, х2, х3,…, хn понимается функция хn = f(n) заданная на множестве натуральных чисел. Кратко обозначается {xn}, причем числа образующие данную посл-ть наз-ся ее эл-ми, а эл-т хn общим эл-том посл-ти . !Порядок следования эл-тов оч. важен, перестановка хотя бы 2-х эл-тов приводит к др. посл-ти. Пусть X – числовое множество.
А). Множество X ограниченно тогда и только тогда, когда X ограниченно сверху и снизу:
т.е.
.
В).
Множество X ограниченно сверху тогда и
только тогда, когда
С).
Множество X ограниченно снизу тогда и
только тогда, когда
D) Множество Х неограниченно тогда и только тогда, когда х>M
Любое ограниченное сверху (снизу) множество имеет бесконечно много верхних (нижних граней).
Естественно возникает вопрос о существовании наименьшей из верхних граней ограниченного сверху множества и наибольшей из нижних граней ограниченного снизу множества.
А). Число M называется точной верхней гранью, если оно является наименьшим из всех верхних граней.
Б). Число m называется точной нижней гранью, если оно является наибольшим из всех нижних граней.
Для
множества
указать точную верхнюю и точную нижнюю
грани.
Ответ:
;
.
2. Бесконечно малые и бесконечно большие последовательности. Свойства бесконечно малых последовательностей. Теорема связи между бесконечно большими и бесконечно малыми последовательностями.
Последовательность
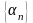называется
бесконечно малой, если для любого малого
положительного числа
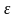можно
подобрать такой номер N,
что, начиная с этого номера (т.е. для всех
),
будет выполнено неравенство
<
.
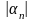Пример
б.м.п.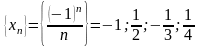
…
Св-ва б.м.п.:
1.
-б.м.п.
2.
-б.м.п.,
-
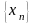огранич. посл-ть
-б.м.п.
3.
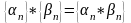-б.м.п.
4.
-б.м.п.,
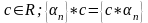
Последовательность
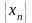наз-ся
полож. бесконечно большой, если для
любого большого числа M
найдется такой номер N,
что для всех n,
начиная с этого номера, выполняется
неравенство xn>M.
Пример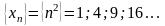
Последовательность наз-ся отриц. бесконечно большой, если для любого большого по модулю отриц. числа M найдется такой номер N, что для всех n, начиная с этого номера, выполняется неравенство xn<M.
Пример
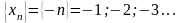
Связь
между б.м.п. и б.б.п.: Если
-б.б.п.
(все ее члены
0),
то посл-ть
-б.м.п.
Обратная формулировка также верна.
Док-во:
Пусть
-б.б.п.
Возьмем любое
>0
и положим
.
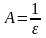Согласно опр-ю б.б.п. для А
сущ-ет номер N
такой, что при
n>N
будет
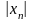>A.
Отсюда получаем,
что
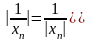для
всех n>N.
A
это значит, что
-б.м.п.
3. Предел числовой последовательности Теорема о единственности предела. Критерии Коши.
Число
а называется пределом числовой
последовательности {xn},
если для любого положительного числа
ε
существует номер N
такой, что при всех n>N
выполняется неравенство
.
Обозначение:
или
.
Геометрический смысл предела числовой последовательности
Число
a – предел последовательности xn,
если в любую окрестность числа а, начиная
с некоторого номера попадают все члены
последовательности
.
Теорема "Об единственности пределов" Посл-ть не может иметь больше одного предела.
Док-во
(от противного)
{xn}
имеет два разл. предела a и b (a
b).
.
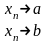По определению существует такое число
>0,
что
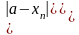Получается, что
,
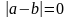т.е. a=b.
Для того, чтобы функция f (x) при x → a стремилась к конечному пределу A , необходимо и достаточно, чтобы функция α (x) = f (x) − A была бесконечно малой в точке a .
Доказательство. Необходимость. Если lim x→a f (x) = A , то
∀ε > 0 ∃δ > 0: ∀x ∈ Rδ (a) {a} ⇒ f (x) − A < ε .
Очевидно, что f (x) − A < ε ⇒ α (x) − 0 < ε . Откуда немедленно следует, что
lim x→a α (x) = 0 .
Достаточность. Если lim x→a f(x) = 0 , то
∀ε > 0 ∃δ > 0: ∀x ∈ Rδ (a) {a} ⇒ α (x) − 0 < ε .
Так как α (x) − 0 < ε ⇒ f (x) − A < ε , то это и означает, что lim x→a f (x) = A .
Доказанную теорему можно сформулировать иначе: функция f (x) при
x → a стремится к конечному пределу A тогда и только тогда, когда f (x)
равна сумме числа A и некоторой функции α (x) , бесконечно малой в точке a
f (x) = A + α (x).
(Критерий Коши). Для того, чтобы последовательность сходилась, необходимо и достаточно, чтобы она удовлетворяла условию Коши.
Последовательность
удовлетворяет условию Коши, если
.