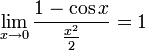- •1. Числовые последовательности. Ограниченные и неограниченные множества. Верхние и нижние грани множества.
- •2. Бесконечно малые и бесконечно большие последовательности. Свойства бесконечно малых последовательностей. Теорема связи между бесконечно большими и бесконечно малыми последовательностями.
- •3. Предел числовой последовательности Теорема о единственности предела. Критерии Коши.
- •4. Сходящиеся числовые последовательности. Теорема об ограниченности сходящейся числовой последовательности. Свойства сходящихся числовых последовательностей.
- •5. Теорема о предельном переходе в неравенствах. Теоремы о промежуточной последовательности.
- •6. Монотонные последовательности. Теорема о сходимости монотонной ограниченной последовательности.
- •7. Теорема о вложенных отрезках.
- •8. Число Эйлера (“e”).
- •9. Понятие функции, способы ее задания. Классификация функций.
- •10. Два определения предела функции в точке. Теорема об эквивалентности определений пределов функции в точке.
- •11.Теорема о пределе суммы, произведения, и частной функции. Предел функции на бесконечности. Теорема об ограниченности функции, имеющей предел.
- •12. Односторонние пределы. Теоремы о переходе к пределу в неравенствах.
- •13. Теорема о 1-м замечательном пределе.
- •14.Теоремы о 2-м замечательном пределе.
- •15. Бесконечно малые и бесконечно большие функции, сравнение бесконечно малых функций, эквивалентные бесконечно малые. Связь между бесконечно большими и бесконечно малыми
- •16. Непрерывность функции в точке. Примеры. Свойства непрерывных в точке функций. Теорема о непрерывности сложной функции.
- •17. Теорема о непрерывности обратной функции. Критерий непрерывности функции в точке. Односторонняя непрерывность.
- •18.Бесконечные пределы ф-ии.
- •19. Понятие непрерывности ф-ии.
- •20. Общие свойства ф-ии, непрерывной в точке.
- •Непрерывность и арифметические операции
- •Непрерывность сложной ф-ии.
- •21. Непрерывность ф-ии на множестве.
- •22. Характеристика точек разрыва ф-ии.
- •23. Односторонняя непрерывность ф-ии.
- •Свойства ф-й, непрерывных на отрезке
- •24. Дифференциальное счисление.
- •25. Определение призводной ф-ии в точке.
- •26. Степень ф-ии с вещественным показателем.
- •27. Геометрический смысл производной.
- •28. Дифференцируемость ф-ии.
- •29. Производная суммы, произведения, частного.
- •31. Производная от обратной ф-ии.
- •32. Производная от обратной ф-ии.
- •Производная от сложной ф-ии.
- •Односторонние производные.
- •33. Производная от параметрически заданной ф-ии.
- •34. Производные высших порядков.
- •35. Теоремы о дифф. Ф-ях.
- •36. Приложение производной к исследованию ф-ий.
- •37. Исследование ф-ии на выпуклость графика.
- •38. Асимптоты графика ф-ии.
- •Общая схема исследования ф-ий
- •39. Приложение производной к вычислению пределов.
- •40. Дифференциал ф-ии.
10. Два определения предела функции в точке. Теорема об эквивалентности определений пределов функции в точке.
Предел
функции в точке
 .
.
Определение (на языке последовательностей)
Пусть
функция f(x) определена на множестве X.
Пусть также заданы: последовательность
![]() причем
причем
![]() ,
,
а
также соответствующая последовательность
![]() причем
причем
![]()
![]() тогда
тогда
![]() .
.
Или:
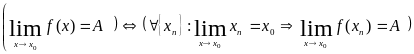 .
.
Определение
(предела функции в точке на языке
эпсилон-дельта (![]() ))
))
Число
A называется пределом функции f(x) в
точке![]() ,
если:
,
если:
![]() удовлетворяющих
неравенству, выполняется неравенство
удовлетворяющих
неравенству, выполняется неравенство
![]() .
.
Или:
![]() .
.
Оба определения предела функции эквивалентны.
11.Теорема о пределе суммы, произведения, и частной функции. Предел функции на бесконечности. Теорема об ограниченности функции, имеющей предел.
ТЕОРЕМА 1. Предел суммы двух функций при x стремящемся к a равен сумме пределов этих функций, то есть
![]()
ТЕОРЕМА 2. Предел произведения двух функций при x стремящемся к a равен произведению пределов этих функций, то есть
![]()
ТЕОРЕМА 3. Предел частного двух функций при x стремящемся к a равен частному пределов, если предел знаменателя отличен от нуля, то есть
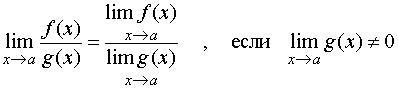
и равен плюс (минус) бесконечности, если предел знаменателя 0, а предел числителя конечен и отличен от нуля.
Пусть
ф-я
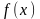 определена на бесконечном промежутке
определена на бесконечном промежутке
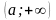
Число
А называется пределом ф-ии
при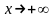 ,
если для любой положительной бесконечно
большой последовательности
(т.е.
,
если для любой положительной бесконечно
большой последовательности
(т.е.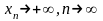 ) последовательность
) последовательность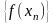 соответствующих значений ф-ии сходится
к А.
соответствующих значений ф-ии сходится
к А.
Пусть
задана числовая функция с неограниченной
сверху областью определения. Число
![]() называется
пределом функции f при
называется
пределом функции f при
![]() если
для любого числа ε>0
найдется такое число М>0, что для всех
значений х>М выполняется неравенство
если
для любого числа ε>0
найдется такое число М>0, что для всех
значений х>М выполняется неравенство
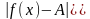
Пишут:
![]()
Число
называется
пределом функции f при
![]() если
для любого числа ε>0
найдется такое число М>0, что для всех
значений х>М выполняется неравенство
если
для любого числа ε>0
найдется такое число М>0, что для всех
значений х>М выполняется неравенство
Пишут:
![]()
об ограниченности функций, имеющих предел
Если
![]() ,
то существует некоторая проколотая
окрестность этой точки
,
то существует некоторая проколотая
окрестность этой точки
![]() ,
в которой функция ограничена.
,
в которой функция ограничена.
Доказательство
![]()
Пусть
![]()
![]() .
.
12. Односторонние пределы. Теоремы о переходе к пределу в неравенствах.
Односторонние пределы
Если
у любой сходящейся к точке
![]() последовательности
все ее элементы меньше
,
а соответствующая последовательность
последовательности
все ее элементы меньше
,
а соответствующая последовательность
![]() сходится к
сходится к
![]() ,
то число
называется левым пределом функции
,
то число
называется левым пределом функции
![]() .
.
Обозначение:
![]() .
.
Если
у любой сходящейся к
последовательности
![]() все ее элементы больше
,
а соответствующая последовательность
сходится к
все ее элементы больше
,
а соответствующая последовательность
сходится к
![]() ,
то число
называется правым пределом функции
f(x):
,
то число
называется правым пределом функции
f(x):
Обозначение:
![]() .
.
Утверждение.
Функция
![]() имеет предел в точке
тогда и только тогда, когда в этой точке
существуют пределы справа и слева и они
равны
имеет предел в точке
тогда и только тогда, когда в этой точке
существуют пределы справа и слева и они
равны
![]() .
.
13. Теорема о 1-м замечательном пределе.
![]()
Доказательство

Рассмотрим
односторонние пределы
![]() и
и
![]() и
докажем, что они равны 1.
и
докажем, что они равны 1.
Пусть
![]() .
Отложим этот угол на единичной окружности
(R = 1).
.
Отложим этот угол на единичной окружности
(R = 1).
Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.
Очевидно, что:
![]()
![]()
![]()
(из
![]() :
| LA | = tgx)
:
| LA | = tgx)
Подставляя в (1), получим:
![]()
Так
как при
![]() :
:
![]()
Умножаем на sinx:
![]()
Перейдём к пределу:
![]()
![]()
![]()
Найдём левый односторонний предел:
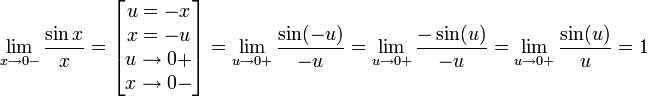
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.
Следствия
![]()
![]()
![]()