14.Теоремы о 2-м замечательном пределе.

Второй замечательный предел

Доказательство второго замечательного предела:

Доказательство второго замечательного предела для случая последовательности (т.е. для натуральных значений x) 

  Докажем вначале теорему для случая последовательности

По формуле бинома Ньютона:

Полагая , получим:

      (1)

Из данного равенства (1) следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число 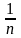убывет, поэтому величины возрастают. Поэтому последовательность — возрастающая, при этом

     (2).

Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу, правая часть увеличится, получим неравенство

Усилим полученное неравенство, заменим 3,4,5, …, стоящие в знаменателях дробей, числом 2:

.

Сумму в скобке найдем по формуле суммы членов геометрической прогрессии:

.

Поэтому       (3).

Итак, последовательность ограничена сверху, при этом выполняются неравенства (2) и (3):   .

Следовательно, на основании теоремы Вейерштрасса (критерий сходимости последовательности) последовательность монотонно возрастает и ограниченна, значит имеет предел, обозначаемый буквой e. Т.е.

Следствия

15. Бесконечно малые и бесконечно большие функции, сравнение бесконечно малых функций, эквивалентные бесконечно малые. Связь между бесконечно большими и бесконечно малыми

Бесконечно малые функции

– бесконечно малая функция, если .

Свойства бесконечно малых функций

.

. Сумма и произведение конечного числа бесконечно малых функций при является бесконечно малой функцией при .

. Произведение бесконечно малой функции на ограниченную функцию есть бесконечно малая функция.

– бесконечно большая функция при , если:

.

Замечание 1. Бесконечно большая функция не имеет предела при , но условно говорят: .

Замечание 2. Выражения вида называются неопределенностью.

Сравнение бесконечно малых и бесконечно больших функций

Рассмотрим функции и , заданные в проколотой окрестности точки ( ).

Определение

Если , то говорят, что эквивалентна при .

Определение Если и – бесконечно малые (бесконечно большие) функции при и ,то говорят, что они бесконечно малые (бесконечно большие) функции одного порядка.

Определение Если f(x) и g(x) – бесконечно малые (бесконечно большие) функции при и , то говорят, что – бесконечно малая функция более высокого порядка, чем .

( бесконечно большая функция менее высокого порядка, чем ).

Замечание 3. В случае бесконечно малых функций часто используют символ «о»: .

В примере 19.1.

Теорема 19.6. (замена функций эквивалентными при вычислении пределов)

Пусть при и определена в проколотой окрестности точки а( ). Тогда, если существует и существует , то существуют , и они равны предыдущим.

Доказательство

1). Пусть существует , тогда

.

2) .

16. Непрерывность функции в точке. Примеры. Свойства непрерывных в точке функций. Теорема о непрерывности сложной функции.

Функция определенная в некоторой окрестности точки , включая саму точку , называется непрерывной в этой точке, если

(20.1)

Замечание 1. Таким образом, согласно определению 20.1. предел функции и ее значение в точке равны.

Функция f(x) непрерывна в точке тогда и только тогда, когда для любой последовательности из некоторой окрестности точки , сходящейся к , соответствующая последовательность сходится к .

Преобразуем формулу (20.1):

.

Определение 20.4.

Функция f(x) называется непрерывной в точке , если ее приращение в этой точке является бесконечно малой функцией при

Замечание 2. Определения 20.1-20.4 эквивалентны.

Теорема 20.1.

Пусть функции и непрерывны в точке . Тогда , (если ) также непрерывны в этой точке.

Сложная функция

Определение 20.5

Пусть заданы функции : область определения функции f(x) содержит область значений функции (x).

Тогда определена функция называемая сложной функцией.

Теорема20.1.

Если непрерывна в точке , а непрерывна в точке , то непрерывна в точке .

Доказательство:

(в силу непрерывности функции).

Также в силу непрерывности функции имеем:

т.е. .

Теорема20.2 (об ограниченности непрерывных функций).

Если функция f(x) непрерывна в точке , то существует окрестность этой точки, на которой f(x) ограничена.

Доказательство:

.