1.Понятие множества. Конечные и бесконечные множества. Операции над

множествами. Актуально и потенциально бесконечные множества.

Представление множеств в компьютере.

Точного определения понятия "множество" в математике нет. Создатель теории множеств – немецкий математик Кантор. Mножество или совокупность – это собрание определенных и различных объектов нашей интуиции или интеллекта, мыслимое в качестве целого (по Кантору ).

Множество – совокупность элементов, объединённых каким-либо общим свойством.

Пример:

Множество S страниц в данной книге. Множество N натуральных чисел 1,2,3,... Множество P простых чисел 2,3,5,7,11,... Множество Z целых чисел: ...,-2,-1,0,1,2,... Множество R вещественных чисел. Множества А различных символов на этой странице.

Способы задания множества:

А) перечисление всех его элементов (элементы заключаются в фигурные скобки)

А= {1,5}

Б) с помощью характеристического свойства его элементов.

А= {х | х - чётное число}

Множество называется конечным, если оно не равномощно ни одному своему собственному подмножеству. Иначе - бесконечно. Мощность – количество элементов. Потенциальное бесконечное множество – множество, которое в каждый конечный момент времени конечно и содержит k элементов, однако, для таких множеств в любой следующий момент времени может добавится 1 элемент k+1.

Т.о. п. б. м. – в любой конечный момент времени конечно, но количество элементов заранее неизвестно. (пример: файл)

Операции над множествами:

• Объединение множеств A и B : AB x | xAxBили

Объединением множеств A и B называется множество C, состоящее из элементов, которые принадлежат хотя бы одному из множеств A, B.

• Пересечение множеств A и B : AB x | xA& xB& - и

Пересечением множеств A и B называется множество C, состоящее из элементов, которые принадлежат каждому из множеств A и B.

• Разность множеств A и B : A \ B x | xA& xB

Разностью множеств A и B называется множество C, состоящее из элементов множества A, которые не принадлежат множеству B.

• Симметрическая разность A и B : AB A\ BB \ A

Симметрической разностью множеств A и B называется множество C, состоящее из всех тех элементов, которые принадлежат только одному из множеств A, B.

• Дополнение множества A относительно U , где A U : A( с чертой) U \ A.

Дополнением к множеству A называется множество, состоящее из элементов универсума U, которые не принадлежат множеству A.

2. Понятие отношения. Примеры.

Декартово произведение множеств A и B – есть множество вида

AB <x, y>| xA, yB

Отношение – множество пар, удовлетворяющих каким-либо свойствам.

Бинарное отношение между элементами множеств A и B называется

любое подмножество декартова произведения R AB .

R={(a,b) | a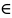 A,b B,a>b}

A={6,7,8}, B={5,6,7,8,9}, R={(6,5), (7,5), (7,6), (8,5), (8,6), (8,7)}

3. Отношение эквивалентности. Основная теорема. Фактор-множества.

Отношение эквивалентности – отношение(рефл., транз., симметр.)

1) Рефлексивность <x,x>є 

2) Симметричность <x,y>є  –><y,x>є 

3) Транзитивность <x,y>є , <y,z>є –><x,z>є 

Пример:

• А – множество прямых

Р= {(x,y) | x параллельна y}

• A= {1, 2, 3, 4, 5, 6, 7, 8, 9}

P= {(x, y) | x- y чётно}

Класс эквивалентности элемента х по эквивалентности R – множество:

=x/R= { y | (x,y) є R }

Множество классов эквивалентности элементов множества А по эквивалентности R называется фактор-множеством А по R. Обозначается А/R(А по модулю R).