Числовой ряд, основные определения и свойства.

Пусть задана последовательность действительных чисел {c_n}. Составим новую последовательность частичных сумм {S_n} следующим образом:

S₁=c₁ ; S₂=c₁+c₂ ; S_n=c₁+c₂+…+c_n, или по другому – частичной суммой элементов c_n называется сумма .

Числовым рядом называется последовательность частичных сумм ( или c₁+ c₂+…+ c_n). Сумма ряда называется предел этой последовательности . Если существует данный конечный предел, то ряд называется сходящимся (к сумме S), если конечный предел не существует, то ряд расходящийся. Числа c_n – элементы ряда, сумма - отрезок ряда, разность – остаток ряда. Далее обозначается .

Свойства рядов:

1. Удаление или добавление конечного множества элементов ряда не влияет на его поведение (сумма ряда при этом может измениться).

2. Арифметически свойства сходящихся рядов:

Связь между исходной последовательностью и последовательностью частичных сумм можно записать и как : И следовательно:

Необходимое условие сходимости.

Для сходимости ряда необходимо, чтобы . Это утверждение эквивалентно следующему : Если с_n не является бесконечно малой то ряд расходится.

Геометрическая прогрессия.

Частичная сумма -

Сумма прогрессии

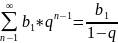
Критерий Коши сходимости числового ряда.

Для сходимости числового ряда необходимо и достаточно, чтобы последовательность его частных сумм сходилась в себе (или, что то же самое, отрезок ряда должен быть бесконечно малым):

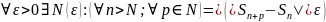
Положительные ряды. Критерии их сходимости.

Ряд называется положительным, если все элементы этого ряда неотрицательные. Ясно, что последовательность частичных сумм в этом случае неубывающая, а значит, для сходимости положительного ряда необходима и достаточна ограниченность последовательности его частичных сумм. Частичные суммы сходящегося положительного ряда не превосходят его суммы.

Признак сравнения положительных рядов.

1. Пусть при достаточно больших номерах .

Тогда .

2. Пусть существует конечный или бесконечный предел .

Тогда .

Следствие – если бесконечно малые a_n, b_n такие, что a_n=O(b_n), то поведение рядов одинаково.

3. Пусть при достаточно больших номерах a_n, b_n>0 , тогда

Итак, сходится при . Такой ряд называется обобщенным гармоническим рядом.

Признак Даламбера, достаточный признак Коши, признак Коши-Адамара для положительных рядов.

Признак Даламбера.

Если при достаточно больших номерах величина , то ряд сходится (при обратном расходится).

Доказательство. Пусть условия имеют место при всех номерах. Тогда в первом случае . Мажорирующий ряд состоит из элементов геометрической прогрессии со знаменателем q. По первому признаку сравнения, ряд сходится. Во втором случае ряд расходится.

Признак в предельной форме.

Если существует конечный или бесконечный предел , то ряд расходится (сходится).

Достаточный признак Коши.

Если при достаточно больших номерах величина , то ряд сходится (расходится).

Доказательство. В первом случае имеем: , мажорирующий ряд – снова геометрическая прогрессия, во втором – , не является бесконечно малой.

Признак в предельной форме.

Если существует конечный или бесконечный предел 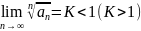, то ряд сходится (расходится).

Признак Коши-Адамара.

Если конечный или бесконечный верхний предел , то ряд сходится (расходится).

Доказательство. В первом случае выберем число . Числа K_n<q<1 при достаточно больших номерах. По достаточному признаку Коши, ряд сходится. Во втором случае есть подпоследовательность сходящаяся к верхнему пределу K > 1. Значит, при достаточно больших номерах р числа , последовательность a_n не является бесконечно малой, ряд расходится.

Признак Раабе.

Если при достаточно больших номерах величина то ряд сходится (расходится).

Предельная форма.

Интеграл 1-го рода, понятие, свойства, сходимость.

Пусть функция f(x) определена при , имеет определенные интегралы 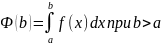. Если существует конечный или бесконечный предел , то он называется несобственным интегралом 1-го рода. Пусть функция f(x)>0 всюду. Тогда функция Ф(b) – возрастающая, и этот предел существует. Если он конечный, то говорят, что интеграл сходится. В противном случае – расходится. В любом случае .

Для сходимости интеграла необходима и достаточна ограниченность функции Ф, для расходимости – ограниченность.

Если известна первообразная F для функции f, то

Интегральный признак сходимости положительного ряда

Пусть непрерывная невозрастающая функ. f(x)>0 определена при . Тогда поведение ряда одинаково.

Доказательство. Достаточно доказать, что из сходимости ряда следует сходимость интеграла, и наоборот. Сходимость интеграла доказывается через теорему о среднем. Так же то, что сама функция увеличивается имеем то, что она ограничена сверху, следовательно сходится к конечному пределу, следовательно интеграл сходится.

Абсолютная сходимость рядов.

Ряд называется абсолютно сходящимся, если сходится ряд .

Для абсолютной сходимости ряда, очевидно, необходима и достаточна ограниченность последовательности его частичных сумм . Из абсолютной сходимости следует и обычная сходимость, но наоборот не действует.

Признаки сравнения абсолютно сходящихся рядов.

1. Если при достаточно больших номерах 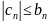и ряд сходится, то ряд сходится абсолютно.

2. Если существует конечный предел абсолютно сходится, то ряд тоже сходится абсолютно. Если значение c>0, то верно и обратное утверждение.

3. Если ряд абсолютно сходится и при достаточно больших номерах , то ряд абсолютно сходится.

Достаточные признаки абсолютной сходимости.

Признак Даламбера.

Если существует конечный или бесконечный предел , то ряд абсолютно сходится (расходится).

Признак Коши.

Если существует конечный или бесконечный предел , то ряд абсолютно сходится (расходится).

Признак Коши-Адамара.

Если существует конечный или бесконечный предел , то ряд абсолютно сходится (расходится).

Признак Раабе.

Если существует конечный или бесконечный предел , то ряд абсолютно сходится.

Интегральный признак.

Если непрерывная возрастающая функция f(x)>0 определена при a>0, значение , интеграл сходится, то ряд сходится абсолютно.

Условная сходимость.

Знакопеременный ряд (он же просто ряд) называют сходящимся условно, если он сходится, а ряд расходится.

Признак Лейбница.

Если последовательность элементов b_n монотонно стремится к нулю, то есть , то ряд сходится.

Доказательство. Берем знакочередующийся ряд(самый простой, в котором тупо плюсы и минусы между слагаемыми чередуются). Рассмотрим частичные суммы S_2n+1 данного ряда. Сгруппировав слагаемые особым образом, имеем каждая из скобок заведомо больше нуля и положительна, а значит данные частичные суммы не убывают и ограничены сверху, а значит, сходятся к некоторому значению, которые мы обозначим S. Для остальных частичных сумм, ввиду бесконечной малости элементов, имеем . Итак, последовательность частичных сумм, а значит и ряд, сходятся.

Тождество Абеля.

Рассмотрим не только знакочередующиеся ряды. Предварительно рассмотрим одно преобразование сумм следующего вида: . Введем в рассмотрение частичные суммы элементов b_k: .Теперь выразим элементы b_k через данные частичные суммы и подставим их в S_n: . Раскроем скобки в полученной сумме и сгруппируем слагаемые, вынося за скобки B_k. Окончательно имеем:

Такое преобразование сумм называется преобразованием Абеля ; оно является аналогом формулы интегрирования по частям.

Признак Дирихле.

Пусть для двух последовательностей элементов a_n и b_n выполняются следующие условия:

- последовательность частичных сумм 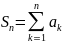ограничена ;

- при достаточно больших номерах последовательность ;

Тогда ряд 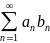сходится.

Доказательство. Из 2-го условия следует, что при достаточно больших номерах . Обозначим верхнюю границу частичных сумм . Чтобы установить сходимость нашего ряда при данных условиях, проверим выполнение условий критерия Коши. Применим к оценке отрезка ряда при m>n>N(E) тождество Абеля и неравенство треугольника, и получим, что отрезок ряда произведений бесконечно мал, следовательно, искомый ряд сходится.

Теорема Дирихле-Абеля.

Пусть для двух последовательностей элементов a_n и b_n выполняются следующие условия:

- ряд 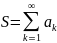сходится

- при достаточно больших номерах последовательность

Тогда ряд сходится.

Доказательство. Сходимость ряда означает, что по определению, сходимость последовательности частичных сумм и, следовательно, ее ограниченность. По признаку Дирихле ряд сходится.

Признак Абеля.

Пусть для двух последовательностей элементов a_n и b_n выполняются следующие условия:

- ряд сходится

- при достаточно больших номерах последовательность b_n ограничена и монотонна

Тогда ряд сходится.

Доказательство. Монотонная ограниченная переменная , поэтому монотонно. Тогда исходный ряд можно представить в виде суммы двух сходящихся рядов: .

Перестановка положительных и абсолютно сходящихся рядов.

Сходящийся ряд допускает перестановку, если результатом любой перестановки его элементов является ряд, сходящийся к сумме S.

Рассмотрим сначала перестановку относительно положительных рядов.

Пусть ряд сходится к сумме А, а ряд получен в результате перестановки. Зафиксируем номер n. В частичной сумме элементов 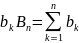элементам b_k соответствуют некоторые элементы первого ряда. Среди номеров найдем максимальный m=max{n_k}, . Поскольку частичные суммы содержат все элементы частичных сумм и, возможно, еще какие-то слагаемые, то . Тогда последовательность частичных сумм положительного ряда ограничена сверху, а значит сходится к некоторой сумме . В силу взаимности перестановки (обратно от ряда к ряду ), имеем еще одно неравенство: , но тогда . Тем самым доказана возможность перестановки.

Теперь рассмотрим абсолютно сходящиеся ряды.

Покажем, что абсолютно сходящийся ряд равен разности сходящихся положительных рядов. Рассмотрим ряд . Введем в рассмотрение две неотрицательные последовательности a_n, b_n (положительная и отрицательная части ряда):

Обратим внимание на два последних неравенства. Согласно признаку сравнения положительных рядов, ряд сходится к некоторой сумме, обозначим ее А. Аналогично, ряд сходится к некоторой сумме В. Так как сходящиеся ряды обладают арифметическими свойствами, то . То же происходит и с рядами, полученными в результате перестановки ряда элементов c_n , так как положительные ряды допускают перестановку.

Теорема Римана[1].

Если ряд сходится условно, то, каково бы ни было наперед взятое число L конечное или бесконечное, можно так переставить члены ряда, чтобы преобразованный ряд сходился к L.

Умножение абсолютно сходящихся рядов.

Пусть заданы сходящиеся ряды . Все произведения a_i*b_k выстроим произвольным образом в последовательность . Ряд называется рядом произведения .

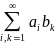Теорема.

Если ряды абсолютно сходятся и имеют суммы А, В, то ряд произведений абсолютно сходится и имеем сумму А*В,

Функциональные последовательности и ряды.

Определение. Пусть задано некоторое множество Х и каждому числу ставится в соответствие по определенному закону некоторая функция f_n(x), заданная на множестве Х, тогда будем говорить, что задана функциональная последовательность {f_n(x)}. Функции f_n(x) являются элементами последовательности, множество Х – область определения последовательности.

Определение. Множество всех точек х, на которых сходится функциональная последовательность {f_n(x)}, называется областью сходимости. Функцию будем называть предельной функцией.

Определение. Пусть на некотором множестве Х задана функциональная последовательность {f_n(x)}. Составим новую последовательность частичных сумм {S_n(x)} следующим образом : .

Получившуюся последовательность будем называть функциональным рядом и обозначить . Функции f_n(x) – элементы ряда, суммы вида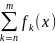 - отрезок ряда. Далее для краткости обозначать буду . Как и в случае с числовыми рядами и последовательностями, для функциональных рядов и последовательностей справедливы общие понятия, связанные со сходимостью и абсолютной сходимостью и т.д.