Дросселирование.

Дросселирование – процесс движения паров, жидкостей и газов через внезапное сужение(местное сопротивление).

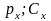
Для быстро протекающего процесса можно теплотой внешнего теплообмена пренебречь, то есть , также , .

Первое начало термодинамики: , следовательно, , или , то есть процесс изоэнтальпийный, но он реальный, то есть протекает с необратимыми потерями давления.

Явление изменения температуры газа или жидкости при адиабатном дросселировании называется эффектом Джоуля – Томсона .

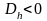Для характеристики дроссельного процесса вводится коэффициент Джоуля-Томпсона: , который можно найти по следующей формуле . Если , то . Если , то . Если , то .

Дросселирование является изоэнтальпийным процессом, при котором .

Для идеального газа , тогда , следовательно .

Переход через критическую скорость (сопло Лаваля).

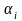- угол раскрытия канала.

Начальные параметры: , , .

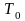Параметры среды: , , .

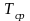Можно поставить две задачи:

1. Найти линейную скорость, массовую скорость и массовый расход, при известной геометрии аппарата.

2. Найти геометрию аппарата, при известном массовом расходе.

Решаем вторую задачу.

Сравнивая величину с , получим три варианта:

1. Докритический режим, .

2. Критический режим: .

3. Закритический режим: .

Нужно найти площади сечений: , , .

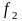Уравнение неразрывности: . Подставляя в это уравнение массовые скорости, можно найти площади сечений, но для каждого случая нужно знать величину , то есть нужно с помощью уравнений процессов ( и ) найти давления , , . Зная площади сечений можно найти характеристические размеры сечений.

14-15. Идеальные циклы Карно, термодинамический КПД цикла.

Цикл Карно́ — идеальный термодинамический цикл. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно. Одним из важных свойств цикла Карно является его обратимость: он может быть проведён как в прямом, так и в обратном направлении, при этом энтропия адиабатически изолированной (без теплообмена с окружающей средой) системы не меняется.

Цикл Карно состоит из четырёх стадий:

И зотермическое расширение (на рисунке — процесс 1→2). В начале процесса рабочее тело имеет температуру TH, то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты QH. При этом объём рабочего тела увеличивается. Адиабатическое (изоэнтропическое) расширение (на рисунке — процесс 2→3). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника. Изотермическое сжатие (на рисунке — процесс 3→4). Рабочее тело, имеющее к тому времени температуру TX, приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплоты QX. Адиабатическое (изоэнтропическое) сжатие (на рисунке — процесс Г→А). Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя. При изотермических процессах температура остаётся постоянной, при адиабатических отсутствует теплообмен, а значит, сохраняется энтропия (поскольку , при δQ = 0).

Поэтому цикл Карно удобно представить в координатах T и S (температура и энтропия). КПД тепловой машины Карно

Количество теплоты, полученное рабочим телом от нагревателя при изотермическом расширении, равно Аналогично, при изотермическом сжатии рабочее тело отдало холодильнику 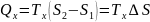. Отсюда коэффициент полезного действия тепловой машины Карно равен . Из последнего выражения видно, что КПД тепловой машины Карно зависит только от температур нагревателя и холодильника. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм. Можно показать, что КПД любой тепловой машины, работающей по циклу, отличному от цикла Карно, будет меньше КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника.