10. Изотермический процесс — термодинамический процесс, происходящий в физической системе при постоянной температуре.

Несколько изотерм для идеального газа нa p-V диаграмме

В идеальном газе при изотермическом процессе произведение давления на объём постоянно (закон Бойля-Мариотта). Изотермы идеального газа в координатах p,V — гиперболы, расположенные на графике тем выше, чем выше температура, при которой происходит процесс (см. рисунок).

При изотермическом процессе системе, вообще говоря, сообщается определённое количество теплоты (или она отдаёт теплоту) и совершается внешняя работа. Альтернативный процесс, при котором теплообмен с окружающей средой отсутствует (термодинамическая система находится в энергетическом равновесии — система не поглощает и не выделяет тепло), называется адиабатическим процессом.

Работа, совершенная идеальным газом в изотермическом процессе, равна , где  — число частиц газа,  — температура, и  — объём газа в начале и конце процесса,  — постоянная Больцмана .

В твёрдом теле и большинстве жидкостей изотермические процессы очень мало изменяют объём тела, если только не происходит фазовый переход.

Первый закон термодинамики для изотермического процесса в идеальном газе записывается в виде:

   

Адиабатический процесс — термодинамический процесс в макроскопической системе, при котором система не получает и не отдаёт тепловой энергии.

Для адиабатического процесса первое начало термодинамики в силу отсутствия теплообмена (ΔQ = 0) системы со средой имеет вид

где:

• — изменение внутренней энергии тела,

• — работа, совершаемая системой

• — теплота, полученная системой

Основное уравнение термодинамики применительно к адиабатическому процессу записывается в дифференциалах как

,

где — дифференциальное выражение для работы, a_i — внешние параметры, A_i — соответствующие им внутренние параметры. В частном случае, когда работа совершается через изменение объёма

, где p — давление.

Энтропия системы в адиабатическом процессе не меняется:

.

11. Изохорный процесс. (V=const)

Изобарный процесс. (Р=const)

Изотермический процесс. (T=const)

Изоэнтропийный процесс (Q=const)

Адиабатный процесс(ΔQ = 0)

график адиабаты (жирная линия) на диаграмме для газа. p — давление газа; V — объём.

13. Истечение паров, жидкостей и газов.

Процесс истечения – процесс переноса вещества из области с одним давлением в область с другим.

Действительный процесс истечения характеризуется необратимыми потерями и неравномерностью распределения скоростей в потоке. В теории истечение рассматривается, как обратимый процесс, а переход к реальным характеристикам осуществляется с помощью двух коэффициентов: коэффициента скорости - и коэффициента расхода - , причём эти коэффициенты определяются экспериментальным путём. Оба коэффициента показывают различия между теоретическими и действительными величинами.

Нас интересуют следующие величины:

1. Линейная скорость - , .

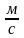2. Массовая скорость - , .

3. Массовый расход - , .

Задача решается на базе следующих уравнений:

1. Первое начало термодинамики: .

2. Уравнение процесса:

   1. Политропный процесс: .

   2. Адиабатный процесс: .

3. Уравнение неразрывности в интегральном виде: .

4. Уравнение состояние.

Основные соотношения процесса истечения.

Уравнение распределения потенциальной работы:

.

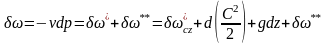Так как рассматриваются обратимые потери, то .

Так как рассматривается чистое движение, то .

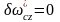Следовательно: .

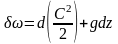Так как рассматриваются короткие каналы, то , .

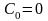Выражение для линейной скорости: .

Выражение для массовой скорости: .

Выражение для массового расхода: .

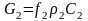Основные исходные соотношения.

Уравнение для линейной скорости: .

Уравнение для массовой скорости: .

Уравнение для массового расхода: .

Истечение несжимаемой (капельной) жидкости.

Условия не сжимаемости жидкости: , .

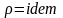Рассматриваем изохорный процесс. Потенциальную работу можно найти по следующей формуле: .

Подставив это в уравнение для линейной скорости, получим: .

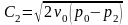Графическое представление зависимости скорости то перепада давления:

Подставив это в уравнение для массовой скорости, получим: .

Подставив это в уравнение для массового расхода, получим: .

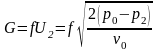Действительная линейная скорость отличается от теоретической, поэтому вводят коэффициент скорости , где - действительная линейная скорость, - теоретическая линейная скорость. Поэтому действительную линейную скорость можно найти по формуле: .

П ри течении жидкости в трубе с переменным сечением наблюдается отрыв струи от стенок и площадь сечения течения становится меньше площади сечения трубопровода. В связи с этим вводят коэффициент сжатия струи , при этом он лежит в пределах от 0.6 до 1. Если профиль канала параболический, то .

Действительный массовый расход можно найти по формуле: , где - коэффициент расхода.