1.03 Количество информации как мера уменьшения.

Информатика. Лекция «Количество информации как мера уменьшения неопределённости знаний»

ЛЕКЦИЯ

Тема: Количество информации как мера уменьшения неопределённости знаний

Алфавитный подход к определению количества информации

План:

1. Количество информации как мера уменьшения неопределённости знаний

2. Алфавитный подход к определению количества информации

1. Количество информации как мера уменьшения неопределённости знаний

Информация и знания. Человек получает информацию из окружающего мира с помощью органов чувств, анализи­рует ее и выявляет существенные закономерности с помо­щью мышления, хранит полученную информацию в памя­ти. Процесс систематического научного познания окружающего мира приводит к накоплению информации в форме знаний (фактов, научных теорий и так далее). Таким образом, с точки зрения процесса познания информация мо­жет рассматриваться как знания.

Процесс познания можно наглядно изобразить в виде рас­ширяющегося круга знания (такой способ придумали ещё древние греки). Вне этого круга лежит область незнания, а окружность является границей между знанием и незнанием. Парадокс состоит в том, что чем большим объемом знаний обладает человек (чем шире круг знаний), тем больше он ощущает недостаток знаний (тем больше граница нашего не­знания, мерой которого в этой модели является длиной окружности) — рис. 1.

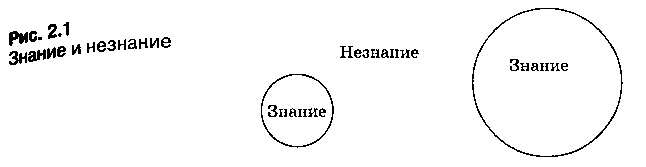
Рис. 1. Знание и незнание

Так, объем знаний выпускника школы гораздо больше, объем знаний первоклассника, однако и граница его незнания существенно больше. Действительно, первоклассник ничего не знает о законах физики и поэтому не осознает не­достаточности своих знаний, тогда как выпускник школы при подготовке к экзаменам по физике может обнаружить, что существуют физические законы, которые он не знает или не понимает.

Информацию, которую получает человек, можно считать мерой уменьшения неопределенности знаний. Если некото­рое сообщение приводит к уменьшению неопределенности наших знаний, то можно говорить, что такое сообщение со­держит информацию.

Например, после сдачи экзамена по информатике вы му­чаетесь неопределенностью, вы не знаете, какую оценку по­лучили. Наконец, экзаменационная комиссия объявляет ре­зультаты экзамена, и вы получаете сообщение, которое приносит полную определенность, теперь вы знаете свою оценку. Происходит переход от незнания к полному зна­нию, значит, сообщение экзаменационной комиссии содер­жит информацию.

Уменьшение неопределенности знаний.

Получение информации можно связать с уменьшением неопределённости знания. Это позволяет количественно измерять информацию, что чрезвычайно важно для информатики.

Рассмотрим вопрос об определении количе­ства информации более подробно на конкретных примерах.

Пример.

Дано. Пусть у нас имеется монета, которую мы бросаем на ровную поверхность. С равной вероятностью произойдет одно из двух возможных событий — монета окажется в одном из двух положений: «орел» или «решка».

Решение. Можно говорить, что события равновероятны, если при возрастающем числе опытов количества выпадений «орла» и «решки» постепенно сближаются. Например, если мы бросим монету 10 раз, то «орел» может выпасть 7 раз, а «решка» — 3 раза, если бросим монету 100 раз, то «орел» может выпасть 60 раз, а «решка» — 40 раз, если бросим монету 1000 раз, то «орёл» может выпасть 520 раз, а «решка» — 480 и так далее.

В итоге при очень большой серии опытов количества выпадений «орла» и «решки» практически сравняются.

Перед броском существует неопределенность наших знаний (возможны два события), и, как упадет монета, предсказать невозможно. После броска наступает полная определенность, так как мы видим (получаем зрительное сообщение) что монета в данный момент находится в определенном положении (например, «орел»). Это сообщение приводит к уменьшению неопределенности наших знаний в два раза, так как до броска мы имели два вероятных события, а после броска — только одно, то есть в два раза меньше (рис. 2.)

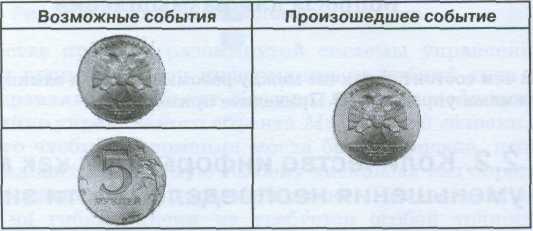
Рис. 2. Возможные и произошедшие события

В окружающей действительности достаточно часто встре­чаются ситуации, когда может произойти некоторое количе­ство равновероятных событий. Так, при бросании равносто­ронней четырехгранной пирамиды существуют 4 равновероятных события, а при бросании шестигранного иг­рального кубика — 6 равновероятных событий.

Чем больше количество возможных событий, тем больше начальная неопределенность и соответственно тем большее количество информации будет содержать сообщение о резуль­татах опыта.

Единицы измерения количества информации.

Для количественного выражения любой величины необходимо опре­делить единицу измерения. Так, для измерения длины в качестве единицы выбран метр, для измерения массы - килограмм и так далее. Аналогично, для определения коли­чества информации необходимо ввести единицу измерения.

За единицу количества информации принимается такое количество информации, которое содержит сообщение, уменьшающее неопределенность в два раза. Такая единица названа «бит».

Бит – это двоичный разряд, который может принимать значение 0 или 1.

1 бит – это наименьшая единица измерения информации.

Если вернуться к опыту с бросанием монеты, то здесь неопределенность как раз уменьшается в два раза и, следова­тельно, полученное количество информации равно 1 биту.

Байт – это восемь подряд записанных битов. В информатике это наиболее употребляемая единица измерения информации, причём,

1 байт = 2³ битов = 8 битов.

Пример. Одним байтом можно закодировать значение одного символа из 256 возможных. То есть одна буква, или цифра, или знак препинания, или другой символ и даже пробел – это 1 байт информации. Например, слово «информация» содержит 10 байт информации, а в битах это будет 10 · 8 = 80 бит.

В информатике система образования кратных единиц из­мерения количества информации несколько отличается от принятых в большинстве наук. Традиционны метрические системы единиц, например Международная система единиц (СИ)¹, в качестве множителей кратных единиц используют коэффициент 10ⁿ, где п = 3, 6, 9 и так далее, что соответствует десятичным приставкам Кило (10³), Мега (10⁶⁾, Гига (10⁹⁾ и так далее.

Компьютер оперирует числами не в десятичной, а в дво­ичной системе счисления, поэтому в кратных единицах из­мерения количества информации используется коэффици­ент 2ⁿ.

Так, кратные байту единицы измерения количества информации вводятся следующим образом:

1 Кбайт = 2¹⁰ байт = 1024 байт;

1 Мбайт = 2¹⁰ Кбайт = 1024 Кбайт;

1 Гбайт = 2¹⁰ Мбайт = 1024 Мбайт.

Пример. Если на странице учебника помещается примерно 50 строк, а в каждой строке примерно 60 символов, то страница учебника, полностью заполненная текстом, имеет информационный объем 3 000 байт (около 3 Кб). Если в учебнике 250 страниц, то его объем информации будет равен 750 Кб.

Количество возможных событий и количество информа­ции.

Существует формула, которая связывает между собой количество возможных событий N и количество информа­ции I:

N=2^I (1)

По этой формуле можно легко определить количество возможных событий, если известно количество информа­ции.

Например, если мы получили 4 бита информации, то количество возможных событий составляло:

N = 2⁴ = 16.

Наоборот, для определения количества информации, если известно количество событий, необходимо решить показательное уравнение относительно I.

Например, в игре «Крести-нолики» на поле 8 x 8 перед первым ходом существует 64 возможных события (64 различных варианта расположения «крестика»), тогда уравнение принимает вид: 64 = 2^I.

Так как 64 = 2⁶, то получим: 2⁶ = 2^I.

Таким образом, I = 6 битов, то есть количество информации, полученное вторым игроком после первого хода перво­го игрока, составляет 6 битов.

2. Алфавитный подход к определению количества информации

При определении количества информации на основе уменьшения неопределенности наших знаний мы рассмат­риваем информацию с точки зрения содержания, ее понят­ности и новизны для человека. С этой точки зрения в опы­те по бросанию монеты одинаковое количество информации содержится и в зрительном образе упавшей монеты, и в коротком сообщении «Орел», и в длинной фразе «Монета упала на поверхность земли той стороной вверх, на которой изображен орел».

Однако, при хранении и передаче информации с помощью технических устройств целесообразно отвлечься от содержания информации и рассматривать ее как последовательность знаков (букв, цифр, кодов цветов точек изображения и так далее).

Набор символов знаковой системы (алфавит) можно рассматривать как различные возможные состояния (события). Тогда, если считать, что появление символов в сообщении равновероятно, по формуле (1) можно рассчитать, какое количество информации несет каждый символ.

Так, в русском алфавите, если не использовать букву ё, количество событий (букв) будет равно 32. Тогда: 32 = 2^I, откуда I = 5 битов.

Каждый символ несет 5 битов информации (его инфор­мационная емкость равна 5 битов). Количество информа­ции в сообщении (I_с) можно подсчитать, умножив количество информации, которое несет один символ (I), на количество символов (K) в сообщении:

I_с = I × K. (2)

Количество информации, которое содержит со­общение, закодированное с помощью знаковой системы, равно количеству информации, которое несет один знак, умноженному на количество зна­ков.

Формула Шеннона

Существует множество ситуаций, когда возможные события имеют различные вероятности реализации. Например, если монета несимметрична (одна сторона тяжелее другой), то при ее бросании вероятности выпадения «орла» и «решки» будут различаться.

Формулу для вычисления количества информации в случае различных вероятностей событий предложил К. Шеннон в 1948 году. В этом случае количество информации определяется по формуле:

, (3)

где I — количество информации;

N — количество возможных событий;

р_i — вероятность выбора i-го события.

Для частного, но широко распространенного и рассмот­ренного выше случая, когда события равновероятны (р_i = 1/N), величину количества информации I можно рас­считать по формуле (формула Хартли):

(4)

Например, пусть при бросании несимметричной четырех­гранной пирамидки вероятности отдельных событий будут равны:

Тогда количество информации, которое мы получим после реализации одного из них, можно рассчитать по формуле (3):

I = - (1/2*log₂1/2 + 1/4*log₂1/4 + 1/8*log₂1/8 + 1/8*log₂1/8) битов =

= (1/2*log₂2 + 1/4*log₂4 + 1/8*log₂8 + 1/8*log₂8) битов =

= (1/2 + 2/4 + 3/8 + 3/8) битов = 14/8 битов = 1,75 бита.

Этот подход к определению количества информации на­зывается вероятностным.

При бросании симметричной четырехгранной пирамид­ки вероятности отдельных событий равны между собой:

Количество информации, которую мы получим после бросания симметричной пирамидки, можно рассчитать по формуле (4):

Таким образом, при бросании симметричной пирамид­ки, когда события равновероятны, мы получим большее ко­личество информации (2 бита), чем при бросании несим­метричной пирамидки, когда события неравновероятны (1,75 бита).

Количество информации, которую мы получаем, достигает максимального значения, если собы­тия равновероятны.

ЗНАТЬ

В технике (теория кодирования и передачи сообщений) под количеством информации понимают количество кодируемых, передаваемых или хранимых символов.

Бит — двоичный знак двоичного алфавита {0, 1}.

Бит — минимальная единица измерения информации.

Байт — это восьмиразрядный двоичный код, с помощью которого можно представить один символ.

Байт — единица количества информации в системе СИ.

Единицы измерения информации в вычислительной технике

1 бит	минимальная единица измерения информации
1 байт	= 8 битов
1 Кб (килобайт)	= 210байтов = 1024 байта ≈ 1 тысяча байтов
1 Мб (мегабайт)	= 210 Кб = 220 байтов ≈ 1 миллион байтов
1 Гб (гигабайт)	= 210 Мб = 230 байтов ≈ 1 миллиард байтов

Информационный объем сообщения (информационная емкость сообщения) — количество информации в сообщении, измеренное в битах, байтах или производных единицах (килобайтах, мегабайтах и так далее).

В теории информации количеством информации называют числовую характеристику сигнала, которая не зависит от его формы и содержания и характеризует уменьшение неопределенности после получения сообщения в виде данного сигнала. В этом случае количество информации зависит от вероятности получения сообщения о том или ином событии.

Для абсолютно достоверного события (событие обязательно произойдет, поэтому его вероятность равна 1) количество информации в сообщении о нем равно 0. Чем невероятнее событие, тем большее количество информации несет сообщение о нем. Лишь при равновероятных ответах ответ «да» или «нет» несет один бит информации.

Количество информации при вероятностном подходе можно вычислить, пользуясь следующими формулами.

1. Формула Хартли:

I = log ₂ N или 2^I = N,

где N — количество равновероятных событий (число возможных выборов), i — количество информации.

2. Модифицированная формула Хартли:

I = log ₂ (1/p) = - log ₂ p ,

где р — вероятность наступления каждого из N возможных равновероятных событий.

3. Формула Шеннона:

,

где I — количество информации, приходящееся на один символ алфавита;

N — количество возможных событий;

р_i — вероятность выбора i-го события.

Контрольные вопросы

1. Какие существуют единицы измерения информации?

2. Что является наименьшей единицей измерения информации?

3. Наиболее употребляемая единица измерения информации.

4. Как зависит количество информации от количества возможных событий?

5. В каком случае количество информации, полученной о событии, достигает максимального значения?

6. Почему количество информации в сообщении удобнее оценивать не по степени увеличения знания об объекте, а по степени уменьшения неопределённости наших знаний о нём?

7. Как определяется единица измерения количества информации?

1 СИ (SI, фр. Système International d’Unités) – международная система единиц, современный вариант метрической системы. СИ является наиболее широко используемой системой единиц в мире, как в повседневной жизни, так и в науке и технике. В настоящее время СИ принята в качестве законной системы единиц большинством стран мира и почти всегда используется в области науки, даже в тех странах, в которых в повседневной жизни используются традиционные единицы.

6

Авторы: Родионова И.В., Короткова Т.В.