Законы Кеплера. Закон всемирного тяготения К началу XVII века большинство ученых было уверено в справедливости гелиоцентрической системы мира. И. Кеплер (1571-1630), обработав и уточнив результаты многочисленных наблюдений датского астронома Т. Браге (1546-1601), изложил законы движения планет:  1. Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце.  2. Радиус-вектор планеты за равные промежутки времени описывает одинаковые площади.  3. Квадраты периодов обращения планет вокруг Солнца относятся как кубы боль¬ших полуосей их орбит.  Вскоре И. Ньютон, при исследовании движения небесных тел, используя законы Кеплера и основные законы динамики открыл всеобщий закон всемирного тяготения: между любыми двумя материальными точками действует сила взаимного притяжения, прямо пропорциональная произведению масс этих точек (m1 и m2) и обратно пропорциональная квадрату расстояния между ними (r2):   (1)  Эта сила называется гравитационной (или силой всемирного тяготения). Силы тяготения всегда являются силами притяжения и направлены вдоль прямой, проходящей через взаимодействующие тела. Коэффициент пропорциональности G называется гравитационной постоянной.  Закон всемирного тяготения установлен для тел, которые мы принимаем за материальные точки, т. е. для такие тела, у которых размеры малы по сравнению с расстоянием между ними. В случае, если размеры взаимодействующих тел сравнимы с расстоянием между ними, то эти тела следует разбить на малые элементы, используя формулу (1) найти силы притяжения между всеми попарно взятыми элементами и после этого геометрически их сложить (проинтегрировать), что есть достаточно сложная математическая задача.  Значение G, которая дается в таблицах фундаментальных физических постоянных, принимается равным 6,6720•10-11 Н•м/кг2, т. е. два точечных тела массой по 1 кг каждое, находящиеся на расстоянии 1 м друг от друга, притягиваются с силой 6,6720•10-11 H. Очень малая величина G показывает, что сила гравитационного взаимодействия может иметь существенное значение только в случае больших масс.

Первый закон Кеплера (закон эллипсов)

Первый закон Кеплера.

Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце.

Форма эллипса и степень его сходства с окружностью характеризуется отношением  , где c — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), a — большая полуось. Величина e называется эксцентриситетом эллипса. При c = 0 и e = 0 эллипс превращается в окружность.

Второй закон Кеплера (закон площадей)

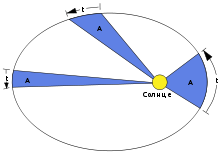
Второй закон Кеплера.

Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.

Применительное к нашей Солнечной системе, с этим законом связаны два понятия: перигелий — ближайшая к Солнцу точка орбиты, и афелий — наиболее удалённая точка орбиты. Таким образом, из второго закона Кеплера следует, что планета движется вокруг Солнца неравномерно, имея в перигелии большую линейную скорость, чем в афелии.

Каждый год в начале января Земля, проходя через перигелий, движется быстрее, поэтому видимое перемещение Солнца по эклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленнее, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу.

Третий закон Кеплера (гармонический закон)

Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей орбит планет. Справедливо не только для планет, но и для их спутников.

, где T₁ и T₂ — периоды обращения двух планет вокруг Солнца, а a₁ и a₂ — длины больших полуосей их орбит.

Ньютон установил, что гравитационное притяжение планеты определенной массы зависит только от расстояния до неё, а не от других свойств, таких, как состав или температура. Он показал также, что третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты:  , где M — масса Солнца, а m₁ и m₂ — массы планет.

Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их орбиты и орбитальные периоды.

Сила тяжести и вес тела. Невесомость Любое тело, находящееся вблизи поверхности Земли, подвергается действию силы тяготения F, под действием которой и в согласии со вторым законом Ньютона тело начнет движение с ускорением свободного падения g. Значит, в системе отсчета, связанной с Землей, на всякое тело массой m действует сила   называемая силой тяжести.  Согласно фундаментальному физическому закону - обобщенному закону Галилея, все тела в одном и том же поле тяготения падают с одинаковым ускорением. Значит, в данном месте Земли ускорение свободного падения равно для всех тел. Оно меняет свою величину вблизи поверхности Земли с широтой в пределах от 9,780 м/с2 на экваторе до 9,832 м/с2 на полюсах. Это обусловлено ,с одной стороны, суточным вращением Земли вокруг своей оси и сплюснутостью Земли - с другой (полярный и экваториальный радиусы Земли равны соответственно 6357 и 6378 км). Так как значения g отличаются незначительно, то ускорение свободного падения, которое мы используем при решении практических задач, принимается равным 9,81 м/с2.  Если пренебречь суточным вращением Земли вокруг своей оси, то сила тяжести и сила гравитационного тяготения равны между собой:    где М - масса Земли; R - расстояние между телом и центром Земли. Эта формула дана для случая, когда тело находится на поверхности Земли.  Пусть тело расположено на высоте h от поверхности Земли, R0 - радиус Земли, тогда    т. е. сила тяжести с удалением от поверхности Земли уменьшается.  В физике существует также понятие веса тела. Весом тела называют силу, с которой тело вследствие тяготения к Земле действует на опору (или подвес), не дающему телу свободно падать. Вес тела проявляется только в том случае, если тело движется с ускорением, отличным от g, т. е. в случае, если на тело кроме силы тяжести действуют другие силы. Состояние тела, при котором тело движется только под действием силы тяжести, называется состоянием невесомости.  Значит, сила тяжести действует всегда, а вес только в случае, когда на тело кроме силы тяжести действуют еще другие силы, вследствие чего тело движется с ускорением а, не равным g g. Если тело перемещается в поле тяготения Земли с ускорением a≠g, то к этому телу приложена дополнительная сила N, причем    Тогда вес тела    т. е. если тело находится в состоянии покоя или движется прямолинейно и равномерно, то а=0 и P'=mg. Если тело движется свободно в поле тяготения по произвольной траектории и в любом направлении, то a=g и Р'=0, т. е. тело будет невесомым. Например, невесомыми являются тела, находящиеся в космических кораблях, которые свободно движутся в космосе.

Первая космическая скорость (круговая скорость) — скорость, которую необходимо придать объекту, который после этого не будет использовать реактивное движение, чтобы вывести его на круговую орбиту (пренебрегая сопротивлением атмосферы и вращением планеты). Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.

Вычисление

В инерциальной системе отсчёта на объект, движущийся по круговой орбите вокруг Земли будет действовать только одна сила — сила тяготения Земли. При этом движение объекта не будет ни равномерным, ни равноускоренным. Происходит это потому, что скорость и ускорение (величины не скалярные, а векторные) в данном случае не удовлетворяют условиям равномерности/равноускоренности движения — то есть движения с постоянной (по величине и направлению) скоростью/ускорением. Действительно — вектор скорости будет постоянно направлен по касательной к поверхности Земли, а вектор ускорения — перпендикулярно ему к центру Земли, при этом по мере движения по орбите эти векторы постоянно будут менять свое направление. Поэтому в инерциальной системе отсчета такое движение часто называют «движение по круговой орбите с постоянной по модулю скоростью»

Часто для удобства вычисления первой космической скорости переходят к рассмотрению этого движения в неинерциальной системе отсчета — относительно Земли. В этом случае объект на орбите будет находиться в состоянии покоя, так как на него будут действовать уже две силы: центробежная сила и сила тяготения. Соответственно, для вычисления первой космической скорости необходимо рассмотреть равенство этих сил.

где m — масса объекта, M — масса планеты, G — гравитационная постоянная (6,67259·10⁻¹¹ м³·кг⁻¹·с⁻²),  — первая космическая скорость, R — радиус планеты. Подставляя численные значения (для Земли M = 5,97·10²⁴ кг, R = 6 371 км), найдем

 7,9 км/с

Первую космическую скорость можно определить через ускорение свободного падения — так как g = GM/R², то

.

Космические скорости могут быть вычислены и для поверхности других космических тел. Например на Луне v₁ = 1,680 км/с, v₂ = 2,375 км/с

Потенциальная энергия.

Потенциальная энергия - энергия взаимодействия тел или частей тела.Потенциальная энергия (от латинского potentia - возможность) определяется взаимным расположением тел или частей  тела, т.е. расстояниями между ними.

Потенциальная энергия тела, поднятого над Землей. Работа силы тяжести

Пусть тело свободно падает с высоты h₁ над уровнем Земли на уровень h₂.

Тогда:

 При падении сила тяжести совершает положительную работу, при движении тела вверх - отрицательную.

Величину  E_з = mgh называют потенциальной энергией взаимодействия тела и Земли.

Т.о.   A = - (E_p2 - E_p1) = -DE_p Работа сила тяжести равна изменению потенциальной энергии, взятому с противоположным знаком. Т.е., если потенциальная энергия увеличивается (тело поднимается), то сила тяжести совершает отрицательную работу и наоборот.

E_з = mgh

 A = - (E_p2 - E_p1) = -DE_p

Т.к. потенциальная энергия определяется координатой, то величина потенциальной энергии определяется выбором системы координат (выбором нулевого уровня). Т.е. она определяется с точностью до постоянной величины.  В данной задаче удобно за точку отсчета выбирать уровень Земли.

Если тело движется под углом к направлению вектора силы тяжести, то, как видно из рисунка, работа силы тяжести  независимо от траектории определяется изменением положения тела (на рис. - высотой наклонной плоскости h).

Если тело движется по произвольной траектории, то ее можно представить в виде суммы горизонтальных участков, на которых работа силы тяжести равна нулю, и вертикальных, на которых суммарная работа будет равна А=mgh.

Работа силы тяжести не зависит от формы траектории и определяется только начальным и конечным положением тела.

На замкнутой траектории работа силы тяжести равна нулю, т.к. потенциальная энергия не меняется.

Потенциальная энергия гравитационного взаимодействия двух материальных точек массами m1 и m2

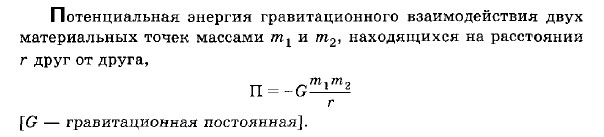
Вторая космическая скорость (параболическая скорость, скорость освобождения, скорость убегания) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала по сравнению с массой небесного тела(например, планеты), для преодоления гравитационного притяжения этого небесного тела. Предполагается, что после приобретения телом этой скорости оно не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).

Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой. Для Земли вторая космическая скорость равна 11,2 км/с. Тело, имеющее около Земли такую скорость, покидает окрестности Земли и становится спутником Солнца. Для Солнца вторая космическая скорость составляет 617,7 км/с.

Параболической вторая космическая скорость называется потому, что тела, имеющие при старте скорость, в точности равную второй космической, движутся по дуге параболы относительно небесного тела. Однако, если энергии телу придано чуть больше, его траектория перестает быть параболой и становится гиперболой; если чуть меньше, то она превращается в эллипс. В общем случае все они являются коническими сечениями.

Вычисление

Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё избесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния.

Запишем закон сохранения энергии

где слева стоят кинетическая и потенциальная энергии на поверхности планеты (потенциальная энергия отрицательна, так как точка отсчета взята на бесконечности), справа то же, но на бесконечности (покоящееся тело на границе гравитационного влияния — энергия равна нулю). Здесь m — масса пробного тела, M — масса планеты, R — радиус планеты, G —гравитационная постоянная, v₂ — вторая космическая скорость.

Решая это уравнение относительно v₂, получим

Между первой и второй космическими скоростями существует простое соотношение:

Квадрат скорости убегания равен удвоенному ньютоновскому потенциалу в данной точке (например, на поверхности планеты):

Тре́тья косми́ческая ско́рость (гиперболическая) — минимально необходимая скорость находящегося у поверхности Земли тела без двигателя, позволяющая преодолеть притяжениеСолнца и уйти за пределы Солнечной системы в межзвёздное пространство^[1].

Взлетая с поверхности Земли и наилучшим образом используя орбитальное движение планеты, космический аппарат может достичь третьей космической скорости уже при 16,6 км/с относительно Земли, а при старте с Земли в самом неблагоприятном направлении его необходимо разогнать до 72,8 км/с. Здесь для расчёта предполагается, что космический аппарат приобретает эту скорость сразу на поверхности Земли и после этого не получает негравитационного ускорения (двигатели выключены и сопротивление атмосферы отсутствует). При наиболее энергетически выгодном старте скорость объекта должна быть сонаправлена скорости орбитального движения Земли вокруг Солнца.

Траектория такого аппарата будет частью дуги параболы (скорость убывает к нулю асимптотически).

Первым земным космическим аппаратом, достигшим третьей космической скорости, стал американский Пионер-10.

Неинерциальные системы отсчета. Силы инерции

Как известно, законы Ньютона выполняются только в инерциальных системах отсчета. Системы отсчета, которые движутся относительно инерциальной системы с ускорением, называются неинерциальными. В неинерциальных системах законы Ньютона, вообще говоря, уже применять нельзя. Однако законы динамики можно применять и для них, если кроме сил, которые обусловленны воздействием тел друг на друга, ввести в рассмотрение понятие силы особого рода - так называемую силу инерции.  При учете сил инерции второй закон Ньютона будет справедлив для любой системы отсчета: произведение массы тела на ускорение в рассматриваемой системе отсчета равно сумме всех сил, действующих на данное тело (учитывая и силы инерции). При этом силы инерции F_in должны быть такими, чтобы вместе с силами F, обусловленными воздействием тел друг на друга, они сообщали телу ускорение а', каким оно обладает в неинерциальных системах отсчета, т. е.   (1)  Так как F=ma (a - ускорение тела в инерциальной системе отсчета), то    Силы инерции обусловлены ускоренным движением системы отсчета относительно измеряемой системы, поэтому в общем случае следует учитывать следующие случаи возниконовения этих сил: 1) силы инерции при ускоренном поступательном движении системы отсчета; 2) силы инерции, которые действуют на тело, покоящееся во вращающейся системе отсчета; 3) силы инерции, которые действуют на тело, движущееся во вращающейся системе отсчета. 

Неинерциальные системы отсчёта (нисо). Описание движения материальной точки в нисо. Силы инерции: переносная, центробежная и кориолисова.

Неинерциальные системы отсчёта (НИСО). НИСО называется система, движищаяся ускоренно относительно инерциальной. СО связана с телом отсчёта, которое, по определению, принимается за абсолютно твёрдое. Опр 2: в СО, в которых имеются силы тяготения и в к-х не выполняется 1-ый з-н Ньютона, наз. НИСО.

Описание движения мат. точки в НИСО. Чтобы описать движение в некоторой СО, необходимо разъяснить содержание высказывания о том, что такие-то события произошли в таких-то точках в такие-то моменты времени. Для этого надо, чтобы в СО  единое время, но в НИСО единого времени в указаном §7 учебника Матвеева смысле не существует. Понятие длительности процессов, начинающихся в одной точке, а заканчивающихся в другой, теряет смысл, посколку скорость хода часов в различных точках различна. Также трудно определить понятие длинны движущегося тела, если не ясно, что такое одновременность в в различных точках. Эти трудности можно частично обойти, если принять во внимание, что интервал собственного времении не зависит от ускорения. Поэтому анализа пространственно-временных соотношений в некоторой бесконечно малой области НИСО можно восползоваться пространтсвенно-временными соотношениями ИСО, которая движэется с той же скоростью, но без ускорения, как и соответствующая бесконечно малая область НИСО. Такая ИСО наз. сопровождающей. Раасмотрим движения с малыми скоростями, когда все эти трудности не возникают и можно использовать преобразования Галлилея, считая, что пространственно-временные соотношения с НИСО таковы же, как если бы она была ИСО.

Силы инерции: переносная и кориолисова. В НИСО  ускорения, которые не связаны с силами такого же характера, какие известны в ИСО. В НИСО, так же как и в инерциальных, ускорения высываются силами, но наряду с «обычными» силами взаимодействия  ещё и силы особой природы, называеммые силами инерции. 2-ой з-н Ньютона формулируется без изменения, но наряду с силами взаимодействия необходимо учесть силы инерции. Силы инерции берутся такими, чтобы обеспечить в НИСО те условия, которые фактически имеются. 2-ой з-н Ньютона в НИСО: ma’=F+F_ин., где a’ – ускорение в НИСО, F – «обычные силы», F_ин – силы инерции. Переносная сила инерции направлена противоположно переносному ускорению НИСО и равна F_ин= – ma₀. Рассмотрим силы инерции во вращающейся СК:

F_ин=m(a’–a)=m(–a₀–a_K)=m²R–2m[ v’]=F_цб+F_К. F_цб= m²R – центробежная сила инерции. F_К=–2m[ v’] – сила инерции связанная с кориолисовым ускорением называется силой Кориолиса. Она перпендикулярна плоскости, в которой лежат векторы угловой и онтосительной скоростей. Если эти векторы колинеарны, то Кориолисово ускорение рауно 0.

Сила Кориолиса

отклоняющая сила вращения Земли

При движении воздушных масс под действием силы барического градиента, они испытывают видимое для наблюдателя с Земли отклонение от своего истинного пути. Это видимое отклонение вызвано действием так называемой "силы Кориолиса" и является следствием вращения Земли.

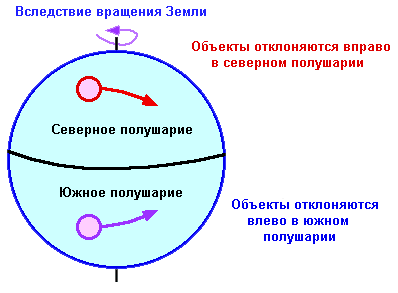
Так как воздушные массы в северном полушарии движутся из области высокого давления в область низкого давления, следовательно они отклоняются силой Кориолиса вправо.

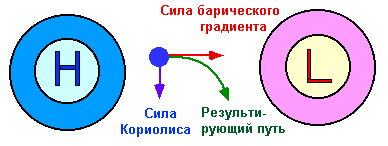
Ниже приведены примеры, иллюстрирующие этот процесс более подробно.

Пример из реальной жизни:  Движение шарика, катящегося по поверхности вращающейся карусели, - это вспомогательная демонстрация силы Кориолиса.

При движении тела относительно вращающейся системы отсчета, кроме центростремительной и центробежной сил, появляется еще одна сила, называемая силой Кориолиса или кориолисовой силой инерции (Г. Кориолис (1792 – 1843) – французский физик).

оявление кориолисовой силы можно обнаружить на следующем примере. Возьмем горизонтально расположенный диск, который может вращаться вокруг вертикальной оси. Прочертим на диске радиальную прямую ОА (рис. 4.10).

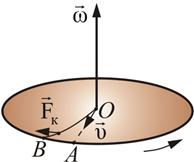  Рис. 4.10

       Запустим в направлении от О к А шарик со скоростью   . Если диск не вращается, шарик должен катиться вдоль ОА. Если же диск привести во вращение в направлении, указанном стрелкой, то шарик будет катиться по кривой ОВ, причем его скорость относительно диска быстро изменяет свое направление. Следовательно, по отношению к вращающейся системе отсчета шарик ведет себя так, как если бы на него действовала сила   , перпендикулярная направлению движения шарика.

       Сила Кориолиса не является «настоящей» в смысле механики Ньютона. При рассмотрении движений относительно инерциальной системы отсчета такая сила вообще не существует. Она вводится искусственно при рассмотрении движений в системах отсчета, вращающихся относительно инерциальных, чтобы придать уравнениям движения в таких системах формально такой же вид, что и в инерциальных системах отсчета.

Чтобы заставить шарик катиться вдоль ОА, нужно сделать направляющую, выполненную в виде ребра. При качении шарика направляющее ребро действует на него с некоторой силой. Относительно вращающейся системы (диска), шарик движется с постоянной по направлению скоростью. Это можно объяснить тем, что эта сила уравновешивается приложенной к шарику силой инерции:

(4.5.5)

Здесь    – сила Кориолиса, также являющаяся силой инерции,    – угловая скорость вращения диска.

       Сила Кориолиса вызывает кориолисово ускорение. Выражение для этого ускорения имеет вид

(4.5.6)

       Ускорение направлено перпендикулярно векторам     и     и максимально, если относительная скорость точки     ортогональна угловой скорости     вращения подвижной системы отсчета. Кориолисово ускорение равно нулю, если угол между векторами     и     равен нулю или  π, либо если хотя бы один из этих векторов равен нулю.

       Следовательно, в общем случае, при использовании уравнений Ньютона во вращающейся системе отсчета, возникает необходимость учитывать центробежную, центростремительную силы инерции, а также кориолисову силу.

       Таким образом,     всегда лежит в плоскости, перпендикулярной к оси вращения. Сила Кориолиса возникает только в случае, когда тело изменяет свое положение по отношению к вращающейся системе отсчета.

       Влияние кориолисовых сил необходимо учитывать в ряде случаев при истолковании явлений, связанных с движением тел относительно земной поверхности. Например, при свободном падении тел на них действует кориолисова сила, обусловливающая отклонение к востоку от линии отвеса. Эта сила максимальна на экваторе и обращается в нуль на полюсах. Летящий снаряд также испытывает отклонения, обусловленные кориолисовыми силами инерции. Например, при выстреле из орудия, направленного на север, снаряд будет отклоняться к востоку в северном полушарии и к западу – в южном. При стрельбе вдоль экватора силы Кориолиса будут прижимать снаряд к Земле, если выстрел произведен в восточном направлении.

       Сила Кориолиса действует на тело, движущееся вдоль меридиана в северном полушарии вправо и в южном – влево (рис. 4.11).

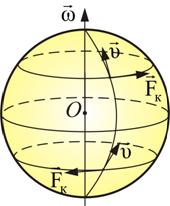
       Это приводит к тому, что у рек подмывается всегда правый берег в северном полушарии и левый – в южном. Эти же причины объясняют неодинаковый износ рельсов железнодорожных путей.

       Силы Кориолиса проявляются и при качаниях маятника (маятник Фуко). Для простоты предположим, что маятник расположен на полюсе (рис. 4.12). На северном полюсе сила Кориолиса будет направлена вправо по ходу маятника. В итоге траектория движения маятника будет иметь вид розетки.

       Как следует из рисунка, плоскость качаний маятника поворачивается относительно Земли в направлении часовой стрелки, причем за сутки она совершает один оборот. Относительно гелиоцентрической системы отсчета дело обстоит так: плоскость качаний остается неизменной, а Земля поворачивается относительно нее, делая за сутки один оборот.

       Таким образом, вращение плоскости качаний маятника Фуко дает непосредственное доказательство вращения Земли вокруг своей оси.

       Если тело удаляется от оси вращения, то сила     направлена противоположно вращению и замедляет его.         Если тело приближается к оси вращения, то     направлена в сторону вращения.

       С учетом всех сил инерции, уравнение Ньютона для неинерциальной системы отсчета (4.5.6) примет вид:

(4.5.7)

 – сила инерции, обусловленная поступательным движением неинерциальной системы отсчета;   – две силы инерции, обусловленные вращательным движением системы отсчета;   – ускорение тела относительно неинерциальной системы отсчета:

   

Состояние идеального газа. Уравнение состояния идеального газа.

   Состояние идеального газа. Частицы (атомы, молекулы) реально существующих газов обладают собственными размерами, занимают некоторый объем пространства, и в некоторой степени зависимы друг от друга. Силы физического взаимодействия между частицами газа затрудняют их движение и уменьшают их подвижность. По этим причинам газовые законы и следствия из них достаточно строго соблюдаются только для разреженных реальных газов, для которых рассояние между частицами значительно превышает собственный размер частиц газа, а взаимодействие между частицами сведено к минимуму. При обычном (атмосферном) давлении газовые законы становятся приблеженными, а при высоком давлении не выполняются совсем.    В связи с этим в науке присутствует понятие о состоянии идеального газа, при котором частицы рассматриваются как геометрические точки с нулевыми размерами и не взаимодействующие друг с другом. Таким образом, идеальный газ - это абстракция, а реальный газ приближается к модели идеального газа тем в большей степени, чем больше различаются температура равновесной конденсации этого газа и температура, при которой этот газ находится.    При комнатной температуре и атмосферном давлении к идеальному состоянию приближаются такие газы, как H₂, N₂, O₂, температуры равновесной конденсации которых равны (округленно) 20K, 77K, 90K. Аммиак и диоксид серы (температура конденсации 240K 263K) далеки от состояния идеального газа, но при 500°C и выше поведение этих газов уже подчиняется, приближенно, уравнению состояния идеального газа.

   Уравнение состояния идеального газа. Значение молярного объема газа, равное 22,4 л/моль, относится к норамльным физическим условиям, под которыми понимаются давление равное 1,01325·10⁵ Па, или 1 атм, и термодинамическая температура, равная 273,15 К (0°C).    Между значениями термодинамической температуры T, выраженной в кельвинах K (не правильно использовать гибридное обозначение кельвина как °K, это запрещено в Международной системе единиц), и температуры Цельсия, выраженной в градусах Цельсия (обозначение °C) существует простая зависимость:

T(K)

=

t(°C) + 273.15

В практических расчетах разность (T - t) можно считать равной 273.    В химических реакциях указанные выше нормальные условия практически не реализуются. Поэтому, прежде чем проводить какие либо расчеты или сопоставления, измеренные при некоторых других условиях объемы газов необходимо пересчитывать применительно к нормальным условиям.

   Для приведения объема газа к нормальным условиям можно пользоваться уравнением объединенного газоваго закона, выведенным французским физиком Клапейроном и носящим его имя:

pV	=	const	или	pV	=	p0V0
-----				-----		-----
T				T		T0

где p (кПа), V (см³, дм³, м³), T (K) - параметры некоторого состояния идеального газа (отличные от н.у.); p₀, V₀, T₀ - параметры, отвечающие нормальным условиям.

   Из последнего уравнения можно рассчитать значение V₀ (объем газа при н.у.), если измерен объем V газа при некоторых других условиях:

V0	=	pVT0
		-------
		p0T

Также легко пересчитать значение V₀ на условия эксперимента:

V	=	p0V0T
		-------
		pT0

   Соотношение pV/T является постоянной величиной при любых заданных значениях p и V для любого измеренного объема идеального газа, следовательно, оно постоянно и для молярного объема идеального газа и при нормальных условиях:

R	=	p0VM	=	101.325 (кПа) · 22,41383 (л/моль)	=	8,31441		кПа · л
		-------		----------------------------------------				---------
		T0		100 (кПа) · 273 (K)				моль · K

Поскольку произведение объема на давление есть энергия W = pV, то и произведение единиц объема (м³) и давления (Па) есть единица энергии - джоуль в СИ (Дж). Следовательно, значение постоянной R в системе СИ составит:

R

=

8.31441 Дж/(моль·K)

Таким образом, для 1 моль идеального газа и, следовательно, всех реальных газов, по свойствам приближающихся к идеальной модели, при нормальных условиях значение R называется универсальной газовой постоянной.

   Соотношение между параметрами идеального газа (давлением p, объемом V, количеством вещества n, термодинамической температурой T) описывает уравнение Клапейрона-Менделеева:

pV

=

nRT

   Уравнение Клапейрона-Менделеева устанавливает связь между давлением, объемом и температурой любой порции газа со свойствами идеальной модели, поэтому называется уравнение состояния идеального газа.    Уравнение состояния идеального газа, позволяет проводить расчеты параметров реальных газов при физических условиях, приближающихся к нормальным условиям.

Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Клапейрона — Менделеева) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

где

 — давление,

 — молярный объём,

 — универсальная газовая постоянная

 — абсолютная температура,К.

Так как  , где   — количество вещества, а  , где   — масса,   — молярная масса, уравнение состояния можно записать:

Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.

В случае постоянной массы газа уравнение можно записать в виде:

Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:

 — закон Бойля — Мариотта.

 — Закон Гей-Люссака.

 — закон Шарля (второй закон Гей-Люссака, 1808 г.)

С точки зрения химика этот закон может звучать несколько иначе: Объёмы вступающих в реакцию газов при одинаковых условиях (температуре, давлении) относятся друг к другу и к объёмам образующихся газообразных соединений как простые целые числа. Например, 1 объём водорода соединяется с 1 объёмом хлора, при этом образуются 2 объёма хлороводорода: