1. Таблицы истинности диаграммы Эйлера – Венна.

Таблица истинности	Диаграмма Эйлера - Венна
А ¬А 0 1 1 0	I Н А Е А А

Рисунок 1 – Свойства логической операции.

Таблица истинности	Диаграмма Эйлера - Венна
А В А∆В 1 1 1 1 0 0 0 1 0 0 0 0	А В

Рисунок 2 –Свойство логической операции «Конъюнкция».

Таблица истинности	Диаграмма Эйлера – Венна
А В А+В 1 1 1 1 0 1 0 1 1 0 0 0	А В

Рисунок 3 – Свойство логической операции «Дизъюнкция».

2. Перевод чисел из одной системы счисления в другую.

Даны три числа системы исчисления:

А=23₁₀ →Ч₂;

В=23₈→Ч_2;

С=1А₁₆→Ч_2;

Д=1111₂→Ч₈;

Е=8Д₁₆→Ч₂;

Решение.

Пуск→Стандартные→Калькулятор→Вид→Программист;

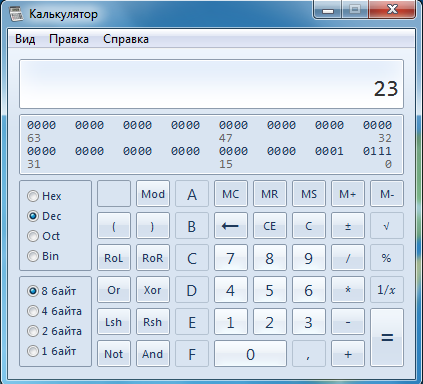(Шаг 1),

(Шаг 2);

Ответы.

А) 10111; С) 11010; Е) 10001101;

В) 10011; Д) 17;

3. Правила перевода чисел из одной системы исчисления в другую.

3.1. Для перевода двоичного числа в десятичное, необходимо записать его в виде многочлена, состоящего из произведений цифр, числа и соответствующей степени числа 2 и вычислить по правилам десятичной арифметики.

(Х₂ = An2^n-1+A_n-12^n-2+…+A₂2¹+A₁2⁰);

Пример 1. Число 11101000₂ перевести Ч₁₀

Решение:

11101000₂ = 1*2⁷+1*2⁶+1*2⁵+0*2⁴+1*2³+0*2²+0*2¹+0*2⁰=232₁₀

3.2. Для перевода восьмеричного в десятичное необходима его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа восемь и вычислить по правилам десятичной арифметики.

(Х₈ = An8^n-1+A_n-18^n-2+…+A₂8¹+A₁8⁰);

Пример 2. Число 75013₈ перевести Ч₁₀

Решение:

75013₈ = 7*8⁴+5*8³+0*8²+1*8¹+3*8⁰ = 31243₁₀

3.3. Для перевода шестнадцатеричного в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16 и вычислить по правилам десятичной арифметики.

(Х₁₆ = An16^n-1+A_n-116^n-2+…+A₂16¹+A₁16⁰);

Пример 3. FDA1₁₆

Решение:

FDA1₁₆ = 1513101₁₆ = 15*16³+13*16²+10*16¹+1*16⁰ = 64929₁₀

3.4. Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор пока не останется остаток меньший или равный 1, число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.

Пример 4. 22₁₀ = (обратном порядке с низу вверх) 0110₂

Решение:

22/2 = 11 (0)

11/2 = 5 (1)

5/2 = 2 (1)

2/2 = 1 (0)

3.5. Для перевода десятеричного числа в восьмеричного его необходимо последовательно делить на 8 до тех пор, пока не останется остаток меньший или равный 7, число в восьмеричной системе записывается как последовательность цифр последовательного результата деления и остатков от деления в обратном порядке.

Пример 5. 571₁₀ = 1073₈

Решение: 571/8 = 71 и т.д.

1 Вариант.

1. 1001011₂→Ч₈ = 113₈;

2. 531₈→Ч₂ = 101011001_2;

3. 6635₈ →Ч₁₆ = D9D;

4. Перевод из системы основания q в систему счисления с основание p.

Задача перевода произвольного числа X заданного в системе с основанием Q в систему с основание P сводится к вычислению полинома вида.

(X = b_nQⁿ+b_n-1Q^n-1+…+b₁Q¹+b₀Q⁰+b_-1Q^-1+…+b_-mQ^-m)

Пример1.

Пусть X = 3⁷7¹1⁰₈

Переведём в десятичную систему счисления:

X = 3*8²+7*8¹+1*8⁰ = 249₁₀

Пример2.

Пусть X = AF,4₁₆

Перевести в десятичную систему счисления:

X = 10*16¹+15*16⁰+4*16^-1 = 175,25₁₀

4. Перевод из системы с основание p в систему с основанием q.

   1. Перевод целых чисел.

Пусть целое число N заданно в системе счисления с основанием P и требуется его перевести в систему с основанием Q.

(N = b_s*Q^s+b_s-1*Q^s-1+…+b₀*Q⁰)

Пример1. N = 47₁₀ = 101111₂

Перевести в десятичную систему счисления

Решение: При делении выделяем целую часть результата и остаток. Остаток записываем в скобках рядом с целой частью. Применим рекуррентную формулу при Q = 2.

47/2 = 23(1)

23/2 = 11 (1)

11/2 = 5 (1)

5/2 = 2 (1)

2/2 = 1 (0)

½ = 0 (1)

Пример 2.

N = 3060₁₀→Q₁₆→BF4₁₆

Решение:

3060/16 = 191(1)

191/16 = 11 (15)

11/16 = 0 (11)

2. Перевод дробных чисел.

Пусть X правильная дробь, которую нужно перевести в Ч_Q систему счисления. Так как X меньше 1, то X_Q системе счисления можно представить в виде формулы:

(N = b_-1*Q^-1=b_-2*Q^-2+…+b_-mQ^-m+…)

Пример 1. X = (0,2)₁₀→Ч₂→0,(0011)₂;

Решение:

0,2*2 = 0,4 = 0 + 0,4 = b_-1 = 0

0,4*2 = 0,8 = 0+0,8 = b_-2 = 0

0,8*2 = 1,6 = 1+0,6 = b_-3 = 1

0,6*2 = 1,2 = 1+0,2 = b_-4 = 1

1. Дано: X = 75₁₀→Ч₂ = 1001011₂

Решение:

75/2 = 37(1)

37/2 = 6(1)

36/2 = 18(1)

18/2 = 9(0)

9/2 = 4(1)

4/2 = 2(0)

2/2 = 1(0)

½ = 0 (1)

2. Дано: X = 0.345₁₀→Ч₂ = 0.(0101)₂

Решение:

0.345*2 = 0.69 = 0+0.69 = b_-1 = 0

0.69*2 = 1.38 = 1+0.38 = b_-2 = 1

0.38*2 = 0.76 = 0+0.76 = b_-3 = 0

0.76*2 = 1.52 = 1+0.52 = b_-4 = 1

0.52*2 =

3) Дано: X = 753.3284₁₀→Ч₂ =

Решение:

753.3284*2 =

Для перевода шестьнадцатиричного числа в двоичное необходимо заменить эквивалентное ей двоичной тетрадой.

13₁₆ →Ч₂ = 11001₂

1₁₆ → 0001₂

3₁₆ → 0011₂

13₁₆ →0001 0011 = 10011₂;

____

15₁₆ → Ч₂ = 10101₂;

1₁₆ → 0001₂

5₁₆ → 0101₂

15₁₆ → 0001 0101 = 10101₂;

Что бы перевести число из двоичной системы в восьмеричную его нужно разбить на триады (тройки цифр) начиная с младшего разряда, в случае необходимости дополняя старшую триаду нулями, а каждую триаду заменяем соответствующей восьмеричной цифрой.

При переходе их восьмеричной системы счисления в шестьнадцатиричную и обратно, необходим промежуточный перевод чисел в двоичную систему.

FEA₁₆ → Ч₈ (сначала перевести в двоичную потом в восьмеричную)

FEA₁₆ → 111111101010₂ далее

111111101010₂ → 7752₈;

n	0	1	2	3	4	5	6	7
8n	1	8	64	512	4096	32768	262144	2097152

Дано:

246₈→Ч₁₆ =

246₈ → А6₂

А6₂ →