Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Рассмотрим линейное неоднородное уравнение второго порядка у''+py'+qy=f(x), где p и q – вещественные числа ; f(x) – непрерывная функция. Как известно, общее решение такого уравнения представляет собой сумму частного решения неоднородного уравнения и общего решения соответствующего однородного уравнения. у_{общ.неодн.}=у_{частн.неодн.}+у_{общ.одн.} Общее решение однородного уравнения мы находить умеем, поэтому остается рассмотреть вопрос о нахождении частного решения. Для нахождения частного решения можно применять метод вариации произвольных постоянных. Однако , если в правой части уравнения (1) – многочлен, либо показательная функция, либо тригонометрическая функция, либо тригонометрическая функция, либо тригонометрическая функция sin , либо линейная комбинация перечисленных функций, то частное решение может быть найдено методом неопределенных коэффициентов, не содержащим процессы интегрирования. Рассмотрим различные виды правых частей (1). 1) Правая часть имеет вид: f(x)=P_n(x), где P_n(x)=a₀xⁿ+a₁x^n-1+…+a_n-1x+a_n. многочлен степени n. Тогда частное решение у можно искать в виде у=Q_n(x)xⁿ, где Q_n(x) – многочлен той же степени, что и P_n(x), а Р – число корней характеристического уравнения, равных нулю. Пример 1: Найти общее решение уравнения у''-2у'+у=х+1. Решение: Общее решение соответствующего однородного уравнения имеет вид Y=(C₁+C₂x)e^x. Так как правая часть уравнения - многочлен первой степени и ни один из корней характеристического уравнения К²-2К+1=0 не равен нулю (к₂=к₁+1), то частное решение ищем в виде у=(А_х+В)_х=А_х+В, где А и В – неизвестные коэффициенты. Дифференцируя дважды у=А_х+В и подставляя у, у' и у'' в данное уравнение, найдем -2А+А_х+В=х+1. Приравнивая коэффициенты при одинаковых степенях х в обеих частях равенства: А=1, -2А+В=1, находим А=1, В=3. Итак, частное решение данного уравнения имеет вид у=х+3, а его общее решение у=(С₁+С_2х)е^х+(х+3). 2) Правая часть имеет вид f(x)=e^{альфа х} * Рn(х), где Рn(х) – многочлен степени n. Тогда частное решение у(с загагуленой сверху хД) следует искать в виде у=Q_n(x)x^re^{альфа х}, где Q_n(x) – многочлен. Ещё чуть-чуть нужно переписать!! (не успел) .

28.11.11.

f(x)=e^dx*Pn(x) y (значок над ним)=Q_n(x)x^re^dx Пример: найти общее решение ур-ния. уⁿ-4y'+3y=xe^x. Решение: Характеристическое ур-ние k²-4k+3=0. имеет корни k₁=1, k₂=3. Значит, общее решение соответствующего однородного ур-ния имеет вид Y=C₁e^x+C₂e^3x. В правой части этого ур-ния – произведение многочлена первой степени на показательную функцию e^dx при =1. Т.к. среди корней характеристического ур-ния имеется только один корень k₁= , то r=1. В данном случае P_n(x)=x – многочлен первой степени. Поэтому частное решение данного уравнения ищем в виде y(с этой хренью)=(Ах+В)хе^х=(Ах²+Вх)е^х. Дифференцируя и подставляя в ур-ие, получаем -4А+2А-2В=х. Приравнивая кэффициенты при одинаковых степенях х в обеих частях равенства -4А=1, 2А-2В=0, находим: А=-1/4, В=-1/4. Подставляя найденные значения А и В в выражение для у(с хренью), получаем частное решение дано уравнения у(с хренью)=-(1/4)(х²+х)е^х, общее решение имеет вид у=у(с хренью сверху)+Y=С₁е^х+С₂е^3х-1/4(х²+х)е^х 3) Правая часть имеет вид f(x)=аcos x+bsin x, где а, бета, в – известные числа. Тогда частное решение у(с хр) надо искать в виде у(с хр)=(Аcosx*бетах+Bsinбетах)х^r, где А и В – неизвестные коэффициенты, r – число корней характеристического, равных i*бета. Пример 6: Найти общее решение ур-ия уⁿ+у=sinx. Решение: Характерис-ое ур-ие k²+1=0 имеет корни k₁=i, k=-i. Поэтому общее решение соответствующего однородного ур-ия у=С₁cosx+C₂sinx. В правой части равенства – тригонометрическая функция sinx, т.е. а=0, в=1, бета=1. Т.к. i*бета=i – корень характерист-го ур-ия, то r=1 и частное решение надо искать в виде: у(с хр)=(Acosx+Bsinx)x. Дифференцируя и подставляя в ур-ие, получаем 2(-Аsinx+Bcosx)=sinx, откуда А=-1/2, В=0. Таким образом, частное решение у(с хр)=-1/2xcosx, общее решение у=у(с хр)+Y=C₁cosx+C₂sinx-1/2xcosx. Пример. Найти общее решение ур-ия у''+у=sin2x. Решение: Данное ур-ие отличается от предыдущего только тем, что бета=2. Т.к. i*бета=i2 не является корнем характерист.ур-ия, то r=0 и частное решение следует искать в виде: у(с хр)=Аcos2x+Bsin2x. Дифференцируя и подставляя в ур-ие, получаем -3Аcos2x-3Bsin2x=sin2x, откуда А=0, В=-1/3, т.е. частное решение у(с хр)=-1/3sin2x, общее решение ур-ия у=у(с хр)+Y=С₁cosx+C₂sinx-1/3sin2x. 4) Правая часть имеет вид f(x)e^ax[Pn(x)cos*бета*x+Pm(x)sin*бета*х], где Pn(x) - многочлен степени n, а Pm(х) – многочлен степени m. Тогда частное решение следует искать в виде у(с хр)=х^re^ax[Q₁(x)cos*бета*х+Q₂x)sin*бета*х], где Q₁(x) and Q₂(x) - многочлены степени S, S=max{n,m}, а r – число корней характерист-го ур-ия, равных альфа+i*бета. Пример: Найти общее решение ур-ия у''-e=3e^2xcosx. Решение: Здесь характреист-ое ур-ие k²-1=0 имеет корни k₁=1, k₂=-1. Общее решение однородного ур-ия таково: Y=C₁e^x+C₂e^-x. В правой части ур-ия произведение многочлена нулевой степени, показательной и тригонометрической функций, так что Pn(x)=3, Pm(x)=0, S=0. Число альфа+i*бета=2+i1 не является корнем характерист-го ур-ия, поэтому r=0, и частное решение ищем в виде у(с хр)=e^2x(Acosx+Bsinx). Дифференцируя и подставляя в ур-ие, получаем (2А+4В)cosx+(2B-4A) sin=3cosx. Приравнивая коэффициенты при cosx and sinx, находим 2А+4В=3, -4А+2В=0, откуда А=3/10, В=3/5. Таким образом, частное решение у(с хр)=е^2х(3/10*cosx+3/5sinx). Общее решение: e^2x(3/10*cosx+3/5sinx)+C₁e^x+C₂e^-x.

Задача Коши и краевая задача для ур-ний 2-го порядка.

05.12.

Для однозначного опр. Решения дифференциального ур-ния 2-го порядка необходимо задать два случая, чтобы найти неопределенные коэффициенты и .

Здесь возможно 2 случая:

1. Задача Коши, когда согласно теореме, в одной точке 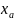задаются значения искомой ф-ции и её производной – 2 начальных условия.

2. Краевая задача, когда в конечных точках интервала решения, задается по одному условию, например, .

Пример:

Найти решение ур-ния:

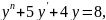
Удовл. краевым условиям

Решение: характеристическое ур-ние данного дифференциального ур-ния имеет вид:

Его корни вещественны и различны:

Следовательно, общее решение однородного ур-ния имеет вид:

Исходя из вида правой части, будем искать частное решение данного неоднородного ур-ния в виде константы . Подставляя его решение в ур-ние, получаем . Отсюда следует, что общее решение неоднородного ур-ния имеет вид:

Для отыскания частного решения, соответствующего данным краевым условиям, подставим это решение в краевые условия. Получим систему линейных ур-ний относительно произвольных постоянных и

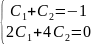
Из этой системы находим:

Отсюда решение данной краевой задачи как частное решение дифференциального ур-ния, проходящая через точки и , имеет вид:

12.12.11. Пусть у=у(t) – объем производства. Тогда функция у=у(t) удовлетворяет ур-ие y=ky. Ур-ие является ур-ем с разделяющимися переменными. Его решение имеет вид y=y₀e^k(t—t0) Ур-ие описывает также рост народонаселения, динамику роста цен при постоянной инфляции и т.д. Выяснить, по истечении какого промежутка времени объем реализованной продукции удвоится по сравнению с первоначальным, если значение коэффициента пропорциональности k в уравнении равно 0,1. На сколько % следует увеличить норму инвестиций, чтобы промежуток времени, необходимого для удвоения объема реализованной продукции уменьшился на 20%. Решение: t₀=0, k=0,1, y-2y₀ следовательно, 2y₀=y₀e^0,1t(2) t=10 ln2»приближенно равно»6,93 t₁=0,8t следовательно, k₁=k/0,8=1,25k, следовательно, норму инвестиций следует увеличить на 25%. Предположение о неизменности цен на практике оказывается справедливости лишь для узких временных интервалов. р – убывающая функция от объема у реализованной продукции (р=р(у) ), следовательно, у'= mlp(y)y(3) Уравнение вида (3) описывает также рост народонаселения при наличии ограничений для этого роста, динамику развития эпидемии, процесс распространения . . . (дальше не успел написать определение и ещё пример) Интегрирование дифференциальных уравнений с помощью рядов. В тех случаях, когда для уравнения y'=f(x,y) требуется решить задачу Каши при начальном условии у│_х=х0=у₀│ решение можно искать с помощью ряда Тейлора: ПР-Р: у=∑ (бесконечность сверху и n=0 снизу) y⁽ⁿ⁾(x₀)/n! * (x-x₀)ⁿ, где у(х₀)=у₀, у'(х₀)=f(x₀,y₀), а дальнейшее произведение y⁽ⁿ⁾(x₀) находят последовательности дифференцированием исходного ур-ия и подстановкой в результат дифференцирования вместо х, у, у' . . . значений х₀, у₀, у₀ и всех остальных найденных последующих производных. Пример1: Проинтегрировать приближенно с помощью рядя Тейлора уравнения у=х²+у², у(0)=1, взяв, шесть первых членов разложения, отличных от нуля. Из уравнения начальных условий, находим у'(0)=0²+1²=1. Дифференцируя данное урав-ие, последовательных получаем: у''=2х+2уу', у'''=2+2у^'2+2уу'', у''''=6у'у^'''', у^'''''=6у^''2+8у'у+2уу^'''', Полагая х=0 и используя значения у(0)=1, у^'(0)=1, последовательно находим у^''(0)=2, у'''(0)=8, у''''(0)=28, у''''^'(0)=144. Искомое решение имеет вид: у=1+х/1!+2х²/2!+8х³/3!+28х⁴/4!+144х⁵/5! + . . . Пример 2 (писать не стал)