Теорема Абеля.

26.09

1. Если степенной ряд сходится при некотором значении , то он сходится абсолютно при всех значениях х, таких, что .

2. Если степенной ряд расходится при , то он расходится при всех значениях х, таких, что

Из т. Абеля следует, что существует такое число , что, при ряд сходится, а при , ряд расходится. Вопрос о сходимости ряда, при требует дополнительных исследований.

Радиусом сходимости степени ряда называется такое число что ряд сходится при находится по следующей формуле

Пример:

Рассмотрим ряд

Следовательно данный ряд сходится на интервале Исследуем поведение ряда на концах интервала сходимости, т.е. в точке при получим гармонический ряд

И при x=1, ряд , ряд ряд , который сходится в силу признака Лейбница.

Таким образом, данный ряд сходится в любой точке полуинтервала и расходится вне его.

Пример:

Ряд

расходится по всей числовой прямой, кроме точки , т.к. его радиус сходимости:

Дифференциальные уравнения.

10.10

Основные понятия.

Дифференциальным уравнением называется уравнение вида (1), где х-независимая переменная, искомая ф-ция, - её произведение. Решением дифференциального ур-ния называется такая ф-ция , которая при подстановке её и её производных обращает равенство (1) в тождество.

Порядком дифференциального ур-ния называется наибольший порядок n входящий в него производной.

Примеры:

1. Решить дифференциальное ур-ние:

Запишем ур-ние в виде

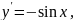
По определению первообразной, решение этого ур-ния является первообразная для ф-ция . Поэтому решение данного ур-ния имеет вид:

Интегральной кривой называется график решения дифференциального ур-ния. Например, для ур-ния интегральные кривые являются графиками ф-ции , полученный из графика сдвигом вверх (или вниз) на константу .

Общим решением дифференциального ур-ния.

Порядка n называется такое решение , которое является ф-ций от независимой переменной х и от n производных независимых постоянных .

Частным решением называется решение, получаемое из общего решение при некоторых конкретных значениях постоянных .

Пример: Для ур-ния второго порядка общее решение имеет вид . Одним из частных решений будет решение , полученное при ,

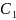Дифференциальные ур-ния первого порядка.

Разрешенным относительно производной называется дифференциальное ур-ние первого порядка

Которое можно записать в виде

Решение разделяющимися переменными.

Решение ур-ний вида (2) сводится к нахождению неопределенных интегралов, если ф-ция двух переменных представима в виде произведения двух ф-ций одной переменной . Заменяя на получаем

Ур-нием с разделяющимися переменными называется (3)

По-другому такие ур-ния можно записать в виде

Или

Интегрируя обе части последнего равенства, получаем

Общее решение заданное в неявном виде, называется общим интегралом этого ур-ния.

Геометрически общее решение (и общий интеграл) представляет собой семейство интегральных кривых на плоскости, зависящее от одного параметра .

Частным решением ур-ния называется решение, полученное из общего решения при фиксированном значении . , где - число аналогично определяется частный интеграл

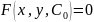
Задача Коши.

Лекция № ? 17.10.11.

Уравнения с разделяющими переменными. Дифференциальные уравнения.

Пример 1: Пусть мы имеем уравнение d² *y/d_x*x² =0 Функция y=sinx, y=2cosx, y=3sinx-cosx и вообще функция вида y=C, sinx, y=C₂cosx или y=C, sinx-C₂cosx являются решениями данного уравнения при любом выборе постоянных С₁ и С₂ , в этом легко убедиться, подставив указанные функции в уравнение. Наряду с обыкновенными дифференциальными уравнениями . . . Пример 2: Рассмотрим уравнение y'x-x²-y=0. Его решениями будут все функции вида y=x²+C_x , где С – любое постоянное. Действительно, дифференцируя функцию y=x²+C_x. Находим: y'=2x+C. Подставляя выражения y и y' в исходное уравнение, получаем тождество (2х+С)х-х²-С_х=0. Каждое из уравнений, рассмотренных в примерах 1 и 2, имеет бесчисленное множество решений.

Пример 3: Рассмотрим уравнение у'=у/х. Функция f(x,y)=y/x не определена при х=0, следовательно, поле направлений для данного у . . . Разделяя переменные, получаем: dy/y=dx/x Интегрируя, имеем ∫dy/y=∫dx/x+ln│C₁│, C₁≠0, или ln│x│+ln│x│+ln│C₁│. Потенцируя (избавляясь от знака логарифма) , находим │у│=│ ││х│, что эквивалентно уравнению у=±С₁х. Полагая ± С₁ =С, окончательно получаем у=С_х – общее решение данного уравнения, где С – произвольная постоянная, которая может принимать как положительные, так и отрицательные значения, но С≠0. Заметим, что у=0 , также решение уравнения (оно было потеряно при делении на у). Это решение может включить в (9), если считать, что постоянная С принимает и значение С=0 . Геометрическими общее решение (9) представляет собой семейство прямых проходящих через начало координат. Пусть требуется выделить из общего решения (9) частное решение удовлетворяющее следующим начальным условиям: Х₀=1, у₀=2. Подставляя эти значения в общее решение (9) вместо х и у , получаем 2=С*1, откуда С=2. Таким образом, искомое частное решение у=2х. Пример 4: Для уравнения первого порядка dy/dx=-y/x общим решением будет семейство функции у=С/х, это можно проверить простой подстановкой в уравнение. Найдем частное решение, удовлетворяющее следующему начальному условию: у₀=1 при х₀=2. Подставляя эти значения х₀ и у₀ в формулу у=С/х, получаем 1=С/2. Следовательно, искомым частным решением будет функция у=2/х. (далее график на листке)

Частное решение у=2х : (далее график на листке) Найдите дифференциальное уравнение семейства парабол у=С_х2 (это х²) Дифференцируя по х уравнение семейства, найдем dy/dx=2cx Подставляя сюда значение С=у/х² из уравнения семейства получаем дифферинцируя данного семейства. dy/dx=2у/x Это дифференцированное уравнение имеет смысл при х≠0, т.е. в любой области, не содержащей точек на оси Оу.