Восстанавливаемые элементы

Количественными показателями безотказности восстанавливаемых элементов (объектов) являются: вероятность безотказной работы, средняя величина наработки на отказ, характеристика и параметр потока отказов.

Таким образом, по сравнению с рассмотренными выше показателями безотказности, появился новый, характерный только для восстанавливаемых элементов термин – поток отказов. Что это за показатель?

В течение времени эксплуатации локомотивов наблюдаются следующие периоды: работа, проведение технического обслуживания, текущих и капитальных ремонтов, возможны отказы и связанные с ними простои локомотивов в неплановых ремонтах, перерывы в работе или простои по организационным причинам.

Наглядное представление о функционировании локомотива во времени даёт временная диаграмма его использования (см. рис.4.4). На этой диаграмме по оси времени от некоторого начального промежутка можно показать периоды работы локомотива (Р), периоды выполнения технического обслуживания (ТО) и текущих ремонтов (ТР), а также периоды времени, связанные с простоями при восстановлении работоспособности после отказов (В), и перерывов в работе (П). Моменты времени отказов обозначены крестиками, а моменты времени окончания восстановления работоспособности – точками. Длительность интервалов времени каждого из отмеченных периодов является случайной величиной.

Аккуратно построенная временная диаграмма, несмотря на свою простоту, содержит обширную информацию о надёжности объекта наблюдения. При коротких интервалах Р объект имеет низкую безотказность. При длинных интервалах В, ТО и ТР – изделие имеет низкую ремонтопригодность и эксплуатационную технологичность. В то же время большая протяжённость интервалов Р может свидетельствовать о достаточно высокой долговечности.

Поскольку моменты времени следования событий, указанных на временной диаграмме, образуют последовательность событий, происходящих одно за другим в некоторые моменты времени, а эти моменты времени случайны, то мы и получаем случайный поток событий.

Рис. 4.4. Временная диаграмма следования событий

Для таких случайных потоков событий безотказность оценивается без учёта пребывания в плановом обслуживании, текущем ремонте и восстановлении локомотивов после отказа, не учитываются также и перерывы в работе. После исключения указанных выше интервалов временная диаграмма модели безотказности содержит только следующие друг за другом интервалы работы до наступления отказов. Таким образом, временная диаграмма должна рассматривается только как поток отказов. Наработка между отказами, являющаяся суммой многих периодов безотказной работы, соответствует ресурсу восстанавливаемого объекта и является величиной случайной.

До момента первого отказа, показатели безотказности могут рассчитываться точно также, как и для невосстанавливаемых элементов. Кроме этого, рассмотренные нами ранее правила и зависимости для расчёта количественных показателей вероятности безотказной работы и средней наработки на отказ для неремонтируемых элементов могут быть использованы и для ремонтируемых (восстанавливаемых), но при использовании законов распределения, учитывающих особенности формирования потока отказов. В самом деле, поток однородных событий (отказов) наглядно изображается последовательностью точек с интервалами между ними

При вероятностном описании поток событий можно представить как последовательность случайных величин и т.д.

Понятие потока событий заимствовано из теории массового обслуживания, имеющей проверенные многолетней практикой методы решения подобных задач. При анализе потока событий выделяют свойства стационарности, отсутствия последействия и ординарности.

Свойство стационарности состоит в том, что вероятность появления событий (отказов) на любом интервале времени зависит только от числа и от длительности интервала и не зависит от начала его отсчёта. Стационарный поток имеет постоянную интенсивность, т.е. среднее число отказов в единицу времени не меняется.

Свойство отсутствия последействия состоит в том, что вероятность появления событий (отказов) на любом интервале времени не зависит от числа событий на предшествующих интервалах времени. Другими словами, предшествующая работа локомотива не оказывает влияния на вероятность появления его отказов в ближайшем будущем. Отсутствие последействия в потоке практически означает, что события (отказы), образующие поток, появляются независимо друг от друга.

Свойство ординарности состоит в том, что вероятность появления более одного события (отказа) на элементарном интервале наработки пробега пренебрежимо мала по сравнению с вероятностью появления только одного события (отказа). Таким образом, появление более одного отказа за малый промежуток пробега практически не возможно. Свойство ординарности практически означает, отказы в потоке появляются поодиночке, а не группами по два, по три и т.д.

Теперь введём понятие – характеристика потока отказов Величина следует из интерпретации ординарного потока событий как случайного процесса, который скачкообразно возрастает на одну единицу в моменты появления отказов, как графически изображено на рис. 4.5,а.

Число отказов за пробег для совокупности локомотивов будет равно

а для одного локомотива, соответственно, составит

По мере увеличения число скачков, изображённых на рис. 3.5,а, становится больше, а сами скачки, по амплитуде, – будут меньше. В пределе, при , мы и получаем характеристику (функцию) потока отказов

к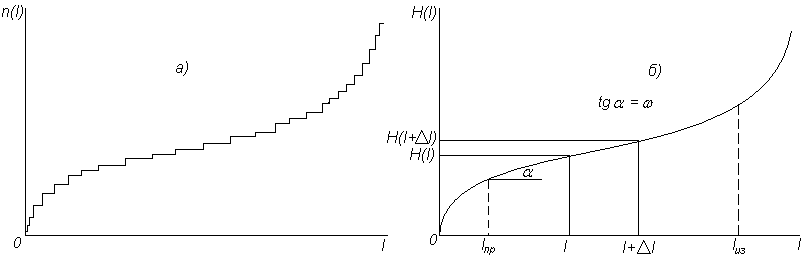 оторая возрастает плавно, а не скачкообразно (см. рис. 3.5.б).

Рис. 4.5. Вид функции (характеристики) потока отказов

В период нормальной эксплуатации функция потока отказов часто оказывается линейной, как показано на рис. 3.5,б. Это следует из свойства стационарности потока после периода приработки деталей

где носит название параметр потока отказов.

Параметр (интенсивность) потока отказов – есть первая производная от функции (характеристики) потока отказов

В статистической трактовке величина оценки параметра потока отказов вычисляется на основе выражения

где - количество наблюдаемых локомотивов (элементов); интервал наработки; число отказов каждого локомотива (элемента) до наработки ; число отказов в пределах наработки

Таким образом, параметр потока отказов – это отношение среднего числа отказов за произвольно малую наработку к значению этой наработки. В железнодорожной практике размерность параметра потока отказов - , или количество отказов, приходящихся на один миллион километров пробега локомотивов.

_{Для нестационарного потока параметр потока отказов зав}исит от величины наработки , а для стационарного потока параметр

Среднее число отказов на интервале наработки (0, ) является функцией потока отказов и выражается через параметр потока отказов интегрированием производной в пределах от 0 до . С учётом того, что величина

При постоянной величине параметра потока отказов

Величина средней наработки между отказами является очень важным параметром как потока отказов локомотива и его элементов конструкции, так и потока восстановления их работоспособности.

Средняя наработка между отказами на интервале будет равна

В пределе при , получаем

Геометрический смысл полученного соотношения состоит в том, величина средней наработки между отказами потока численно равна величине , образованного осью ординат и касательной к функции потока отказов в интересующей нас точке.

В статистической трактовке величина средней наработки на отказ рассчитывается в виде

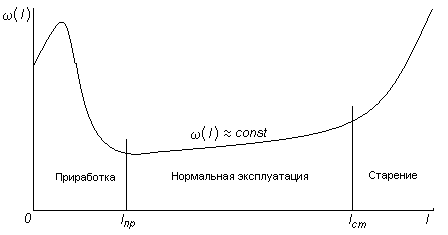Изменение параметра потока отказов за время эксплуатации объектов характеризуется тремя периодами: приработки , нормальной эксплуатации , периода старения или изнашивания , как показано на рис. 4.6.

Рис. 4. 6. Характер изменения параметра потока отказов объекта за время его использования по назначению

В случае ординарного потока без последействия понятия интенсивности отказов для невосстанавливаемых элементов и параметра потока отказов - для восстанавливаемых элементов, совпадают.

Пример. В локомотивном депо ведётся наблюдение за работой 44 дизелей, прошедших капитальный ремонт. При наработке за период от 0 до 220·10³ км были зафиксированы отказы: при наработке ; после наработки ещё 11 отказов; после наработки ещё 8 отказов; после наработки ещё 3 отказа; после наработки

Все отказавшие дизели были восстановлены и участвовали в наблюдении на протяжении 220·10³ км. Считая поток отказов дизелей простейшим, необходимо определить вероятность отказа и вероятность их безотказной работы в разные моменты времени, а также рассчитать характер изменения параметра потока отказов дизелей в функции от наработки.

1. Интервал наработки .

2.Интервал наработки

3. Интервал наработки .

и т.д.

В тоже время, в случае определения интересующих нас показателей за интервал наработки дизелей от 80 до 120·10³ км мы получим