
- •События и их возможные исходы
- •Функции распределения случайных величин
- •Количественные показатели надёжности
- •Восстанавливаемые элементы
- •Показатели долговечности
- •Показатели ремонтопригодности
- •Показатели сохраняемости
- •Комплексные показатели надёжности
- •Математическая модель внезапного отказа
- •Анализ закономерностей, описывающих процессы изнашивания, старения и усталостного повреждения деталей и узлов локомотивов
- •Понятие о параметрической надёжности
- •Требования к информации о надёжности, методы её сбора, анализа и автоматизации
- •Характеристика исходных предпосылок оптимизации межремонтных пробегов
- •Модель оптимизации межремонтного периода исходя из экономической целесообразности
- •Управление надёжностью локомотивного парка депо
- •Технические особенности обеспечения надёжности локомотивного парка
Модель оптимизации межремонтного периода исходя из экономической целесообразности
При разработке системы технического обслуживания и ремонта локомотивов возможны, по крайней мере, два подхода: поэлементный и интегральный. В первом случае определяются межремонтные периоды для каждого элемента, после чего их группируют, получая соответствующий ремонтный цикл для локомотива. Во втором случае локомотив рассматривается как единая нераздельная система.
Критерии оптимальности межремонтных периодов и математические модели в указанных случаях различны и будут рассмотрены ниже.
Для разработки математической модели оптимизации длительности работы элемента конструкции локомотива до планового ремонта можно использовать информацию о его надежности в различном виде. Наибольшее применение находят закон распределения длительности работы до отказа и закономерности накопления износа (старения) элемента во времени.
Если
бы все детали имели одинаковую
детерминированную долговечность,
измеряемую пробегом до отказа
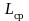 ,
то вопрос выбора срока ремонта (в данном
случае --
замены) решался бы просто. За
межремонтный период
,
то вопрос выбора срока ремонта (в данном
случае --
замены) решался бы просто. За
межремонтный период
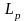 следовало бы принять именно величину
.
При этом за межремонтный период не было
бы отказов, ресурс каждой детали был
бы использован полностью.
следовало бы принять именно величину
.
При этом за межремонтный период не было
бы отказов, ресурс каждой детали был
бы использован полностью.
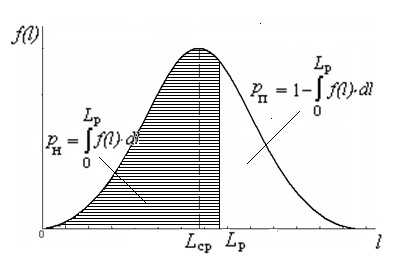
Рис. 7.4. Сотношение вероятностей неплановых и плановых ремонтов в зависимости от величины межремонтного пробега
К
сожалению, на практике однотипные детали
имеют не детерминированную, а случайную
наработку до отказа, имеющую разброс
относительно среднего значения
и описываемую некоторым законом
распределения
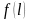 .
Это вносит неопределенность и сложность
в решение задачи выбора межремонтного
периода.
.
Это вносит неопределенность и сложность
в решение задачи выбора межремонтного
периода.
В самом деле, если по-прежнему взять межремонтный период, равный , то за этот срок примерно половина деталей будет иметь отказы со всеми втекающими вредными последствиями, у второй же половины деталей, замененных на плановом ремонте, будет недоиспользован ресурс. В этой ситуации имеются две составляющие затрат: на выполнение неплановых ремонтов с учетом ущерба от отказов локомотива на линии и на выполнение плановых ремонтов.
При
изменении межремонтного периода
в сторону уменьшения или увеличения
относительно
(рис.7.4) будут изменяться указанные
составляющие затрат и их сумма. Целью
математической модели оптимизации
межремонтного периода является
нахождение зависимости суммарных затрат
от межремонтного периода
и нахождение такого его значения
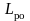 ,
которое соответствует минимальным
суммарным затратам.
,
которое соответствует минимальным
суммарным затратам.
Вероятность
отбраковки детали на плановом ремонте
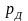 зависит от совершенства методов и
технических средств диагностирования
деталей, допусков на их рабочие параметры,
квалификации ремонтного персонала и,
в общем случае, находится в пределах
зависит от совершенства методов и
технических средств диагностирования
деталей, допусков на их рабочие параметры,
квалификации ремонтного персонала и,
в общем случае, находится в пределах
 .
.
При
невозможности установить на плановом
ремонте техническое состояние детали
из-за отсутствия средств диагностирования
применяется жесткая стратегия замен,
когда все оставшиеся целыми детали
заменяются, т.е.
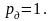
Если
принять, что на плановом ремонте
заменяются все оставшиеся детали, после
неплановой замены отказавших деталей,
то есть
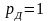 .
В этом случае можно записать следующие
выражения
.
В этом случае можно записать следующие
выражения
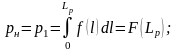
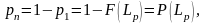
где
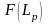 --
вероятность отказа за пробег
--
вероятность отказа за пробег
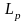 ;
;
 --
вероятность безотказной работы за
пробег
.
--
вероятность безотказной работы за
пробег
.
За
период
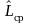 деталь будет заменена на неплановом
ремонте с вероятностью
деталь будет заменена на неплановом
ремонте с вероятностью
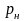 или на плановом ремонте с вероятностью
или на плановом ремонте с вероятностью
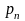 ,
поэтому математическое ожидание
суммарных затрат на этот период
,
поэтому математическое ожидание
суммарных затрат на этот период
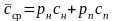 , (7.1)
, (7.1)
а удельные затраты на единицу наработки
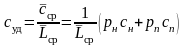 , (7.2)
, (7.2)
где
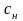 --
средние расходы (с учетом ущерба от
отказов на линии) при замене (ремонте)
на неплановом ремонте детали;
--
средние расходы (с учетом ущерба от
отказов на линии) при замене (ремонте)
на неплановом ремонте детали;
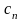 --
то же при плановой замене.
--
то же при плановой замене.
Для удобства дальнейшего анализа и унификации модели рассмотрим относительные суммарные затраты за пробег в долях затрат на неплановом ремонте
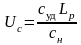 . (7.3)
. (7.3)
После преобразования выражения (7.3) с учетом уравнений (7.1), (7.2) окончательно получим
 , (7.4)
, (7.4)
где
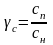 .
.
Поскольку условия работы и интенсивность использования локомотивов на различных участках железных дорог существенно различаются, то и экономические последствия отказов также будут различными. Они должны определяться на основании статистических данных, полученных в конкретных условиях эксплуатации локомотивов.
Средние
затраты при замене (или ремонте) одной
детали
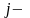 го
типа на плановом виде ремонта, где
разборка и восстановление данной детали
предусмотрены по циклу, определяются
по формуле
го
типа на плановом виде ремонта, где
разборка и восстановление данной детали
предусмотрены по циклу, определяются
по формуле
 , (7.5)
, (7.5)
где
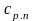 --
стоимость разборки-сборки и дефектировки
детали на плановом ремонте;
--
стоимость разборки-сборки и дефектировки
детали на плановом ремонте;
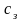 --
стоимость замененной детали (в случае
восстановления детали
=
0);
--
стоимость замененной детали (в случае
восстановления детали
=
0);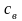 --
стоимость восстановления детали (при
замене детали новой
= 0).
--
стоимость восстановления детали (при
замене детали новой
= 0).
Неплановый ремонт может иметь место в случае отказа детали или узла в период между плановыми ремонтами локомотива (порча с требованием резерва, порча без требования резерва, неплановый ремонт). Но неисправность может быть обнаружена и при проведении планового ремонта, на котором ремонт этой детали или узла не предусматривается циклом. В любом из этих случаев локомотив становится на неплановый ремонт (или имеет перепростой на плановом ремонте из-за сверхцикловых работ). При этом, кроме затрат на замену (ремонт) детали, необходимо учесть ущерб от потери локомотиво-часов (при неплановом ремонте без порчи) от потери пассажирских и грузовых поездо-часов (в случае порчи на линии).
Учитывая это, экономические потери, связанные с проведением непланового ремонта локомотива, определяются по формуле
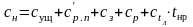 , (7.6)
, (7.6)
где
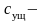 убытки, связанные с простоем поездов
на участке обращения в связи с отказом
(порчей) локомотива, р.;
убытки, связанные с простоем поездов
на участке обращения в связи с отказом
(порчей) локомотива, р.;
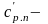 средняя стоимость разборки-сборки
детали (узла) на неплановом ремонте,
р. Как правило, на практике имеет место
соотношение
средняя стоимость разборки-сборки
детали (узла) на неплановом ремонте,
р. Как правило, на практике имеет место
соотношение
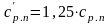 ;
;
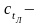 стоимость одного локомотива-часа
простоя, р.;
стоимость одного локомотива-часа
простоя, р.;
 величина среднего простоя локомотива
на неплановом ремонте в результате
отказа (порчи) на линии, ч.
величина среднего простоя локомотива
на неплановом ремонте в результате
отказа (порчи) на линии, ч.
Средневзвешенные убытки, связанные с простоем поездов на участке обращения в связи с отказом (порчей) локомотива рассчитываются в виде
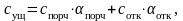 (7.7)
(7.7)
где
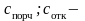 убытки железной дороги, связанные с
порчей и отказом локомотива на линии;
убытки железной дороги, связанные с
порчей и отказом локомотива на линии;
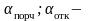 доля порч в общем количестве отказов и
доля неплановых ремонтов без порч.
доля порч в общем количестве отказов и
доля неплановых ремонтов без порч.
Величина
 может быть рассчитана в виде отношения
может быть рассчитана в виде отношения
 ,
,
где
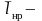 величина средней наработки элемента
(узла) конструкции локомотива на
неплановый ремонт;
величина средней наработки элемента
(узла) конструкции локомотива на
неплановый ремонт;
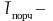 величина средней наработки элемента
(узла) конструкции локомотива на порчу.
величина средней наработки элемента
(узла) конструкции локомотива на порчу.
Доля
неплановых ремонтов без порч
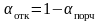 .
.
Вернёмся к анализу выражения (7.4)
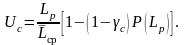
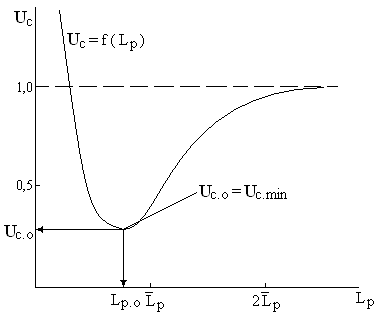 Анализ
этого выражения показывает, что затраты
Анализ
этого выражения показывает, что затраты
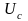 зависят
от типа закона распределения длительности
работы элемента (узла) до отказа, его
параметров и соотношения затрат
.
зависят
от типа закона распределения длительности
работы элемента (узла) до отказа, его
параметров и соотношения затрат
.
Рис.7.5. Схема определения оптимального межремонтного пробега
Относительные
суммарные затраты
являются целевой функцией, которую
необходимо минимизировать. Для определения
оптимального значения межремонтного
пробега
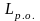 необходимо приравнять к нулю первую
производную
необходимо приравнять к нулю первую
производную
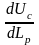 и решить полученное уравнение. Так как
оно получается трансцендентным и
довольно сложным, его решение возможно
графическими или численными методами,
в частности, с применением ЭВМ.
и решить полученное уравнение. Так как
оно получается трансцендентным и
довольно сложным, его решение возможно
графическими или численными методами,
в частности, с применением ЭВМ.
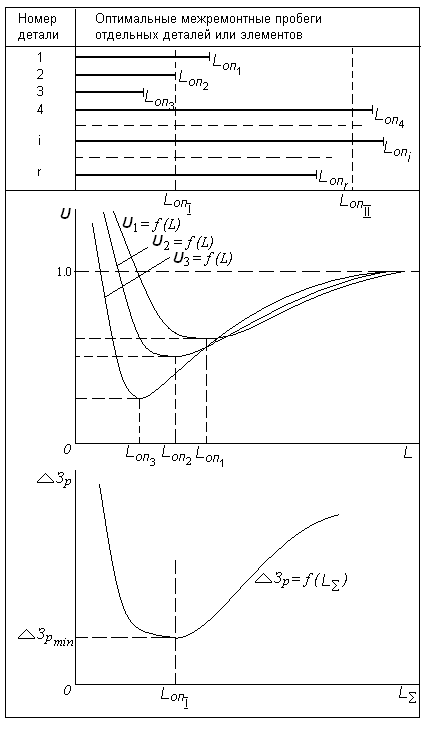
Рис. 7.6. Схема определения оптимального межремонтного пробега для группы деталей (элементов) локомотива
На
рис. 7.5 показано, что при
 затраты
затраты
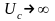 ,
а при
,
а при
 значение
имеет предел, равный единице, т.е. в этом
случае замена детали всегда будет
осуществляться на неплановом ремонте.
При этом точка минимума (
значение
имеет предел, равный единице, т.е. в этом
случае замена детали всегда будет
осуществляться на неплановом ремонте.
При этом точка минимума ( )
существует в том случае, если отношение
затрат
)
существует в том случае, если отношение
затрат
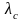 и коэффициент вариации длительности
работы до отказа
и коэффициент вариации длительности
работы до отказа
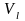 удовлетворяют условиям
удовлетворяют условиям
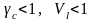 .
.
Годовой
экономический эффект от перехода на
оптимальное значение межремонтного
пробега
 в конкретных условиях эксплуатации для
узлов или элементов конструкции
локомотивов составит
в конкретных условиях эксплуатации для
узлов или элементов конструкции
локомотивов составит
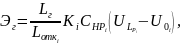
где
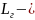 годовой пробег локомотивов;
годовой пробег локомотивов;
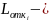 величина среднего пробега локомотива
до отказа детали или элемента конструкции;
величина среднего пробега локомотива
до отказа детали или элемента конструкции;
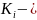 количество
деталей или элементов
количество
деталей или элементов
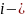 го
типа на локомотиве;
го
типа на локомотиве;
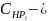 средние
затраты на выполнение непланового
ремонта деталей или элементов
средние
затраты на выполнение непланового
ремонта деталей или элементов
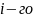 типа;
типа;
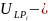 значение относительных затрат при
существующем межремонтном пробеге;
значение относительных затрат при
существующем межремонтном пробеге;
 значение относительных затрат при
оптимальном межремонтном пробеге.
значение относительных затрат при
оптимальном межремонтном пробеге.
Рассмотренный
метод позволяет определять оптимальную
продолжительность между плановыми
ремонтами
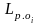 для
каждой детали или элемента конструкции
локомотива. Естественно, что они будут
различными. Поэтому для определения
оптимального межремонтного пробега
локомотива по нескольким критическим
элементам все детали или узлы можно
разделить на ряд групп с близкими
значениями
для
каждой детали или элемента конструкции
локомотива. Естественно, что они будут
различными. Поэтому для определения
оптимального межремонтного пробега
локомотива по нескольким критическим
элементам все детали или узлы можно
разделить на ряд групп с близкими
значениями
 .
Детали или элементы конструкции, вошедшие
в одну группу, следует восстанавливать
на одном виде ремонта, как показано на
рис. 7.6.
.
Детали или элементы конструкции, вошедшие
в одну группу, следует восстанавливать
на одном виде ремонта, как показано на
рис. 7.6.
С
этой целью определяют оптимальный
межремонтный пробег
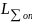 ,
общий для r
деталей или элементов, вошедших в одну
группу. Этот пробег должен соответствовать
минимуму суммарного увеличения затрат
из-за несовпадения общего межремонтного
пробега
с оптимальными межремонтными пробегами
для
каждой детали или элемента конструкции.
,
общий для r
деталей или элементов, вошедших в одну
группу. Этот пробег должен соответствовать
минимуму суммарного увеличения затрат
из-за несовпадения общего межремонтного
пробега
с оптимальными межремонтными пробегами
для
каждой детали или элемента конструкции.
Увеличение затрат при несовпадении межремонтных пробегов деталей (элементов) в группе определяется в виде

где
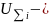 значение роста относительных затрат
для
ой детали при новом межремонтном пробеге
.
Обычно
значение роста относительных затрат
для
ой детали при новом межремонтном пробеге
.
Обычно
 .
.
Построив
зависимость
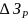 от величины
от величины
 ,
можно определить минимум
и соответствующее ему оптимальное
значение
,
можно определить минимум
и соответствующее ему оптимальное
значение
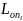 для деталей (элементов) первой группы
(см. рис. 7.6).
для деталей (элементов) первой группы
(см. рис. 7.6).
ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ МЕЖРЕМОНТНЫХ ПРОБЕГОВ
ЛОКОМОТИВОВ ИСХОДЯ ИЗ УСЛОВИЙ ОБЕСПЕЧЕНИЯ
ЗАДАННОГО УРОВНЯ ИХ БЕЗОТКАЗНОСТИ
 Рассмотренный
в предыдущем разделе технико-экономический
подход к определению величины оптимального
межремонтного пробега локомотивов и
их основных элементов, при
Рассмотренный
в предыдущем разделе технико-экономический
подход к определению величины оптимального
межремонтного пробега локомотивов и
их основных элементов, при
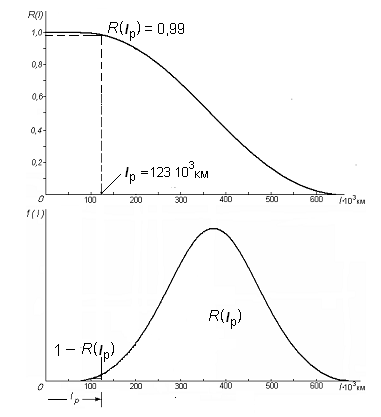
Рис. 7. 7. Определение допустимого межремонтного пробега при помощи кривой надёжности или функции плотности распределения наработки элементов конструкции на отказ
всей
своей универсальности, не учитывает
такой важный эксплуатационный фактор,
как требование высокой степени
безотказности определённой группы
элементов конструкции локомотивов
 в период между плановыми ремонтами или
техническими обслуживаниями.
в период между плановыми ремонтами или
техническими обслуживаниями.
В
период работы локомотивов между ТО-3
(наработка 7...8 тыс. км) или ТР-1 (наработка
30...40 тыс. км) вероятность их безотказной
работы должна быть близка к единице.
Если известна плотность распределения
наработки элемента или системы до отказа
,
а соответственно, и функция изменения
вероятности безотказной работы
,
то величина допустимого значения
межремонтного пробега элемента
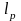 определяется
достаточно просто графически.
определяется
достаточно просто графически.
Таким образом, по условию задачи требуемая вероятность безотказной работы элемента (системы) конструкции локомотива должна быть задана. Определению подлежит величина . Решение подобной задачи оказывается аналогичной определению величины гамма-процентного ресурса локомотива и элементов его конструкции.
Так,
если мы располагаем функциями
или
,
и нам задана требуемая величина
вероятности безотказной работы элемента,
например,
= 0,99, то допустимая величина наработки
элемента конструкции составляет
 , как показано на рис. 7.7.
, как показано на рис. 7.7.
ТЕМА 8
