Общим уравнением прямой

О

12

пределение 1. Прямой линией на плоскости называется множество всех точек М(х;у), координаты которых удовлетворяют уравнению , где А, В, С – заданные числа, причем А и В не равны нулю одновременно. Уравнение (4.1) называется общим уравнением прямой на плоскости. Пусть точка лежит на прямой, т.е. ее координаты удовлетворяют уравнению . Вычитая это равенство из (4.1), получим . Пусть вектор .Поскольку вектор , (4.2) можно записать с помощью скалярного произведения векторов и в виде . Отсюда следует, что векторы и перпендикулярны. Вектор лежит на данной прямой, поэтому вектор перпендикулярен этой прямой. Таким образом, мы получили геометрический смысл коэффициентов А и В общего уравнения прямой на плоскости (4.1): коэффициенты А и В общего уравнения прямой на плоскости – это координаты вектора, перпендикулярного данной прямой. Поэтому уравнение (4.2) – это уравнение прямой на плоскости, проходящей через данную точку перпендикулярно данному вектору .

Уравнения и иногда называют неполными уравнениями прямой.

Если С = 0, то получаем уравнение , которое проходит через начало координат, так как координаты точки О(0;0) удовлетворяют этому уравнению.

Пусть теперь . Преобразуем уравнение (4.1) следующим образом: 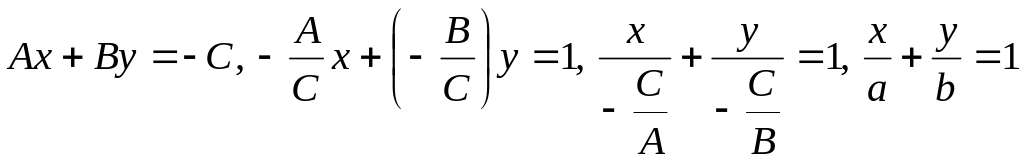, где . Это уравнение прямой, которое имеет специальное название.

Определение 2. Уравнение прямой вида называется уравнением прямой в отрезках. Уравнение прямой в отрезках удобно при построении прямой, так как прямая, очевидно, проходит через точки (а;0) и (0;b) осей координат, т.е. отсекает на осях координат соответствующие отрезки.

Каноническим уравнением

В

13

ыведем теперь уравнение прямой, проходящей через данную точку и параллельной данному вектору . Если точка М(х,у) лежит на прямой, то вектор тоже лежит на этой прямой и коллинеарен данному вектору . Поэтому координаты этих векторов пропорциональны, т.е. - искомое уравнение прямой.

Определение 3. Уравнение прямой вида

(4.4)

называется каноническим уравнением прямой на плоскости, проходящей через точку . Вектор называется направляющим вектором прямой.

Обозначив общее значение дробей в уравнении буквой t, т.е. положив = t, получим .

Определение 4. Уравнение прямой вида

, (4.5)

называется параметрическим уравнением прямой, проходящей через точку в направлении вектора . Параметр .

Пусть в общем уравнении прямой . Решим его относительно у: . Обозначив , получим . Определение 5. Уравнение прямой вида называется уравнением прямой с угловым коэффициентом. Коэффициент k называется угловым коэффициентом прямой.

Найдем угловой коэффициент прямой, проходящей через две точки и . Координаты этих точек удовлетворяют уравнению прямой, т.е. и . Вычитая из второго равенства первое, получим и . Из рисунка видим, что , где α – угол наклона -уравнение прямой, проходящей через две заданные точки и , .

- уравнение прямой, проходящей через две заданные точки и , .

14

Получим теперь формулы для вычисления угла между двумя прямыми. Если прямые заданы общими уравнениями и , то, очевидно, угол между ними равен углу между векторами и , перпендикулярными данным прямым. Поэтому и

. (4.8)

Если прямые перпендикулярны, то угол , и

. (4.9)

Если же прямые параллельны, то векторы и коллинеарны, поэтому

(4.10)

Таким образом, нами получены условие перпендикулярности (4.9) и параллельности (4.10) прямых, заданных общими уравнениями.