Скалярное произведения векторов
С
9
,
равное произведению длин этих векторов
и косинуса угла между ними:
=
.
Поскольку
пр
,
а
пр
получаем, что
=
пр
=
пр
.
Свойства скалярного произведения:
,
(3.2)
,
(3.3)
.
(3.4)
Равенство (3.2)
=
=
.
Равенства (3.3) и (3.4) доказываются с помощью формул (2.1) и (2.3):
пр
=
пр
+
пр
=
,
пр
пр
=
.
Из (3.2) и (3.3) имеем
,
,
а из (3.2) и (3.4):
,
(3.6) поскольку
.
Для того, чтобы
записать скалярное произведение в
координатной форме, обозначим через
единичные векторы координатных осей
Ох,
Оу,
Оz
в пространстве соответственно. Очевидно,
что
.
Поэтому
,
т.е. любой вектор
можно записать в виде
=
.
Заметим также, что для скалярных
произведений векторов
справедливы равенства
,
.
Пусть теперь
.
Тогда по свойствам (3.2) – (3.6) скалярного
произведения имеем
.
Таким образом,
.
(3.7) В частном случае при
получаем
,
поэтому длина вектора
равна
.
С помощью формулы
(3.8) можно получить формулу для вычисления
расстояния между точками
и
.
Расстояние АВ
равно длине вектора
,
где
и
- радиус-векторы точек А
и В
соответственно.
(3.9)
Пример 1.
Найдем скалярное произведение векторов
и
и
угол между ними.
Решение.
По формуле (3.7)
,
по формуле (3.8)
из формулы (3.1) находим
,
.
Пример 2. Найдем расстояние между точками А(2,3,6) и В(1,0,–2).
Решение.
По формуле (3.9) находим
.
Векторное произведение векторов
В
10
и
называется вектор
.
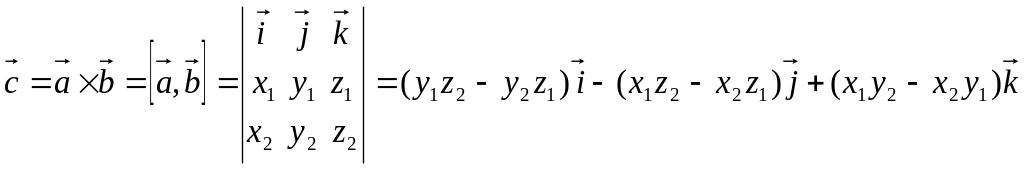(3.10)
Другое определение, равносильное данному определению.
Векторным произведением двух векторов и называется вектор , удовлетворяющий следующим условиям:
1) если векторы и коллинеарны, то = 0;
2) если векторы
и
не коллинеарны, то вектор
перпендикулярен векторам
и
и
направлен так, что система
ориентирована так же, как и данная
система координат. Длина вектора
,
длина вектора
= S
параллелограмма.
Рассмотрим свойства векторного произведения.
1)
2)
3)
где
- произвольные векторы, α – число.
Все эти свойства получаются из формулы (3.10) и свойств определителя.
;
;
.
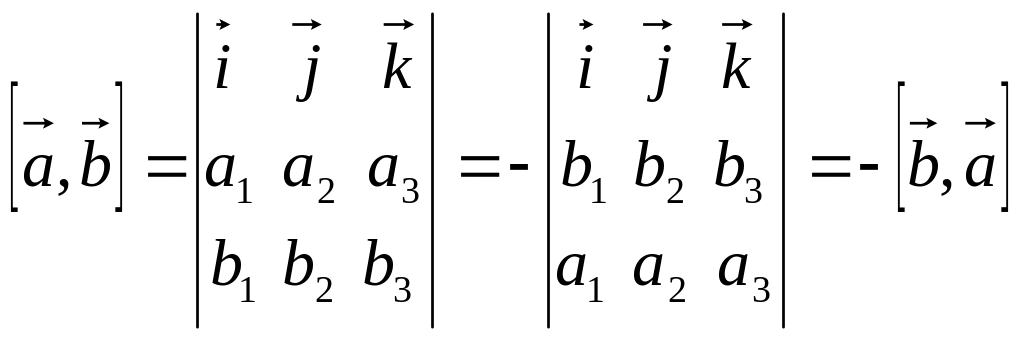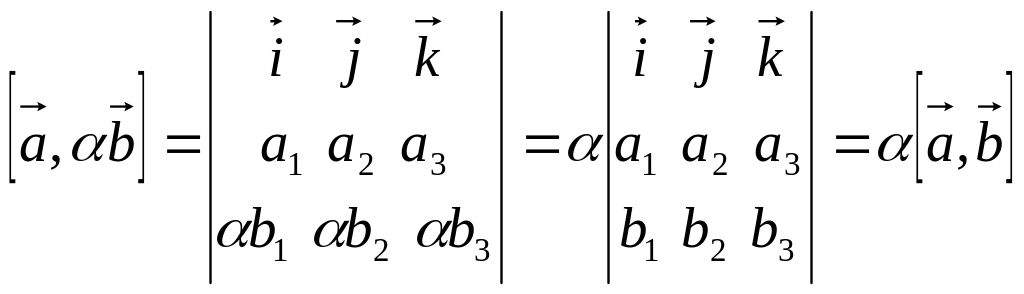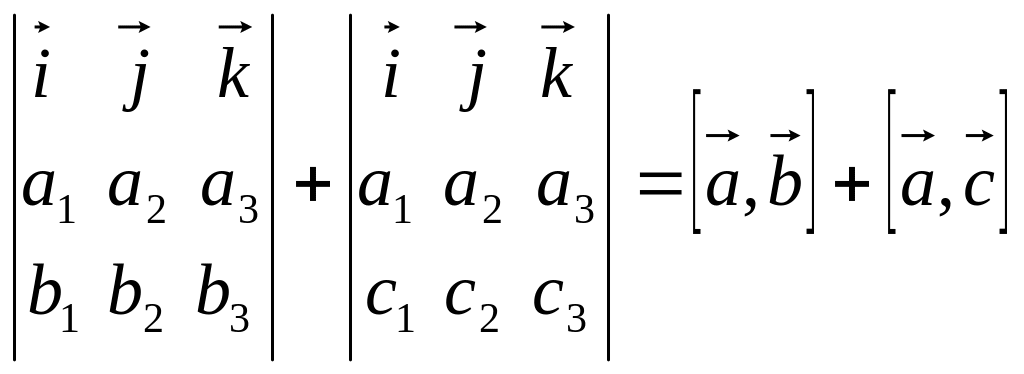Пример 5. На плоскости даны три точки А(1;2), В(–1;3), С(0;–2). Найдем площадь параллелограмма, сторонами которого являются отрезки АВ и АС.
Решение. По
определению 3 площадь параллелограмма,
построенного на векторах
и
,
равна длине вектора
,
являющегося векторным произведением
векторов
и
.
Поэтому нам нужно найти длину вектора,
являющегося векторным произведением
векторов
и
.
Чтобы найти векторное произведение
векторов
и
воспользуемся формулой (3.10). Найдем
координаты этих векторов:
,
(третья
координата равна нулю, так как векторы
находятся в плоскости
).
Тогда
=
,
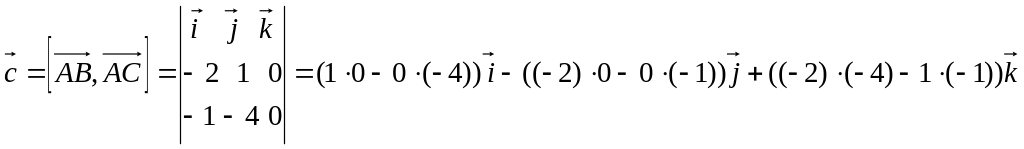т.е. искомая площадь параллелограмма
равна 9.
Из равенства
(3.10) получаем, что одновременно
,
и
.
Отсюда
,
и
,
,
т.е.
.
Таким образом, получаем, что векторы
коллинеарны тогда и только тогда, когда
их координаты пропорциональны.
Смешанным
(векторно-скалярным) произведением
трех
векторов
,
и
называется число, равное скалярному
произведению вектора
на вектор
.
Обозначается
.
П
11
.По
формулам (3.10) и (3.7), определению определителя
2-го порядка и формуле разложения
определителя 3-го порядка по элементам
третьей строки имеем
=
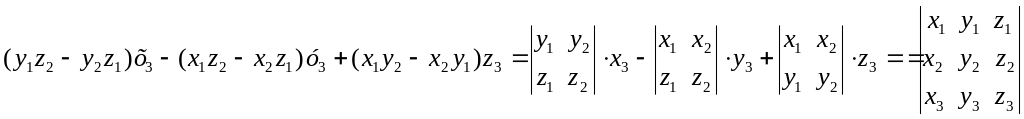Таким
образом, смешанное произведение трех
векторов вычисляется по формуле
=
.
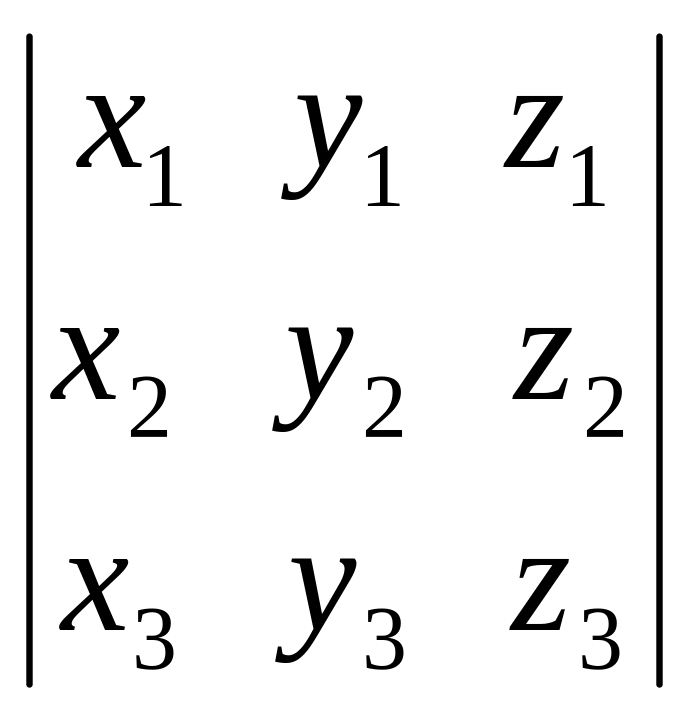В силу определения скалярного
произведения
=
пр
.
Поскольку │пр
│-
высота параллелепипеда, построенного
на векторах
,
и
,
в основании которого лежит параллелограмм,
имеющий площадь
,
то │
│-
объем этого параллелепипеда. Таким
образом, модуль смешанного произведения
векторов
,
и
равен объему параллелепипеда, построенного
на этих векторах.
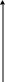
пр
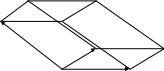
Если векторы
,
,
лежат в одной плоскости, то векторы
и
перпендикулярны, поэтому
= 0. Обратно, если
= 0, то
,
поэтому
,
и
лежат в одной или параллельных плоскостях.
Таким образом, условие
= 0 является необходимым и достаточным
условием компланарности трех векторов
,
и
.
Свойства смешанного произведения:
1. Смешанное
произведение не изменяется при циклической
перестановке перемножаемых векторов:
=
=
.
Это следует из свойства б) определителя:
=
=
,
=
=
.
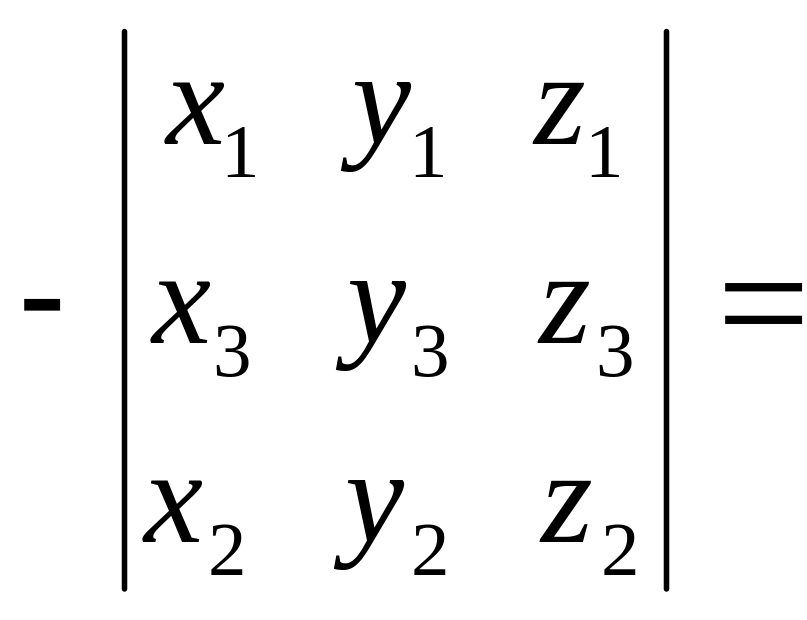
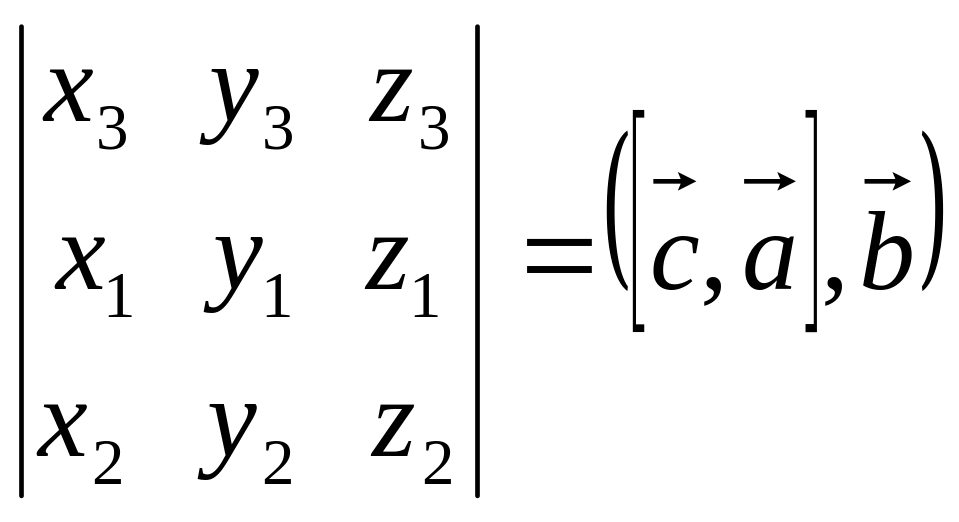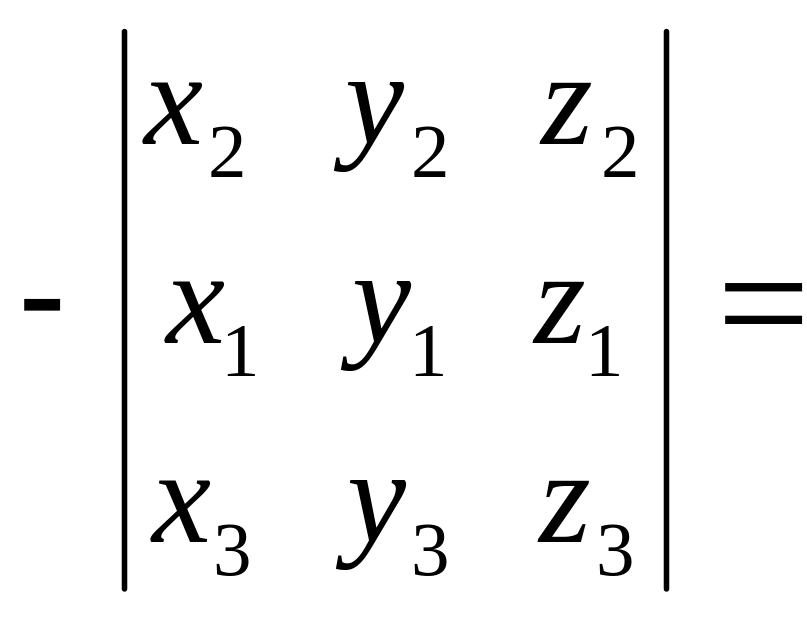
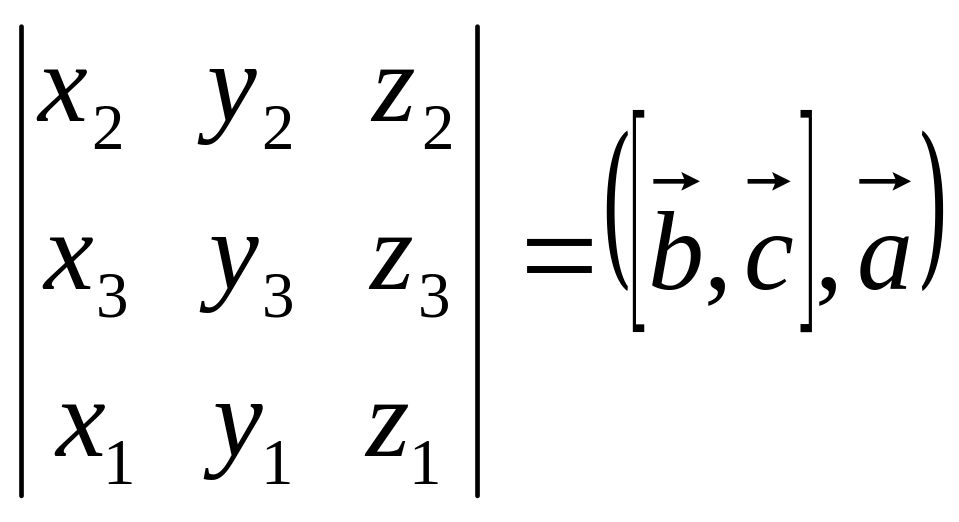2. Смешанное произведение меняет знак при перестановке двух векторов, например,
=
.
Это следует из того же свойства б)
определителя.