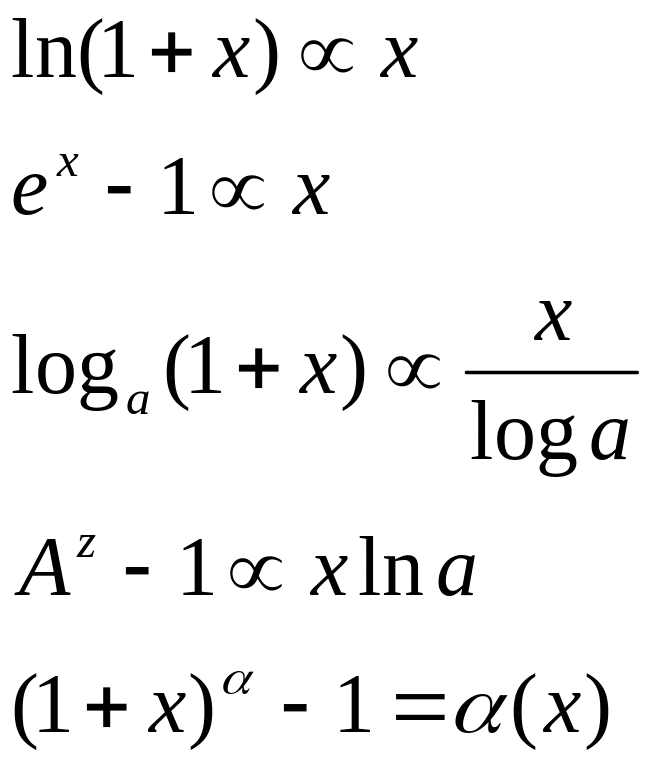Предел функции по Гейне

З

27

начение называется пределом (предельным значением) функции в точке , если для любой последовательности точек , сходящейся к , но не содержащей в качестве одного из своих элементов, последовательность значений функции сходится к .

Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (преде́лом спра́ва).

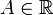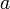• Число называется правосторонним пределом (правым пределом, пределом справа) функции в точке , если для всякой последовательности , состоящей из точек, больших числа , которая сама сходится к числу , соответствующая последовательность значений функции сходится к числу .

• Число называется левосторонним пределом (левым пределом, пределом слева) функции в точке , если для всякой последовательности , состоящей из точек, меньших числа , которая сама сходится к числу , соответствующая последовательность значений функции сходится к числу .

Теорема19.4(арифметические операции над функциями, имеющими предел).

Если существуют  и  то существуют конечные пределы     , если , причем   ,               (19.1).

Бесконечно малая величина

П

28

оследовательность a_n называется бесконечно малой, если . Например, последовательность чисел  — бесконечно малая.

Функция называется бесконечно малой в окрестности точки x₀, если .

Функция называется бесконечно малой на бесконечности, если либо .

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если , то f(x) − a = α(x), .

Бесконечно большая величина

Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция xsinx, неограниченная с обеих сторон, не является бесконечно большой при .

Последовательность a_n называется бесконечно большой, если .

Функция называется бесконечно большой в окрестности точки x₀, если .

Функция называется бесконечно большой на бесконечности, если либо .

Свойства бесконечно малых

• Сумма конечного числа бесконечно малых — бесконечно малая.

• Произведение бесконечно малых — бесконечно малая.

• Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.

• Если a_n — бесконечно малая последовательность, сохраняющая знак, то 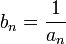— бесконечно большая последовательность.

Определения

Допустим, у нас есть бесконечно малые при одном и том же величины α(x) и β(x) (либо, что не важно для определения, бесконечно малые последовательности).

• Если 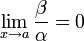, то β — бесконечно малая высшего порядка малости, чем α. Обозначают β = o(α).

• Если 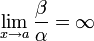, то β — бесконечно малая низшего порядка малости, чем α. Соответственно α = o(β).

• Если 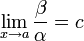(предел конечен и не равен 0), то α и β являются бесконечно малыми величинами одного порядка малости. Это обозначается как β = O(α) или α = O(β) (в силу симметричности данного отношения).

• Если 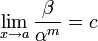(предел конечен и не равен 0), то бесконечно малая величина β имеет m-й порядок малости относительно бесконечно малой α.

Для вычисления подобных пределов удобно использовать правило Лопиталя

1-й и 2-й замечательный придел

29

Называется бесконечно малой (б м) функцией в окрестности точки Х₀ если

Например - б м функция в окрестности точки А т.к.

Для того что бы необходимо и достаточно чтобы имело место представления где б м в окрестности точки Х₀ функция. Пример

Второй замечательный придел

Справедливо равенство

Обозначим если то Второй замечательный придел имеет вид

Следствие

1. Придел предел отношения 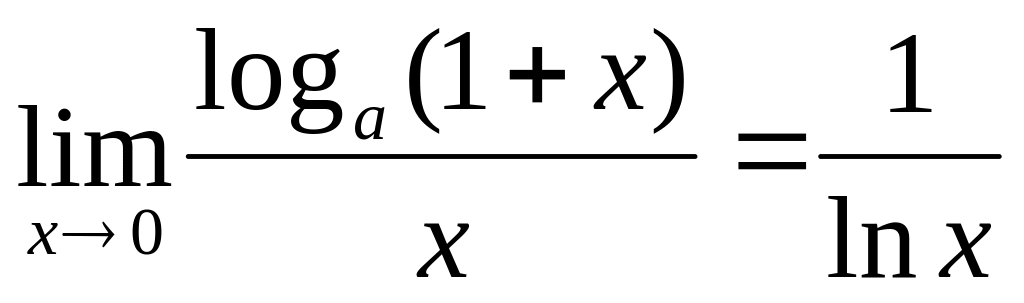В частности

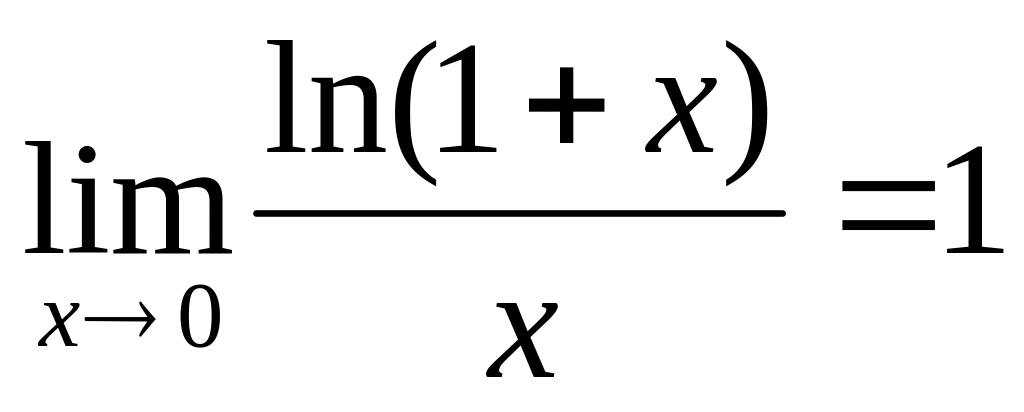
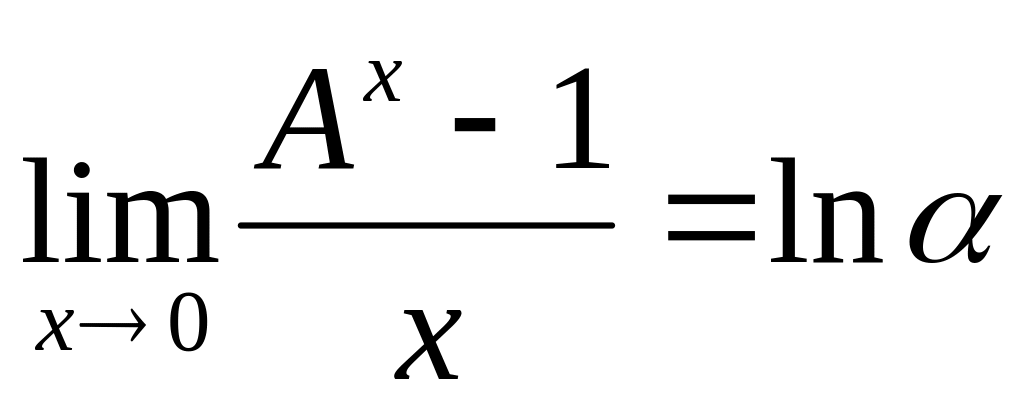2. в частности

3. 

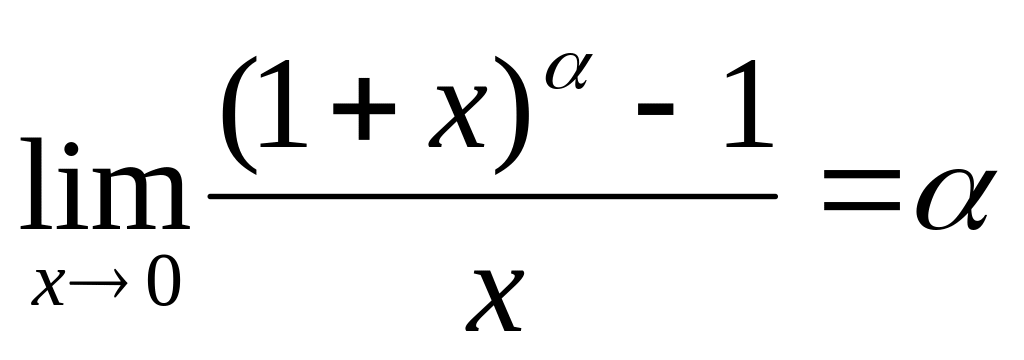
Пример

Из следствий имеем :