
- •М 1 атрицы
- •Определители матриц
- •Системы линейных алгебраических уравнений
- •Обратная матрица
- •Размерность. Базис. Линейное подпространство
- •Векторы. Линейные операции над векторами
- •Прямоугольная (декартова) система координат
- •Скалярное произведения векторов
- •Векторное произведение векторов
- •Общим уравнением прямой
- •Каноническим уравнением
- •Угол между двумя прямыми
- •Окружность и эллипс
- •Угол между двумя плоскостями
- •Каноническое и параметрическое уравнение прямой в пространстве
- •Угол между прямей и плоскостью
- •Числовая последовательность
- •Свойства сходящихся последовательностей
- •Предел функции по Гейне
- •Бесконечно малая величина
- •Бесконечно большая величина
- •Свойства бесконечно малых
- •Определения
- •Непрерывность функции в точке и на множестве
- •Классификация разрывов.
М 1 атрицы
Определение 1.
Прямоугольная таблица чисел
![]() вида
вида
А
=

![]() ,
,
состоящая из m
строк и n
столбцов,
называется матрицей
размера
![]() .
Числа
называются ее элементами.
Матрица размера
.
Числа
называются ее элементами.
Матрица размера
![]() называется матрицей-столбцом,
размера
называется матрицей-столбцом,
размера
![]() -
матрицей-строкой,
размера
-
матрицей-строкой,
размера
![]() - квадратной
матрицей n-го
порядка.
- квадратной
матрицей n-го
порядка.
Определение 2.
Две матрицы
![]() и
и
![]() называются равными, если они имеют
одинаковые размеры
и их соответствующие элементы равны:
называются равными, если они имеют
одинаковые размеры
и их соответствующие элементы равны:
![]() .
.
Единичной
матрицей
называется квадратная матрица вида

диагональной
матрицей
(
=0,
если
![]() ),
а матрица вида
),
а матрица вида
 -
-
треугольной
матрицей
(
=
0, если
![]() ).
Прямоугольная матрица размера
).
Прямоугольная матрица размера
![]() называется
ступенчатой,
если она имеет вид
А =
называется
ступенчатой,
если она имеет вид
А =

Определение 4.
Матрица
![]() называется транспонированной
к матрице
называется транспонированной
к матрице
![]() ,
если она получена из матрицы А
заменой ее
столбцов строками с теми же
,
если она получена из матрицы А
заменой ее
столбцов строками с теми же
номерами, т.е. если
![]() .
.
Таким образом,
транспонированная к матрице А
размера
матрица
![]() имеет вид
имеет вид
=
 и размер
и размер
![]() .
.
Определение
5. Суммой
(разностью)
двух матриц
и
![]() размера
называется матрица размера
размера
называется матрица размера
![]() ,
элементы которой равны сумме (разности)
соответствующих элементов матриц А
и В
.
,
элементы которой равны сумме (разности)
соответствующих элементов матриц А
и В
.
Определение
6. Произведением
матрицы
на число
![]() называется матрица
называется матрица
![]() ,
элементы которой равны произведению
числа
на соответствующие элементы матрицы
А.
,
элементы которой равны произведению
числа
на соответствующие элементы матрицы
А.
Определители матриц
2
Определение
1. Определителем
квадратной
матрицы А
=
![]() 1-го порядка (определителем 1-го порядка)
называется число, обозначаемое
1-го порядка (определителем 1-го порядка)
называется число, обозначаемое
![]() и равное
и равное
![]() .
Определителем квадратной матрицы 2-го
порядка называется число
.
Определителем квадратной матрицы 2-го
порядка называется число
![]() .
.
Таким образом, определители 2-го и 3-го порядков являются алгебраическими суммами (т.е. суммами и разностями) всевозможных произведений элементов из каждой строки и каждого столбца определителя, причем из каждой строки и каждого столбца берется по одному элементу.
Определение
2.Величина
![]() ,
равная произведению определителя (n
– 1)-го порядка
,
равная произведению определителя (n
– 1)-го порядка
![]() ,
полученного из определителя n-го
порядка вычеркиванием i-ой
строки и k-го
столбца, на число
,
полученного из определителя n-го
порядка вычеркиванием i-ой
строки и k-го
столбца, на число
![]() ,
называется алгебраическим
дополнением элемента
,
называется алгебраическим
дополнением элемента
![]() .
.
Установим теперь свойства определителей.
Величина определителя:
а) не меняется, если у него заменить строки соответствующими столбцами.
б) меняет знак при перемене местами любых двух строк или любых двух столбцов.
в) умножается на число k, если элементы какого-либо его столбца или строки умножить на k.
г) равна нулю, если элементы какого-либо его столбца или строки равны нулю.
д) равна нулю, если элементы двух строк или столбцов соответственно равны.
е) Разложение Лапласа: сумма произведений элементов некоторой строки или столбца определителя на алгебраические дополнения этих элементов равна величине определителя:
![]() ,
,
![]() .
.
Докажем это свойство
для определителя третьего порядка в
случае третьей строки. Имеем
![]()
![]()
![]() .
.
Пример
1.
 .
.
Пример
2. Если все элементы определителя
![]() ,
стоящие ниже (или выше) главной диагонали,
равны нулю, то
,
стоящие ниже (или выше) главной диагонали,
равны нулю, то
![]() .
.
Таким образом, определитель треугольной матрицы равен произведению элементов, стоящих на главной диагонали.
ж)
Сумма произведений элементов
некоторой строки (столбца) определителя
на соответствующие алгебраические
дополнения элементов другой строки
(столбца) равна нулю:
![]() .
.
з
2![]() и
и
![]() ,
у которых все строки (столбцы) одинаковы,
кроме одной строки (одного столбца).
Сумма таких определителей равна
определителю n-го
порядка, у которого указанная строка
(столбец) состоит из суммы соответствующих
элементов этой строки (столбца)
определителей
и
.
,
у которых все строки (столбцы) одинаковы,
кроме одной строки (одного столбца).
Сумма таких определителей равна
определителю n-го
порядка, у которого указанная строка
(столбец) состоит из суммы соответствующих
элементов этой строки (столбца)
определителей
и
.
и) Величина определителя не изменится, если к элементам какой-либо его строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на число k .
(Иллюстрировать лучше на примере определителя 3-го порядка)
Пример
4. Вычислим определитель Вандермонда
4-го порядка
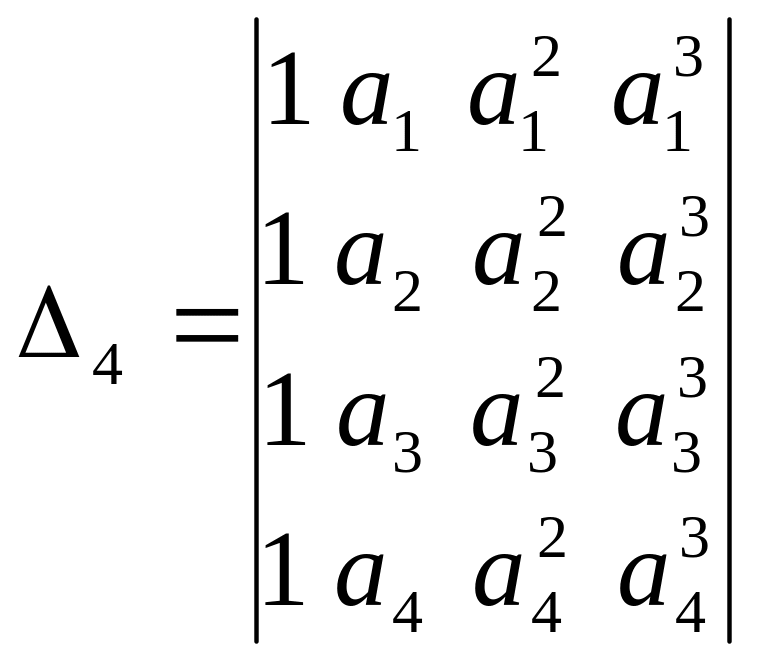 (А.Т. Вандермонд (1735-1796) – французский
математик).
(А.Т. Вандермонд (1735-1796) – французский
математик).
Решение. Вычтем
из элементов 2-ой, 3-ей и 4-ой строк
соответствующие элементы 1-ой строки,
получим
 .
Вынесем за знак определителя общие
множители 2-ой, 3-ей и 4-ой строк (свойство
в)), затем вычтем из элементов 3-ей и 4-ой
строк полученного определителя
соответствующие элементы 2-ой строки:
.
Вынесем за знак определителя общие
множители 2-ой, 3-ей и 4-ой строк (свойство
в)), затем вычтем из элементов 3-ей и 4-ой
строк полученного определителя
соответствующие элементы 2-ой строки:
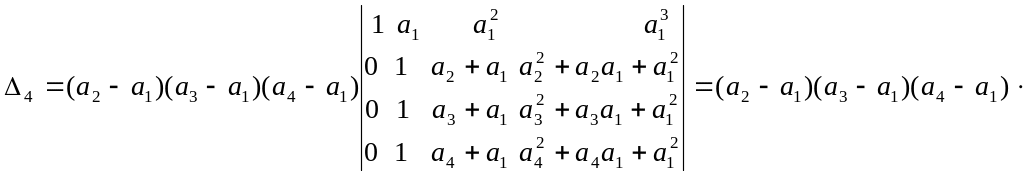
 .
Вынесем за знак определителя общие
множители 3-ей и 4-ой строк, затем вычтем
из элементов 4-ой строки полученного
определителя соответствующие элементы
3-ой строки:
.
Вынесем за знак определителя общие
множители 3-ей и 4-ой строк, затем вычтем
из элементов 4-ой строки полученного
определителя соответствующие элементы
3-ой строки:

 .
.
Получился
определитель треугольного вида, величина
которого равна произведению элементов
главной диагонали (см. пример 2), т.е.
![]() .
Поэтому
.
Поэтому
![]() .
.
