12. Охарактеризовать системы образующих и базисы векторного пространства. Дать определение размерности векторного пространства.

Пусть V – векторное пространство. 1)Линейной комбинацией векторов 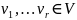называется вектор 2) Векторы называются линейно зависимыми, если , где хотя бы одно из чисел не равно нулю. В противном случае векторы называются линейно независимыми. Теорема. Системы векторов линейно зависима, если и только если один из векторов является линейной комбинацией векторов - линейно зависимы  )  => в линейном пространстве V существует минимальная независимая система векторов, к-рая облад.св-вами:

1) – линейно независимы

2) любой вектор выражается в виде линейной комбинации вектора Базисом линейного векторного пространства V называется максимальная система векторов, обладающих с-вами 1 и 2. Число векторов базиса называется размерностью векторного пространства и обозначается dimV (dimension) Базис - система векторов, таки что 1) - линейно независимы, 2) + 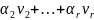Пример. Арифметическое n-мерное лин.пр-во. ℝⁿ=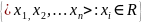 V₁+V₂= <x₁,x₂,…x_n> +<y₁,y₂,…y_n> α*V=α < αx₂,…,αx_n> ℝⁿ – линейное пространство с Ō=<0,0…0> Базисом этого пространства является набор векторов 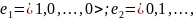0>; Любой вектор v=<x₁,…,x_n> v=x₁e₁+x₂e₂+…+x_ne_{n dimℝ}ⁿ=n Часто n-мерные векторы как упорядоченные наборы n чисел Любой из векторов ⁿ можно получить в виде линейной комбинации базисных векторов, т.е.

13.Охарактеризовать действие скалярного произведения векторов в арифметическом n-мерном векторном пространстве

Скалярным произведением двух векторов V=<x₁,x₂,…x_n> и W=<y_1,y₂,…,y_n> называется число, равное сумме произведений компонент этих векторов, т.е. коэффициентов их выражения через базис. Обозначается VW=V*W=x₁y₁+x₂y₂+…+x_ny_n Из определения вытекают следующие свойства 1) VW=WV 2)(V₁+V₂)W = V₁W+ V₂W 3)если α – некоторое число, то α(WV) = (αW)V=(αV)W Если W*V=0, то говорят, что векторы W и V ортогональны и пишут V┴W Нормой (длиной) вектора V называется число |V|= Норма обладает след.св-вами |V| 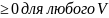|V|=0, если V=Ō=<0,0,0,….,0> 3) Если α 4) Неравенство Коши-Буняковского |WV|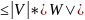 5) Неравенства треугольника (для любых V и W |-|W|| Линейное пространство векторов V, в котором определено скалярное произведение векторов, удовлетворяющ. перечисленным выше св-вам называют Евклидовым пространством.

14.Дать определение свободного вектора на плоскости(в пространстве).

Свободным вектором а=АВ с представителями АВ называют множество всех векторов равнонаправленных с данными, те классами эквивалентности для АВ. Свободный вектор – который потенциально может быть помещён в любую точку пространства.а=АВ=СD.(ПРОСТРАНСТВО)

Длинной и направлением свободного вектора а=АВ называют длинной направлением его представителя. Свободный вектор а=АВ, b=CD называют одинаково противоположено направленные или коллинеарными, если этим свойством обладают какие либо другие 2 их представителя. (плоскость)

15.Дать понятие ортонормированного базиса и ориентации базиса. Как определяются прямоугольные координаты вектора.

Базислм векторов на плоскости называют любую пару ˂а₁а₂˃ некоторых векторов. Базисом векторов в пространстве называют любую тройку _{˂а1а2а3˃.} Ортогональным базисом называют базис, состоящий из взаимно ортогональных единичных векторов. Классы одноимённых базисов называют ориентациями. На прямой на плоскости и в пространстве существуют точно две различные ориентации:базисы принадлежащие одной и той же ориентации, -одноименны, и базисы принадлежащие различным ориентациям, разноимённы.

17. описать геометрические применения скалярного, векторного и смешанного произведения векторов.

Использование скалярного произведения крайне широко, как в элементарных, так и в весьма абстрактных областях математики, физики и прикладных наук.

Широко известны следующие применения: Любые геометрические вычисления (как собственно в математике, так и в приложениях), связанные с длинами, углами, проецированием, ортогональностью. Например, теорема косинусов легко выводится с использованием скалярного произведения:

Угол между векторами:

18.Дать определение прямоугольной матрицы, равенства матриц, транспонированной матрицы. Как определяются и выполняются действия умножения матрицы на число ,сложение, вычитание и умножение матриц? Матрицей (прямоугольной mхn матрицей, где m,n ) называется прямоугольная таблица, составленная из элементов a_{ij ,} расположенных в m строк и n столбцов. 1хn матрица (а₁,а₂,…,а_n)-строка размера n 1хm матрица -столбец размера m. Матрица обозначается A=A_mxn=(a_ij)_mxn= Матрицы А=(a_ij)_mxn и В=(b_ij)_pxqm=p,n=q и a_ij=b_ij для любых ij Действие ТРСПН матрицы А состоит в расположении строк этой матрицы в столбцы с теми же номерами. В рез-те получается nxm матрица, обозначаемая А^Т_nxm (А_mxn)^T=(A^T)_nxm Пример 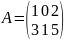=>A^T Умножение матрицы на число Произведение mxn матрицы А на число (скаляр) α называется новая mxn матрица из А умножение всех ее элементов на число α Сложение (вычитание) матриц Складывать и вычитать можно только матрицы одинаковых размеров. Пусть А=А_mxn и В=В_mxn. Тогда суммой(разностью), обозначаемой называется новая mxn матрица, составленная из сумм (разностей) элементов, стоящих на соответствующих местах. Пример. А= и В А+В = = А= и В А-В = = Умножение матриц Пусть А=(a_ij)_mxp и В =(b_ij). Операция умножения матрицы А на матрицу В определена, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц А*В называется такая матрица С, каждый элемент с_ij которой равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В. c_ij=a_i1b_1j+a_i2b_2j+…+a_ikb_kj

19.Охарактеризовать множество квадратных матриц одного порядка как алгебру. Единичная матрица и её роль в алгебре матриц.

Множество квадратных матриц одного порядка n обозначается M(n). На этом множестве определяются все действия введённые для матриц. Алгебраическая система:˂M(n),+,F(письменная)= кружок внутри точка, точка˃ является одновременно линейным пространством по отношению K+и F(письменная без палочки в другую сторону)=кружочек внутри с точкой. Едини́чная ма́трица — квадратная матрица, элементы главной диагонали которой равны единице поля, а остальные равны нулю.

Квадратная матрицаEn = (eij) размера (порядка n), где eii = 1 для всякого и eij = 0 для всяких назвается единичной матрицей порядка n. Единичная матрица размера обычно обозначается En и имеет вид: Произведение любой матрицы и единичной матрицы подходящего размера равно самой матрице:AE = EA = A

Квадратная матрица в нулевой степени дает единичную матрицу того же размера:A(в степени)0 = E.При умножении матрицы на обратную ей тоже получается единичная матрица: Единичная матрица получается при умножении ортогональной матрицы на ей транспонированную:AA(в степени T) = E. Определитель единичной матрицы равен единице:

20. Дать определение обратимой матрицы. Описать метод Гауса-Жордана вычисления обратной матрицы с помощью элементарных преобразований.

Квадратная матрица A называется обратимой, если существует такая матрица X, чтоAX=XA=E.

Матрица X называется обратной к матрице A и обозначается A -1, т.е. A A -1 =A -1A=E.

Известно, что если матрица A невырождена (т.е ее определитель отличен от нуля), то у нее существует обратная матрица A -1.Верно соотношение: (A-1)T =(AT ) -1.

Метод гауса.

(в тетрадке)

21.(в тетрадке)

22.сформулировать теорему об алгебраических дополнениях элементов строки определителя и объяснить её роль для его вычисления.

23.описать постановку задачи исследования и решения системы линейных линйных алгебраических уравнений с несколькими неизвестными. Описать различные формы записи системы линейных уровнений.(в тетрадке)

24.охарактеризовать способ исследования и решения системы линейных уравнений с помощью определителей. Вывести формулы крамера.(в тетрадке)

25.описать матричный способ решения системы линейных уравнений.(в тетрадке)

26.описать способы исследования и решения систем линейных уравнений с помощью элементарный преобразований(метод гауса жордана)

Алгоритм решения систем уравнений методом Жордана-Гаусса состоит из ряда однотипных шагов, на каждом из которых производятся действия в следующем порядке:

Проверяется, не является ли система несовместной. Если система содержит противоречивое уравнение, то она несовместна.

Проверяется возможность сокращения числа уравнений. Если в системе содержится тривиальное уравнение, его вычеркивают.

Если система уравнений является разрешенной, то записывают общее решение системы и если необходимо — частные решения.

Если система не является разрешенной, то в уравнении, не содержащем разрешенной неизвестной, выбирают разрешающий элемент и производят преобразование Жордана с этим элементом.

Далее заново переходят к пункту 1.

Пример

Решение:

Вычисления приведены в нижеследующей таблице:

Справа от таблицы изображены действия над уравнениями. Стрелками показано к какому уравнению прибавляется уравнение с разрешающим элементом, умноженное на подходящий множитель.

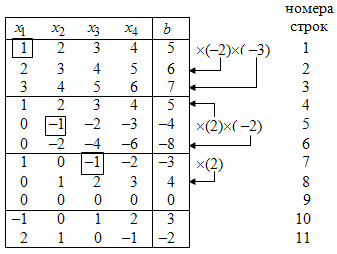В первых трех строках таблицы помещены коэффициенты при неизвестных и правые части исходной системы. Результаты первого преобразования Жордана с разрешающим элементом равным единице приведены в строках 4, 5, 6. Результаты второго преобразования Жордана с разрешающим элементом равным (-1) приведены в строках 7, 8, 9. Так как третье уравнение является тривиальным, то его можно не учитывать. Равносильная система с разрешенными неизвестными имеет вид:

Теперь можем записать Общее решение:

Приравниваем свободные переменные нулю и получаем: В нашем случае выбран разрешающий элемент (-1) в первом уравнении при строка 7). Далее производим преобразование Жордана. Получаем новую разрешенную систему (строки 10,11) c новыми разрешенными неизвестными

Записываем второе общее решение:

Ответ .