7. Дать определение бинарного отношения, его проекций и сечений. Описать основные способы представления бинарных отношений.

Понятие бинарное отношение является одним из основных понятий широко применяемых в математике.

Пусть А и В – два подмножества, АхВ – прямое (декартово) произведение этих множеств.

Бинарным отношением или соответствием между элементами множеств А и В называется любое подмножество их прямого произведения. Пусть х А, у В – переменные, принимающие значения в А и В. Говорят, что упорядоченная пара <x;y> представляет собой пару элементов, находящихся между собой в отношении R, если <x;y> R. В этом случае пишут также xRy.

Пусть R АхВ – некоторое бинарное отношение.

Первой проекцией бин.отн. R АхВ наз-ся множ-во pr₁R

Второй проекцией R наз-ся множ-во pr₂R

pr₁R=pr₁R^-1

pr₂R^-1=pr₂R

Сечением бинарного отношения R через элемент х называется множество

R(x) =

Обратным сечением называется множ-во R^-1(y)=

Основные способы представления бинарных отношений

1)перечисление всех его элементов 2)графический способ – способ представления, при кот-м каждой паре <x_i;y_j> ставится стрелка представл.данной паре система стрелок (диаграмма Бежа)

3)матричный – каждой паре <x_i;y_j> ставится в соответствие клетка со значением 0, если <x_i;y_j> R и ставится 1, если <x_i;y_j> R

4) способ сечения R:

8.Охарактеризовать рефлексивные, симметричные, транзитивные бинарные отношения. Привести примеры отношений обладающими такими свойствами. Говорят, что R является БО на множестве А если RcАхА=А(в квадрате). Для БО на множестве А рассматриваются следующие свойства. Рефлексивность – говорят что БО RcАхА рефлексивны если (А(верх ногами)х принадлежит А)˂х,х˃ принадлежит R , те хRх. Примеры: отношение равенства отношение сравнимости по модулю,отношение параллельности прямых и плоскостейотношение подобия геометрических фигур;отношения нестрогого порядка:отношение нестрогого неравенства, отношение нестрогого подмножества, отношение делимости. Семмитричность – БО отношения RcАхА называют семмитричными если ((А(вверх ногами)ху)хRу=˃уRх). R=R(-1 степени). Примеры: отношение равенства ,отношение сравнимости по модулю,отношение равномощности множеств,отношение параллельности прямых и плоскостей,отношение подобия геометрических фигур.Транзитивность – БО называют транзитивными если (А(ввер ногами)x,y,z)(хRу∩уRz)=˃хRz. Примеры: «больше», «меньше», «равно», «подобно», «выше», «севернее».

9. Дать определение бинарного отношения эквивалентности и класса эквивалентных элементов.

Бинарное отношение R на множестве А наз-ся отношением эквивалентности, если оно: 1.рефлексивно, т.е. ;2. симметрично, т.е R^-1=R; 3.транзитивно, т.е. RхR R(=R). Отношение эквивалентности обозначается . <x;y> .

Отношение эквивалентности явл. Обобщением отнош-я рав-ва. Ясно, что отношение равно на множ-ве действительных чисел явл-ся отношением эквивалентности. В самом деле, х=х; х=у => у=х; х=у =˃ y=z (для любых x,y,z ) .Если - отношение эквивалентности, то для любого х сечение называют классом эквивалентных элементов. Любые два элемента x,y (кл.эквив-ти) эквивалентны между собой. Любой элемент из них наз. представителем класса эквивал-х эл-тов. Теорема. Любые два класса эквивалентности либо совпадают, либо не пересекаются (не имеют общих элементов)

Док-во. Существует две возможности 1) . Во втором случае пусть

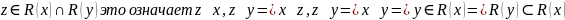
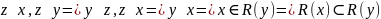Следовательно R(x)=R(y)

Следствие. Если R – отношение эквивалентности на множ-ве А, то А = , где R(x_i) – классы эквивалентности (пересекающиеся множества), а x₁ – представитель класса. При этом, если x_i Такое представление множ-ва А называется разбиением на классы эквивалентности. Опред-ие. Множество классов эквивалентности по отношению R называется фактор-множеством множ-ва А по отношению эквивалентности R. Таким образом, 1) каждое отношение эквивалентности R на А определяет разбиение множ-ва А на классы эквив-ти между собой эл-тов. 2) каждое разбиение множества А на пересекающиеся подмножества A_i определяет отношение эквивал-ти, при кот-м эквивалентными будут эл-ты A_i

10. Охарактеризовать отношение частичного порядка. Привести примеры частично упорядоченных и линейно упорядоченных множеств.

Отношение R AхА на множ-ве А называют 1) отношения строгого частичного порядка, если оно транзитивно R•R , асимметрично R^{-1 ,} антирефлексивно 2) отношения нестрогого частичного порядка, если оно транзитивно R•R , антисимметрично , рефлексивно Отношения строгого/нестрого порядка обозначаются также ) Множ-во, рассматриваемое вместе с отношением частичного порядка наз-ся упорядоченным множ-вом и обозначается

I) A=ℝ и R= - отношение строгого частичного порядка а) 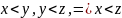б) в) <x;x>

II) A = ℝ и R= - нестрогое неравенство а)

III) A=p(U), R=⊂ - отношение нестрогого частичного порядка а) В⊂С, С⊂D=>B⊂D б) B⊂C, C⊂B=>B=C в) B⊂C

- Говорят, что два элемента x,y cравнимы между собой по отношению частичного порядка R, если xRy или yRx Говорят, что R является отношением линейного порядка , если любые два элемента x,z

Пример.

<ℝ,

<p(U), ⊂> не явл-ся линейно упорядоченным множеством.

11. Дать определение векторного (линейного) пространства над полем действительных чисел. Как выполняются действия над векторами арифметического пространства?

Множество V называется векторным пространством (над полем действительных чисел ℝ), если его элементы можно складывать между собой и умножать на действительные числа, причем эти действительные числа, причем эти операции обладают следующими свойствами (которые называются аксиомами векторного пространства) 1) сложение коммутативно: 2) сложение ассоциативно: 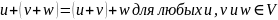3) в Vсуществует нулевой элемент 0 (или нуль): 4) для каждого существует противоположный ему элемент )= 5) умножение ассоциативно 6) умножение дистрибутивно относительно сложения: λ для любого числа λ 7) умножение на единицу тождественно: Элементы векторного пространства называются векторами

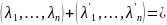
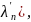
Пример1. Само множество ℝ действительных чисел является векторным пространством. Множ-во, состоящее из единственного эл-та – нуля, – также является векторным пространством. Оно обозначается 0 и называется тривиальным. Пример 2.Рассмотрим множество ℝⁿ = и положим Тогда ℝⁿ превращается в векторное пространство, которое называется n-мерным арифметическим пространством Пусть даны векторы Х и У 1)Суммой векторов Х и Y называется вектор Х+Y = (x₁+y₁,…x_n+y_n), т.е.при сложении векторов их соответствующие координаты складываются. 2) Произведением вектора Х= на число λ называется вектор λХ= , т.е. при умножении вектора на число каждая его из координат умножается на число 3)Скалярным произведением двух векторов X= и Y= называется число, равное сумме произведений соответствующих координат векторов Х*Y=x₁y₁+x₂y₂,…x_ny_n Св-ва ск.пр-ия 1)(X*Y)*Z=X*Z+Y*Z, (aX)*Y=a(X*Y), X*Y=Y*X 4)Два вектора называются ортогональными, если их скал.пр-ие рано 0 Лин.пр-во с введ-м ск-м в-ром наз-ся евклидовым n-мерным про-вом (мн-во 3мерн.в-ров R³,мн-во 2мерн.в-ров R²,мн-во R^-1=R-мн-во действ.ч.