Экзаменационая программа по курсу общей физики

(механика, основы термодинамики и молекулярной физики). ИТАЭ (ТЭ).

Лектор - Варава А.Н.

1. Материальная точка. Абсолютно твердое тело. Тело отсчета. Система отсчета. Кинематический закон движения материальной точки. Траектория. Вектор перемещения. Путь.

Материальной точкой называется физическое тело, размерами которого можно пренебречь

Абсолютно твердое тело – такое тело, которое не изменений свою формулу и размеры при любых скоростях движения.

Тело отсчета – это тело, относительно к-рого рассматривают положение других тел.

Система отсчета – система координат, связанная с телами отсчета плюс время.

Траектория – линия, которая описывает тело при своем движении в пространстве

Перемещение – направленный отрезок прямой (вектор), соединяющий начальное положение тела с конечным

Вектор перемещения (положение задается кончиком….)

проекции вектора на координатные оси

Путь – расстояние, отсчитанное вдоль траектории

Кинематический закон движения материальной точки: уравнение или систему уравнения, определяющего положение тела в любой момент времени относительно выбранной с. отсчета.

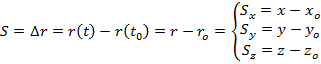
2. Скорость и ускорение Кинематический закон движения тела в случае постоянного ускорения. Скорость и ускорение при движении точки по криволинейной траектории. Нормальное и тангенциальное ускорение. Граница применимости классического способа описания движения точки.

Пусть за время точка совершает перемещение , описав при этом некоторую дугу l траектории, тогда можно ввести понятие средней скорости за время на перемещение . Разобьем дугу l на меньшие дугу , тогда для каждой дуги будем иметь свое и, следавательно свою среднюю скорость

Мгновенная скорость называется предел к при (произвольная )

Скорость характеризует перемещение в единицу времени

Ускорение характеризует изменение скорости за единицу времени.

Мгновенное ускорение определяется выражением:

Согласно определенно направлено по изменению скорости

Кинетический закон движения тела в случае постоянного ускорения

Начало условие: при t = 0,

Положение точки на окружности удобно характеризовать радиусом – вектор , проведенного из центра окружности. пусть за время dt точка совершила перемещение при этом радиус – вектор повернутые на угол . Таким образом при перемещении точки по окружности полоении вектора характуризует . Положение точки можем определить угом наклона радиус- вектора в выбранной оси OX. Угол назавем угловая координата. При этом примято считать вектор( аксиальной вектор). Напровление определяем по правилу правого винта. Если вращать рукоетку винта по напровленние движения точки, то поступательного движения винта – напровление точки

Угловая скорость согласно определить вектор направлена по ([] радиант)

[] c^-1

Углавая ускорение направлено по изменению угловой скорости

[] c^-2

Если имели равнопеременное движение точки по окружности, то кинематические законы движения для угловой координата и угловой скорости

Скорость

Ускорение

По касательной траектории в данной ее точке  a_ = Rsin90^o = R

называется касательноым ускорением, характеризующим изменение скорости по величине

По нормальной траектории в данной ее точке

называются тангенциальным ускорением, характеризующим изменение скорости по направлению

Тогда

Границы применимости классического способа описания движения точки:

Все вышеизложенное относится к классическому способу описания движения м. точки. В случае неклассического рассмотрения движения микрочастиц понятия траектории их движения не существует, но можно говорить о вероятности нахождения частицы в той или иной области пространства. Для микрочастицы нельзя одновременно указать точные значения координаты и скорости. В квантовой механике существует соотношение неопределенностей

В. Гайзенберга , где h=1,05∙10^-34 Дж∙с (постоянная Планка), которое определяет погрешности одновременного измерения координаты и импульса