Вопрос 28
29 Вопрос
Для
функции, зависящей от одной переменной
второй и третий дифференциалы выглядят
так:
Отсюда можно вывести общий вид дифференциала n-го порядка от функции :
При
вычислении дифференциалов высших
порядков очень важно, что
есть произвольное и не зависящее от
, которое при дифференцировании по
следует рассматривать как постоянный
множитель.
Дифференциалом
порядка n, где n > 1 от функции
в некоторой точке называется дифференциал
в этой точке от дифференциала порядка
(n — 1), то есть
Тейлора формула, формула.
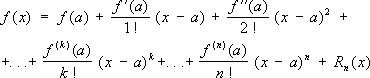
30 Вопрос
Опр.Функция F называеться первообразной функцией функции f на промежутке , если F диффиренцируема на в кааждой точке промежутка и вкаждой точке этого промежутка производна функци F равна значению функци f
F’(x)=f(x),x принодлежит промежутку
Две дифференцируемые на промежутке функции F и Ф являются первообразными одной и той же функции в том и только том случае , когда они отличаться на постоянную
Ф(х)=F(x)+c, х принадлежит промежутку С=const.
Опр. Пусть функция f определена на некотором промежутке , совокупность всех ее перообразных на это промежутке называется неопределённый интеграл от функции f и обозначается
f(x)
dx.
Если Функция F дифференцируема на некотором промежутке , то на нем dF=F(x)+C или что то же самое F’(x)dx=F(x)+c
Пусть функция f имеет первообразную на промежутке , для всех х принадлежащих этому промежутку имеет место равенство d f(x)dx=f(x)dx
Если функции f1 и f2 имеют первообразные на промежутке , то и функция f1+f2 имеют первообразные на этом промежутке , причем (f1(x)+f2(x))dx= f1(x)dx + f2(x)dx
Если функция f имеет первообразную на промежутке и к – число. То функция kf также имеет на том же промежутке первообразную ,причем к не=0 справедливо равенство
kf(x)dx=k f(x)dx
31 Вопрос
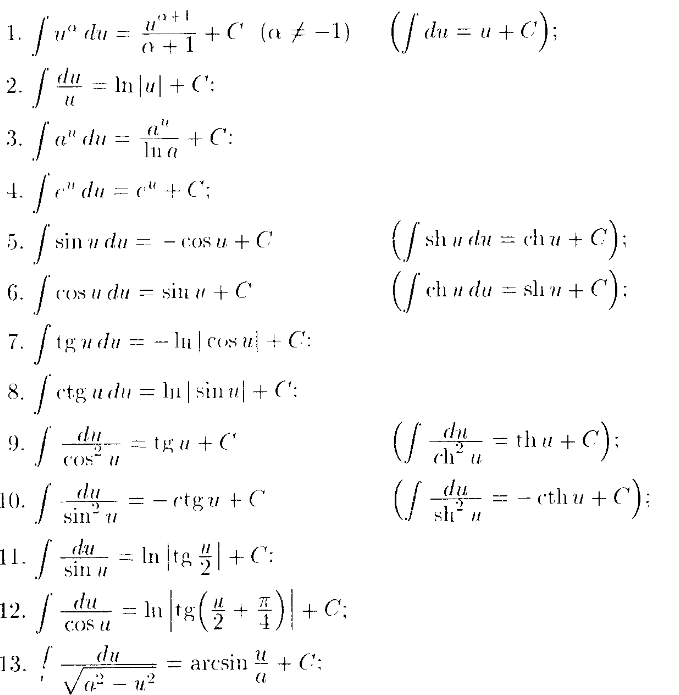
Если функция u(x) и v(x) дифференцируемы на некотором промежутке и на этом промежутки сущ. интеграл
vdu то на нем сущ. и интеграл udv причем
udv=uv- vdu.
32 Вопрос
Пусть
функция f
определена на , неотрицательна и
непрерывна на отрезке [a,b].
Тогда площадь S
множества G
={(x,y):a<x<b,0<y<f(x)}
выражается формулой S=
f(x)dx
.
Свойства
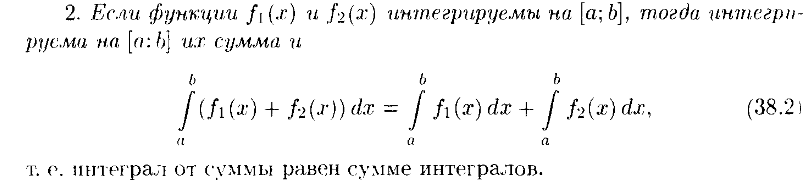
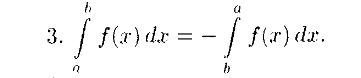
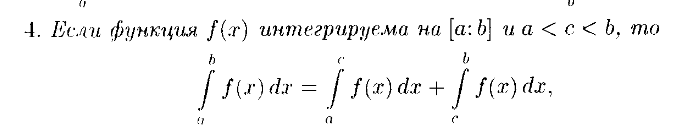
33 Вопрос
Пусть
функция f(x)
интегрируема на отрезке [a,b].
Тогда она интегрируема и на любом отрезке
[a,x]
, где a=<x=<b
т.е для любого х принадлежащего [a,b]
, имеет смысл интеграл
f(t)dt
.рассмотрим функцию F(x)=
f(t)dt
Эта функция F определена на отрезке [a,b] и называется интеграл с переменным верхним пределом.
Производная интеграла по верхнем пределу.
Если функция f интегрируема на отрезке [a,b] и не прерывна в точке х0 (х0 принадлежит [a,b]), то функция F(x)= f(t)dt дифференцируема в точке х0 и
F’(x0)=f(x0)
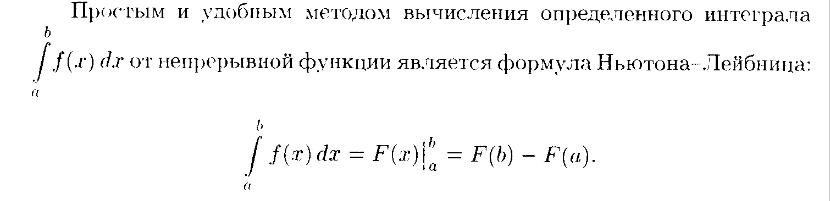
34 Вопрос
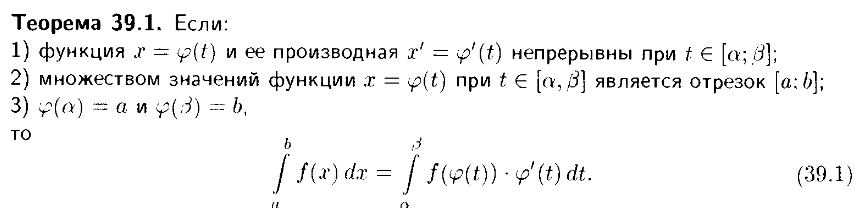
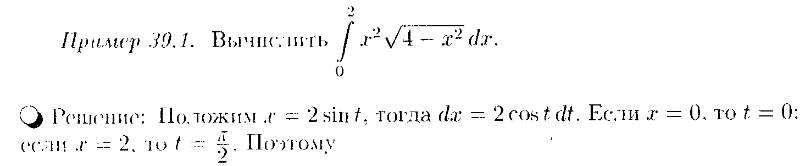
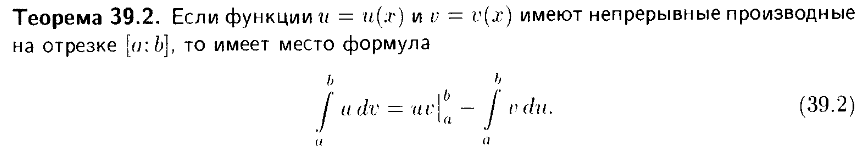
38 Вопрос
длина кривой,
заданной декартовым уравнением y
=
f(x),
,
определяется формулой
.
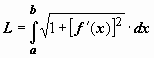Пусть
функция f
определена на , неотрицательна и
непрерывна на отрезке [a,b].
Тогда площадь S
множества G
={(x,y):a<x<b,0<y<f(x)}
выражается формулой S=
f(x)dx
.
39 Вопрос
Пусть функция f(x) неотрицательна и непрерывна на отрезке [a,b],а Q – тело полученное вращением криволинейной трапеции G , порождённая графиком функции f вокруг оси ох. Тогда для его объёма mesQ справедлива формула
MesQ= pi f**2(x)dx
Пусть Г = {r=r(t); a=<t=<b}-непрерывно диффернцируемая кривая без особых точек,лежащая вполуплоскасти y>0 плоскости переменых х,у. Тогда для площади L поверхности , полученой вращением кривой Г вокруг оси Ох ,справедлива формула
L=2*pi y*((xt’)**2+(yt’)**2)**1/2