Основные предпосылки создания: а) равновесное излучение(изл абс черного тела) б) непонятна линейчатость спектра в) необъяснимость фотоэффекта г) невозможность рассчитать теплоемкость твердых тел

Эргодическая гипотиза: среднее значение физической характеристики, которой обладает элемент статического ансамбля, совпадает со средним значением физ. Хар-ки, которой обладает элемент ансамбля, зависящего от времени.

постулаты Бора (1913г.): 1)Электрон движется по дискретным дозволенным орбитам, находясь на которых, он не излучает и не поглощает энергию, т.е. электрон имеет ряд дозволенных стационарных энергетических состояний.

2)При переходе из одного энергетического состояния в другое (с одной орбиты на другую) атом излучает или поглощает энергию.

Полуквантовое описание

Гипотеза Планка(1900г.): электрон в стенке полости, заполненной равновесным излучением, не может иметь произвольную энергию, пробегает ряд вполне определенных значений, кратных минимальному. n = 0,1,2,3 где ε – минимальное ненулевое значение энергии (квант Планка)

Принимая концепцию фотонов, приходим к естественному объяснению фотоэффекта: энергии фотона должно быть достаточно, чтобы совершить работу выхода и сообщить электрону некоторую кинетическую энергию

.

Принцип корпускулярно-волнового дуализма: и вещество, и поле представляю собой единую сущность. Проявление этого принципа осуществляется и зависит от условий эксперемента.

Де Бройль Движение частицы предлагается рассматривать как распространение некоторой волны, причем имеет место следующее соответствие:

Частица характеризуется	Сопоставляемая волна характеризуется
энергией ,	частотой ,
импульсом .	волновым вектором .

В простейшем случае свободного движения частицы естественно сопоставить единственно истинно свободную волну ― плоскую волну:

.

волновой пакет ― это суперпозиция плоских волн де Бройля, т.е. стационарных состояний.

Групповая скорость – скорость волнового пакета.

- равна скорости перемещения частицы.

1-ый постулат квантовой механики: Каждой квантовомеханической системе сопоставляется некоторая волновая функция(функция состояний) переменных конфигурационного пространства такая, что квадрат ее модуля пропорционален вероятности нахождения системы в единичном объеме в окрестности данной точки конфигурационного пространства.

Постулат был введен Максом Бором.

- 1-ый постулат.

Свойства: 1) ≠∞ ни в одной точке конфигурационного постранства. 2) ≠0 во всех точках конфигурационного пространства. 3) ооднозначна(не зависит из какой точки пришел наблюдатель). 4) непрерывна и число ее производных конечно. 5) Волновая функция определена с точностью до фазы.

Условие нормировки волновой функции в финитном пространстве:

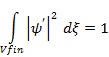, где

Условие нормировки волновой функции в инфинитном пространстве:

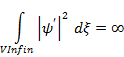- невозможно произвести нормировку.

2-ю аксиому квантовой механики ― принцип суперпозиции.

Если квантовомеханическая система может находиться в состоянии, описываемом волновой функцией , и может находиться в состоянии, описываемым волновой функцией , то для нее непременно реализуется состояние, представляющее суперпозицию этих функций: , где ― любые комплексные числа (в силу 1-й аксиомы не равные одновременно нулю).

Условие полноты: Любая функция, определенная в том же пространстве и с теми же условиями, не являющаяся функцией из набора Фурье, может быть представлена как суперпозиция функций Фурье:

, где а_k - весовые коэффициенты.

Среднее значение координаты :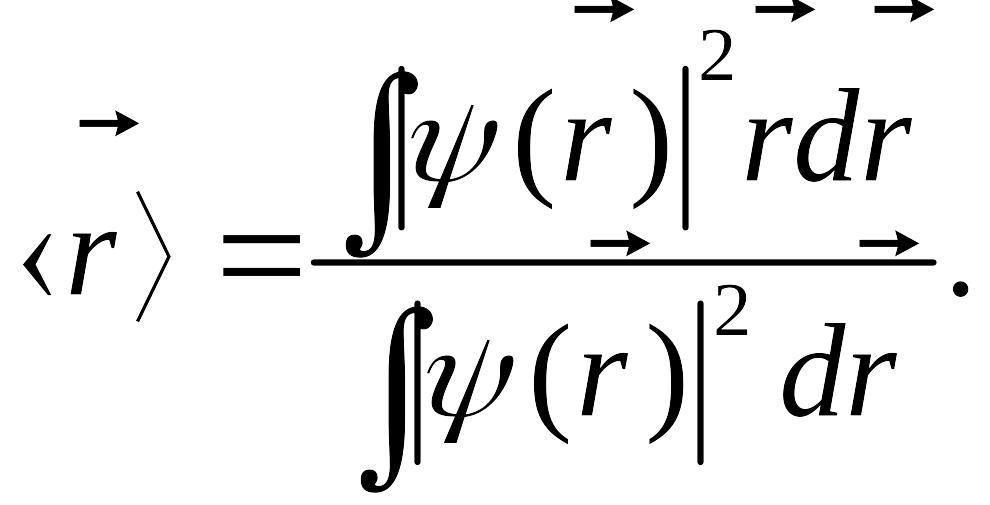 Интегрирование ведется по всему конфигурационному пространству, и в случае финитного движения интеграл в знаменателе равен единице, поэтому Среднее значение импульса: Также и для любой физической величины, зависящей от импульса, как нетрудно показать, имеет место формула

Аксиома о физическом операторе. Каждой физической величине в квантовой механике сопоставляется некоторый физический оператор , такой, что среднее значение физической величины вычисляется по формуле Интегрирование ведется по всему конфигурационному пространству.Чтобы не противоречить 2-ому постулату оператор должен быть линейным оператором.

Оператор называется транспонированным к оператору , если выполняетсяусловие:

.

Если эрмитовский оператор совпадает с сопряженным, то он является эрмитовски сопряженным. Любой оператор можно эрмитовски сопрячь. - эрмитовски сопряженный линейный оператор.

Если транспонирование и сопряжение опреатора совпадают, то он является эрмитовским.

Собственные функции и собственные значения операторов физических величин: по 3-му постулату средняя величина отклонения от среднего равна 0(ΔF = 0). ΔF = F - <F>; 𝛥 = - <F>.

Т.к. ΔF = 0, то F = <F>. Тогда ψ = <F>ψ, а значит ψ = Fψ – это уравнение на собственные функции и собственные значения оператора физ. величины.

Все собственные функции эрмитовского оператора физической величниы равны сопряженным самим себе функциям: F_n = F*_n.

Свойства собственных функций: 1) Дискретный спектр, отсутствует вырождение.

А) Собственные функции соответствующие различным собственным значениям ортогональны.

Тогда условие ортонормировки собственных функций оператора физической величины запишется: .

Б) Свойство полноты набора собственных функций физического оператора: Любую функцию, не принадлежащую набору собственных функций оператора физической величины и определенную в тех же граничных условиях, что и его собственные функции, можно представить в виде суперпозиции собственных функций с постоянными коэффициентами:

.