МАТЕМАТИЧЕСКАЯ ЛОГИКА
Высказывание – всякое связное, осмысленное повествовательное предложение, о котором вполне определенно можно сказать, истинно оно или ложно; ни одно высказывание не может быть одновременно истинным и ложным. Высказывания обозначаются большими и малыми буквами латинского алфавита.
Логические операции над высказываниями:
1)
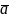– “не a”, отрицание
a |
|
1 |
0 |
0 |
1 |
2) a ʌ b – “a и b”, конъюнкция
a |
b |
a ʌ b |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
3) a v b – “a или b”, дизъюнкция
a |
b |
a v b |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
4) a → b – “из a следует b”, импликация; a – условие, посылка; b – следствие, заключение;
a |
b |
a → b |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
5) a ↔ b – “а эквивалентно b”, эквиваленция
a |
b |
a ↔ b |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
Высказывание, представляющее собой одно утверждение, называется простым (элементарным, пропозициональным).
Формулы алгебры высказываний – выражения, полученные из символов высказывательных переменных, знаком пяти операций (˥, ʌ, v, →,↔) и скобок, определяющих порядок действий.
1) пропозициональные переменные – формулы;
2) если x и y – формулы, то ¬x, x v y, x ʌ y, x → y, x ↔ y тоже формулы;
3) других высказываний нет.
Если формула для любых значений высказывательных переменных принимает значение истина, то она называется тождественно истинной. ТИ формула – тавтология.
Если формула для любых значений высказывательных переменных принимает значение ложь, то она называется тождественно ложной. ТЛ формула – противоречие.
Формулы, принимающие значение истина хотя бы для одного набора переменных называются выполнимыми.
A и B равносильны, если для любого x1, x2, … , xn, где это совокупность всех переменных, входящих в A и B, эти формулы принимают одинаковые значения.
Свойства равносильности: 1) рефлексивность A ~ A; 2) симметричность A ~ B <-> B ~ A; 3) транзитивность A ~ B ʌ B ~ C -> A ~ C.
Основные формулы эквивалентности:
1) ¬(¬X) = Y
2) X ʌ Y = Y ʌ X – коммутативность
3) X v Y = Y v X – коммутативность
4) X ʌ (Y ʌ Z) = (X ʌ Y) ʌ Z – ассоциативность
5) X v (Y v Z) = (X v Y) v Z – ассоциативность
6) X ʌ (Y v Z) = (X ʌ Y) v (X ʌ Z) – дистрибутивность
7) X v (Y ʌ Z) = (X v Y) ʌ (X v Z) – дистрибутивность
8) ¬(X ʌ Y) = ¬X v ¬Y – Де-Моргана
9) ¬(X v Y) = ¬X ʌ ¬Y – Де-Моргана
10) X v ¬X = 1
11) X ʌ ¬X = 0
12) X ʌ 1 = X
13) X v 1 = 1
14) X ʌ 0 = 0
15) X v 0 = X
16) X ʌ X = X – идемпотентность
17) X v X = X – идемпотентность
18) X ʌ (X v Y) = X – закон поглощения
19) X v (X ʌ Y) = X – закон поглощения
20) X -> Y = ¬X v Y
21) X -> Y = ¬Y -> ¬X
22) X <-> Y = (X -> Y) ʌ (Y -> X)
23) X <-> Y = (¬X v Y) ʌ (X v ¬Y)
Рассмотрим множество элементов любой природы M, в котором определены операции “+”, “×”, “˥”, “=” подчиняются следующим аксиомам:
1) x + y = y + x |
1) xy = yx |
2) x + (y + z) = (x + y) + z |
2) (xy)z = x(yz) |
3) |
3) |
4) x + yz = (x + y)(x + z) |
4) x(y + z) = xy + xz |
5) ¬(¬x) |
|
6) ¬(x + y) = ¬x¬y |
6) ¬(xy) |
7) x + xy = x |
7) x(x + y) = x |
Такое множество называется булевой алгеброй.
В тех случаях, когда для некоторой системы аксиом удается подобрать конкретные объекты и конкретные соотношения между ними так, что все конкретные аксиомы выполняются, то говорят, что найдена модель данной системы аксиом.
Формулы, в которые входят операции ʌ, v, ˥, причем ˥ относится лишь к высказывательным переменным, называются приведенными.
Назовем систему логических операций ∑ полной, если всякая формула эквивалентна некоторой формуле, в которую входят только операции из системы ∑.
Введем новые операции:
1) Стрелка Пирса A↓B
A |
B |
A↓B |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
2) Штрих Шеффера A|B
A |
B |
A|B |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
Закон двойственности
Эквивалентности 2 и 3, 4 и 5, 6 и 7, 8 и 9 таковы, что могут быть получены друг из друга заменой ʌ на v и наоборот. При этом справедлив общим закон двойственности, позволяющий с помощь описанного выше преобразования из любых 2-х эквивалентных формул, состоящих из высказывательных переменных, с помощью ʌ, v, ¬ получить формулы тоже эквивалентные.
Формула А* называется двойственной формуле А, если она получается из А заменой ʌ на v и v на ʌ.
Если формула A – тавтология, то A* - противоречие.
Функцией алгебры логики или функцией Буля f(x1, x2, … , xn) называется функция, принимающая значения 1 и 0, аргументы которых принимают значения 1 и 0.
Такая функция имеет тип {0; 1}n -> {0; 1}.
ТИ И ТЛ функции АЛ – постоянные функции, а 2 равносильные функции – одна и та же функция.
f(x1, … , xi-1, xi, xi+1, … , xn) существенно зависит от xi, если существует такой набор a1, … , ai – 1, ai, ai + 1, … , an из 0 и 1 таких, что f(a1, …, ai-1, a, ai+1, …, an) != f(a1, …, ai-1, 1, ai+1, …, an).
Переменные, от которых функция f существенно зависит, называются существенными, а остальные – фиктивными.
Пусть f и g – функции. f и g равны (f = g), если для любых значений аргументов функции f и g совпадают.
Каждой формуле A в алгебре высказываний можно сопоставить функцию фи(A) такую, что фи(А) = фи(B).