4.4.11. Сравнение бб и бм.

Теор. 4.4.11.1 (о связи ББ и БМ функций). Пусть функции F(x) и (x) связаны соотношением F(x)= . F(x) - ББ тогда и только тогда, когда (x) -БМ.

Док-во. Необходимость. Пусть F(x) - ББ, докажем, что - БМ. Возьмём . По определению ББ, для М=1/ : 0<| x-a |<| F(x) |> М. Тогда , т.е. (x) удовлетворяет определению БМ.

Достаточность доказывается аналогично необходимости.

5.1. Определение непрерывности функции в точке.

Опр.5.1.1. Пусть функция y = f(x) определена в точке х₀ и некоторой её окрестности. Функция f(x) называется непрерывной в точке х₀, если:

1.  2. .

опр.5.1.1 на язык -: Опр.5.1.2. Пусть функция y = f(x) определена в точке х₀ и некоторой её окрестности. Функция f(x) называется непрерывной в точке х₀, если для 0 существует положительное число , такое что для всех х из -окрестности точки х₀ (т.е. если х- х₀ ) выполняется неравенство  f(x) - f(х₀) .

Опр.5.1.3. Пусть функция y=f(x) определена в точке х₀ и некоторой её окрестности. Функция f(x) называется непрерывной в точке х₀, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

на языке последовательностей:Опр.5.1.4. Функция f(x) называется непрерывной в точке х₀, если для любой последовательности точек области определения, сходящейся к х₀, последовательность соответствующих значений функции сходится к f(х₀): .

Теор.5.2.1 о непрерывности суммы, произведения, частного. Пусть функции f(x), g(x) непрерывны в точке х₀. Тогда в этой точке непрерывны функции f(x)g(x), f(x)g(x), (частное - в случае, когда g(х₀)0).

Док-во непосредственно следует из теор.4.4.10 раздела 4.4.6 "Арифметические действия с пределами". Для примера докажем непрерывность частного. Пусть f(x), g(x) непрерывны в точке х₀, т.е. , , причём g(х₀)0. По теор.4.4.10 существует , и этот предел равен , что означает непрерывность функции в точке х₀

4.4.6. Арифметические действия с пределами.

Теорема 4.4.10. Пусть функции f(x), g(x) имеют предел при хa, С=const. Тогда имеют пределы функции С f(x), f(x)g(x), f(x)g(x), ( если ), и

4.4.10.1. ;

4.4.10.2. ;

4.4.10.3. ;

4.4.10.4. .

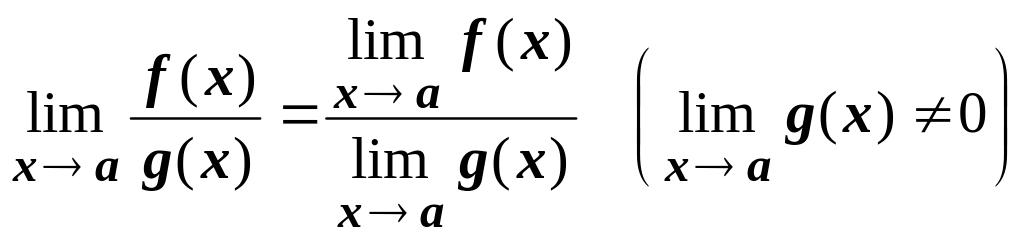Док-во основано на теор. 4.4.9 о связи функции с её пределом. Пусть ,  f(x)=b₁+(х), g(x)=b₂+(х), где (х), (х) - БМ. Тогда:

4.4.10.1. Сf(x)=Сb₁+С(х); С(х) - БМ по теор. 4.4.7 .

4.4.10.2. ; (х)(х) - БМ  .

4.4.10.3. . Выражение в квадратных скобках - БМ   .

4.4.10.4. Оценим : . В числителе стоит БМ, функция - ограничена при   .

4.3.3. Число е.

Утв. 1. Последовательность возрастает с ростом n.

Док-во. По формуле бинома Ньютона

Эта сумма содержит ровно n+1 член. Если перейти от n к n+1, то количество слагаемых увеличится на 1 и каждое слагаемое возрастёт a_n+1>a_n.

Утв. 2. Последовательность ограничена.

Док-во. Оценим величину сверху. Каждое слагаемое в полученной сумме оценивается величиной . Тогда вся сумма

Итак, последовательность возрастает и ограниченаона имеет предел.

4.4.7. Замечательные пределы.

4 .4.7.1. Первый замечательный предел. =1 Докажем, что sin| x |.| x | (достаточно доказать это при х>0). Рассмотрим круг радиуса 1 с центром в точке О. В качестве переменной х будем брать центральный угол, отсчитываемый в радианах от радиуса ОА. Тогда длина дуги АВ =х, длина отрезка ВD =sin х, sin х< х (при х 0; перпендикуляр - кратчайшее расстояние от точки до прямой). 2. Сравним площади треугольников OBА, OCA и сектора OBA: S(тр.OBА)<S(сек.OBA)<S(тр.OCA). Выразим эти площади: (CA=tg x). Делим это выражение на : . Мы получили эти неравенства в предположении х>0, но вследствие четности входящих в них выражений они верны при любом знаке х. 3. Переворачиваем эти неравенства: . cos x1 при х0, предел правой части тоже равен 1, по теор. 3.4.5 о пределе промежуточной функции  .

4.4.7.2. Второй замечательный предел. .

Распространим на случай действ переменной, докажем, что. Пусть n=E(x), тогда n x <n+1. Если x +, то и n, поэтому можем считать n >1. Из неравенства вследствие монотонного возрастания степенной функции с аргументом и степенью >1, получим . Предел правого члена при n равен числу е, предел левого тоже равен числу е. По теор. 4.4.6 о пределе промежуточной функции  , и он тоже равен числу е. Далее, , и снова применяя теор. 4.4.6 о пределе промежуточной функции, получаем, что существует и равен числу е.

Пусть теперь x -. Введём новую переменную y=-x-1,тогда x=-y-1, и y+ при x -. . Доказано, что односторонние пределы при x  существуют и равны(по теор. 4.4.1)  .

20