Односторонние пределы

Пусть функция f(x) определена на интервале (x₀, x₁).

Число A называется пределом функции f(x) справа, в точке x₀ если для любого ε > 0 найдется δ > 0 такое, что для всех x, для которых x₀ < x < x₀ + δ , справедливо неравенство | f(x) − A | < ε, т.е.

lim x → x0 + 0  f(x) = A       ε > 0     δ > 0 :     x0 < x < x0 + δ      | f(x) − A | < ε.

Предел функции f(x) в точке x₀ справа обозначается символом f(x₀ + 0)

Число A называется пределом функции f(x) слева, в точке x₁ если для любого ε > 0 найдется δ > 0 такое, что для всех x, для которых x₁ − δ < x < x₁ , справедливо неравенство | f(x) − A | < ε, т.е.

lim x → x1 − 0  f(x) = A       ε > 0     δ > 0 :     x1 − δ < x < x1      | f(x) − A | < ε.

Предел функции f(x) в точке x₁ слева обозначается символом f(x₁ − 0)

Теорема 4. Для того чтобы существовал предел 

lim

x → a

 f(x) , равный A, необходимо и достаточно, чтобы существовали и были равны A оба односторонних предела 

lim

x → a − 0

 f(x)  и 

lim

x → a + 0

 f(x) .

Функция f(x) называется ограниченной в точке x₀, если существуют число M > 0 и окрестность O(x₀), такие что    x  O(x₀)      | f(x) | < M .

Теорема 5. Если функция f(x) определена в некоторой окрестности точки x₀ и имеет в точке x₀ односторонние пределы, то она ограничена в этой точке.

Доказательство приведено в книге Я.С. Бугрова и С.М. Никольского “Дифференциальное и интегральное исчисление”. М.: ФИЗМАТЛИТ, 2002. Стр. 81.

Функция f(x) называется бесконечно большой при x → x₀, если

 M > 0      · O  (x0) :     x   · O  (x0)     | f(x) | > M.

В этом случае принято говорить, что предел функции бесконечен, и записывать этот факт в виде

 

lim x → x0  f(x) = ∞.

Прямая x = x₀ называется вертикальной асимптотой графика функции y = f(x), если хотя бы один из односторонних пределов f(x₀ + 0) и f( x₀ − 0) равен + ∞ или −∞.

таблица эквивалентности бесконечно малых

1.sinα(x)~α(x)

2.arcsinα(x)~α(x)

3.tgα(x)~α(x)

4.arctgα(x)~α(x)

5.loga(1+α(x))~(logae)α(x)

6.ln(1+α(x))~α(x)

7.a^α(x)-1~α(x)lna,a>0,a≠1

8.e^α(x)-1~α(x)

9.(1+α(x))^μ-1~μα(x)

10.корень n-ой степени из(1+α(x))-1~α(x)/n

11.корень кв.из(1+α(x))-1~α(x)/2

12.1-cosα(x)~1/2α^2(x)

Производной функции f(x) в точке х=х0 называется предел отношения функции в этой точке к приращению аргумента, если он существует.

1) Физический смысл производной. 

Если  функция y = f(x) и ее аргумент x являются физическими величинами,  то производная   – скорость изменения переменной y относительно переменной x в точке .  Например, если S = S(t) – расстояние, проходимое точкой за время t,  то ее производная – скорость в момент времени .  Если  q = q(t) – количество электричества, протекающее через поперечное сечение проводника в момент времени  t,  то   – скорость изменения количества электричества в момент времени , т.е. сила тока в момент времени .

2) Геометрический смысл производной.

Пусть – некоторая кривая, – точка на кривой .

Любая прямая, пересекающая не менее чем в двух точках называется секущей.

Касательной к кривой в точке называется предельное положение секущей  ,  если точка стремится к ,  двигаясь по кривой.

Из определения очевидно, что если касательная к кривой в точке существует, то она единственная

Рассмотрим кривую y = f(x)  (т.е. график функции  y = f(x)).  Пусть в точке он имеет невертикальную касательную .  Ее уравнение: (уравнение прямой, проходящей через точку и имеющую угловой коэффициент  k).

По определению углового коэффициента , где – угол наклона прямой   к оси .

Пусть – угол наклона секущей к оси ,  где  . Так как – касательная, то при

⇒ ⇒   .

Следовательно,

.

Таким образом, получили, что – угловой коэффициент касательной к графику функции y = f(x) в точке (геометрический смысл производной функции в точке).  Поэтому уравнение касательной к кривой y = f(x) в точке можно записать в виде

Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)): dy=ƒ'(х)•∆х.              

Геометрический смысл:дифференциал функции у=ƒ(х) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение ∆х.

Теорема Ферма.  Если функция у = f (х),  определенная в интервале (а ; b), достигает в  некоторой точке с этого интервала наибольшего (или наименьшего) значения и существует  производная f ′(с), то f ′(с) = 0.  

Геометрический смысл этой теоремы состоит в том, что касательная к графику функции у = f (х) в точке с абсциссой с параллельна оси абсцисс (рис.).    Теорема Ролля. Если функция у = f (х),  непрерывная на отрезке [а ; b] и  дифференцируемая в интервале (а ; b), принимает на концах этого отрезка равные значения f (a) = f (b), то в интервале (а ; b) существует такая точка с, что f ′(с) = 0.  Геометрически эта теорема означает  следующее: если крайние ординаты кривой у = f (х) равны, то на кривой найдется точка, в которой касательная параллельна оси абсцисс (рис.).    Теорема Лагранжа. Если функция у = f (х) непрерывна на отрезке [а ; b] и  дифференцируема в интервале (а ; b), то в этом интервале найдется такая точка с, что   

Эта теорема имеет простой геометрический смысл (рис.): на графике функции у = f (х)  между точками А и В найдется такая внутренняя точка С, что касательная к графику в точке Спараллельна хорде АВ.   

Следствие. Если f ′(x) = 0 в интервале (а ; b), то в этом интервале функция f (х) постоянна.  

Теорема Коши. Если функции f (х) и g (х): 1) непрерывны на отрезке [а ; b];  

2)  дифференцируемы в интервале (а ; b);  

3) g'(x) ≠ 0 в этом  интервале,  

то в интервале (а ; b) существует  такая точка с, что имеет место равенство 

 

Функция f(x) называется непрерывной на интервале (a, b), если она непрерывна в каждой точке этого интервала.

Функция f(x) называется непрерывной на отрезке [a, b], если она непрерывна на интервале (a, b), непрерывна справа в точке a и непрерывна слева в точке b.

Замечание. Функция, непрерывная на отрезке [a,b] может быть разрывной в точках a и b (рис. 1)

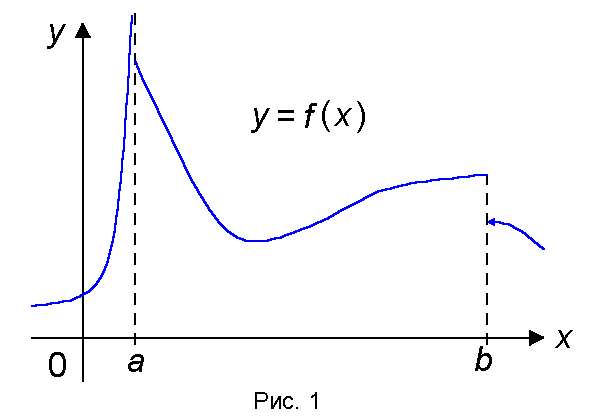
Множество функций, непрерывных на отрезке [a, b] обозначается символом C[a, b].