4. Типовые звенья и их передаточные функции. Интегрирующее звено. Ду, передаточная и переходная характеристики.

Дифференциальное уравнение интегрирующего звена имеет вид:

(2.10)

Коэффициент называется коэффициентом усиления интегрирующего звена. При нулевых начальных условиях (т.е если при имеем ) у интегрирующего звена выходная величина пропорциональна интегралу входной величины:

Записываем дифференциальное уравнение звена (2.10) в алгебраической операторной форме, получим: ,откуда находим передаточную функцию звена: (2.11)

Дифференциальное уравнение интегрирующего звена можно записать в другой форме: , где .

При этом передаточная функция звена примет вид: (2.12)

На рис. 2.4 представлен характер изменения выходной величины интегрирующего звена

из уравнения (2.11) получим как реакцию звена (цепи) на единичное входное воздействие, выраженную в алгебраической форме. Запишем данное равенство в форме оригинала функции, выполнив обратное преобразование Лапласа:

, (2.13)

если входное воздействие является единичным, т.е. соответствует , тогда преобразование можно записать: .Часто в качестве такого звена используется операционный усилитель в режиме интегрирования. Интегрирующим звеном является также обычный гидравлический демпфер или интегрирующий привод.

Интегрирующее звено с замедлением

Звено описывается дифференциальным уравнением (2.15)

Передаточная функция звена (2.16)

Примером такого звена является двигатель, если в качестве выходной величины рассматривать не угловую скорость, а угол поворота, являющийся интегралом от угловой скорости. Интегрирующее звено с замедлением можно представить как совокупность двух включенных последовательно звеньев – идеального интегрирующего и апериодическое первого порядка. Для нахождения временных характеристик удобно передаточную функцию представить в виде алгебраической суммы ,что позволяет представить решение дифференциального уравнения (2.20) в виде суммы решений для идеального интегрирующего звена и апериодического звена первого порядка.

(2.17)

А симптотическая ЛАХ представляет собой две прямые с отрицательными наклонами -20 дБ/дек (при ) и -40 дБ/дек (при ).

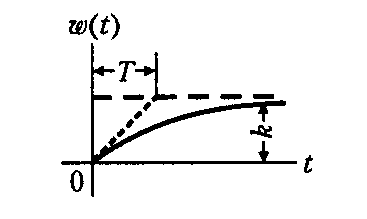
Изодромное звено

Звено записывается уравнением (2.18)

Передаточная функция звена ,

г де – постоянная времени изодромного звена. Звено можно представить в виде совокупности двух звеньев, действующих параллельно, идеального интегрирующего с коэффициентом передачи и безынерционного с коэффициентом передачи .Таким звеном может быть комбинация пружины с демпфером. Логарифмическая амплитудно-частотная характеристика (ЛАХ) строится по выражнию: .

5. Типовые звенья и их передаточные функции. Инерционное звено первого порядка, ду, передаточная и переходная характеристики. Пример реализации.

Инерционному звену первого порядка соответствует дифференциальное уравнение (2.25)

В операторной форме: .

Передаточная функция инерционного звена первого порядка . (2.26)

Дифференциальное уравнение достаточно просто решается обычным методом.

По таблицам преобразования Лапласа находим изображение входной величины:

.

Изображение выходной величины равно: ,

Выражаем оригинал функции через ее изображение (производим обратное преобразование), вынося постоянную величину за знак преобразования Лапласа:

.

Полагая , по таблицам преобразования Лапласа находим:

. (2.27)

Переходный процесс инерционного звена первого порядка представлен на рис.

К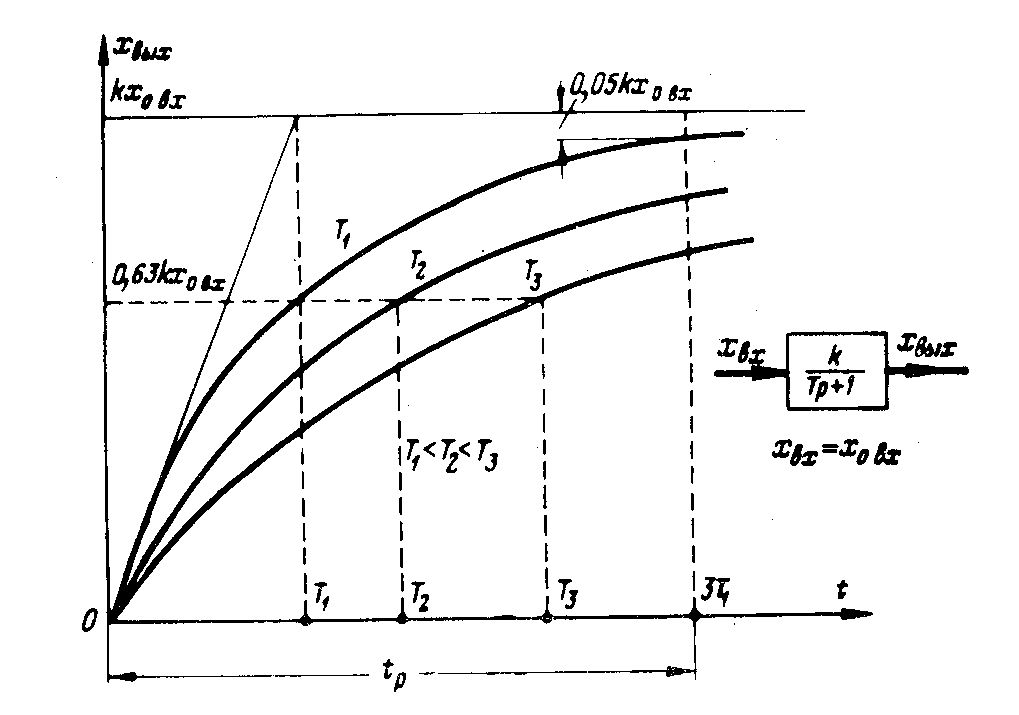 ривые переходных процессов имеют вид экспонент

В качестве первого примера можно рассмотреть двигатель любого типа (электрический, гидравлический, пневматический и т.д.), На рис. 2.11 приведены примеры реализации инерционных звеньев первого порядка как пассивных электрических цепей.

Входной величиной этих звеньев является напряжение , а выходной – напряжение .

Согласно второму закону Кирхгофа для электрической цепи (рис. 2.11, а) можно записать:

,

откуда .

По первому закону Кирхгофа .

Подставив значение в выражение для , получим: .

Преобразовав дифференциальное уравнение по Лапласу, получим следующую алгебраическую форму: ,

откуда находим передаточную функцию звена ,

где .

Таким образом, электрическая цепь, изображенная на рис. 2.11, а, является инерционным звеном первого порядка (апериодическим звеном).

Коэффициент передачи звена регулируется величинами сопротивлений и , при этом пропорционально коэффициенту передачи изменяется и постоянная времени.

При получаем электрическую цепь (рис. 2.11, б), коэффициент передачи, постоянная времени и передаточная функция которой в этом случае будут равны: .Электрическая цепь, представленная на рис. 2.11, б, является апериодическим звеном с коэффициентом передачи, равным единице.