Лекция № 1 Преобразование Лапласа

Учебная цель: дать понятие об общих принципах операционного исчисления, формировать знания о преобразовании Лапласа функций ограниченного роста, об обратном преобразовании Лапласа, об оригинале и изображении.

Учебные вопросы:

1. Преобразование Лапласа функций ограниченного роста.

2. Простейшие свойства преобразования Лапласа.

3. Теоремы подобия, смещения, запаздывания.

Литература:

1. Пискунов Н.С. Дифференциальное и интегральное исчисления для ВТУЗов. Т.2, гл.19.

Введение

Операционное исчисление (ОИ) – одна из важнейших областей математического анализа. Методы ОИ используются в физике, механике, электротехнике и других науках при решении различных вопросов. Особенно широкое применение ОИ имеет в автоматике и телемеханике.

Еще в 19 веке математики начали заниматься так называемым символическим исчислением, в котором проводятся формальные операции над величиной р, которая является символом дифференцирования, например, если есть функция , то умножение означает дифференцирование функции :

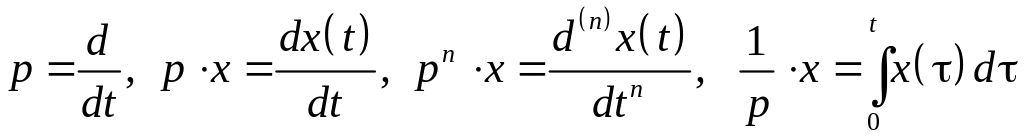
Популяризации символического исчисления в значительной степени способствовал английский инженер Хевисайд, который успешно применял его в решении дифференциальных уравнений, связанных с различными электрическими процессами. Однако он не заботился о строгом математическом обосновании метода, что иногда приводило к неверным результатам.

Строгое математическое обоснование метода появилось лишь в 20-е годы 20 века. В основе его лежит так называемое преобразование Лапласа. Суть этого метода заключается в следующем. Операции дифференцирования и интегрирования заменяются некоторыми алгебраическими операциями. В результате дифференциальное уравнение заменяется алгебраическим. Находится алгебраическое решение, а по нему восстанавливается искомое решение дифференциального уравнения.

Вопрос 1. Преобразование Лапласа функций ограниченного роста.

Определение 1. Комплекснозначная функция вещественного аргумента t называется функцией ограниченного роста с показателем , если она по модулю возрастает не быстрее некоторой показательной функции, т.е.

1. существует такое число М (зависящее от функции f), что , ;

2. ;

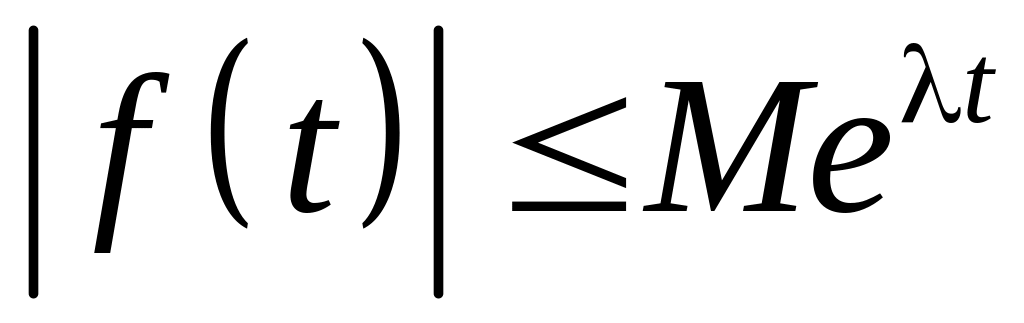3. функция кусочно-непрерывно дифференцируема на всей числовой оси и на каждом конечном промежутке она имеет конечное число точек разрыва 1-го рода.

График такой функции может выглядеть, например, так:

у

М

0 t

– М

Поскольку функции ограниченного роста при заведомо принимают нулевые значения, в дальнейшем мы будем задавать их аналитические выражения только при , не оговаривая это специально.

Например, вместо полного определения функции 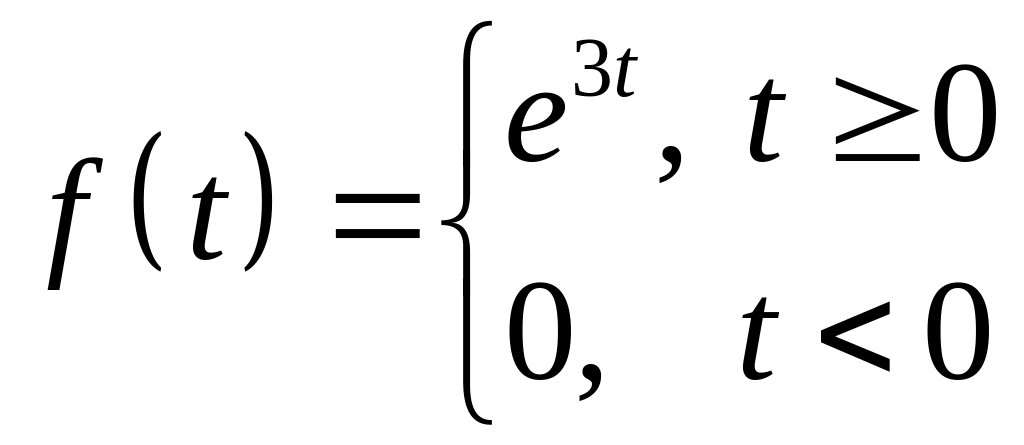будем использовать краткую запись , позволяющую утверждать, что – функция ограниченного роста с показателем .

Другой пример: .

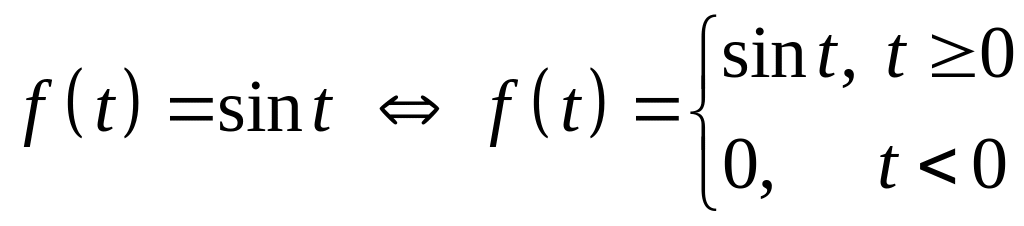Определение 2. Множество всех функций ограниченного роста с показателем  называется пространством функций ограниченного роста с показателем  и обозначается .

Хотя пространства включают в себя наиболее употребительные типы функций, многие функции не входят ни в одно из этих пространств.

Например, функция не является функцией ограниченного роста, поскольку при любых  и

.

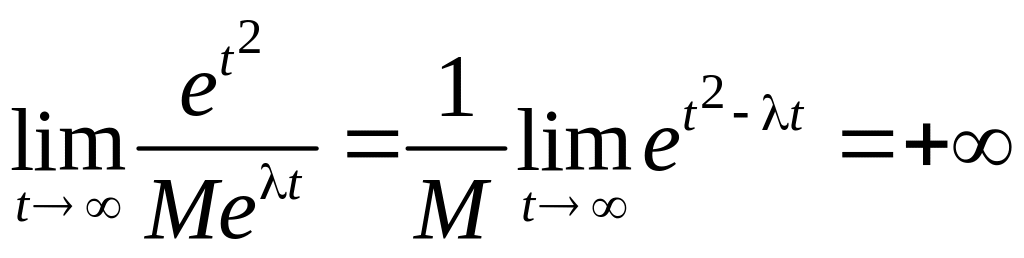Функция , где , также не принадлежит , ввиду имеющегося разрыва 2-го рода в точке .

Т еорема 1. Если функция , то зависящий от комплексного параметра р несобственный интеграл 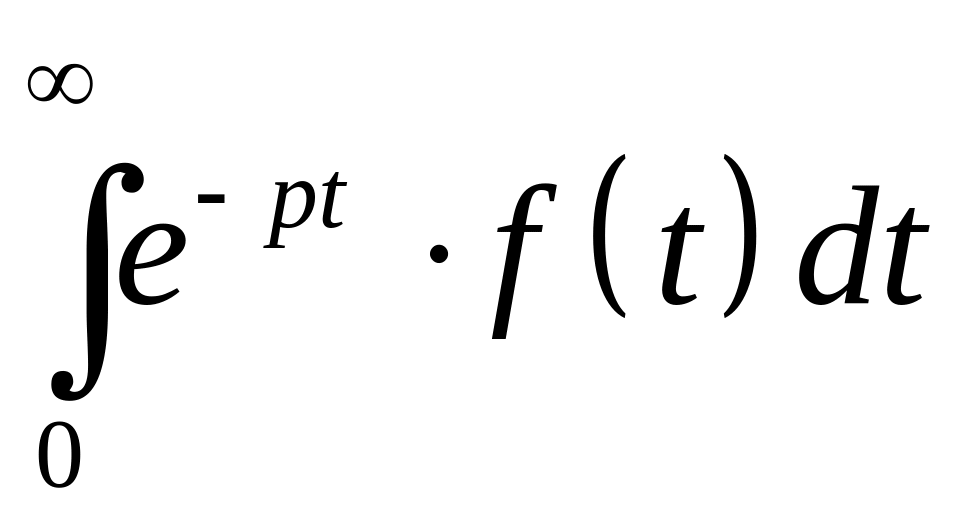абсолютно сходится при всех р, удовлетворяющих условию .

Доказательство.

Пусть р – комплексное число, .

Оценим величину :

, ,

,

(по определению 1), .

Итак, .

По условию , тогда .

Вычислим несобственный интеграл

,

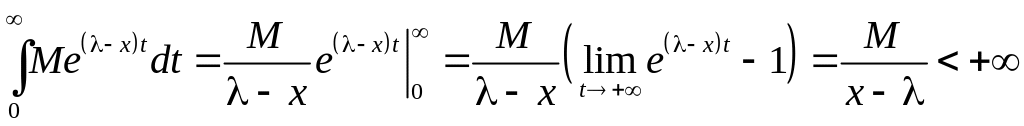т.е. интеграл сходится.

По признаку сравнения для несобственных интегралов от положительных функций из сходимости интеграла от большей функции следует сходимость интеграла от меньшей функции, следовательно, сходится интеграл , а значит, исходный интеграл сходится абсолютно.

Определение 3 (определение преобразования Лапласа). Пусть – пространство функций ограниченного роста с показателем , функция ; домножим ее на , где р – некоторое комплексное число и проинтегрируем по t от 0 до :

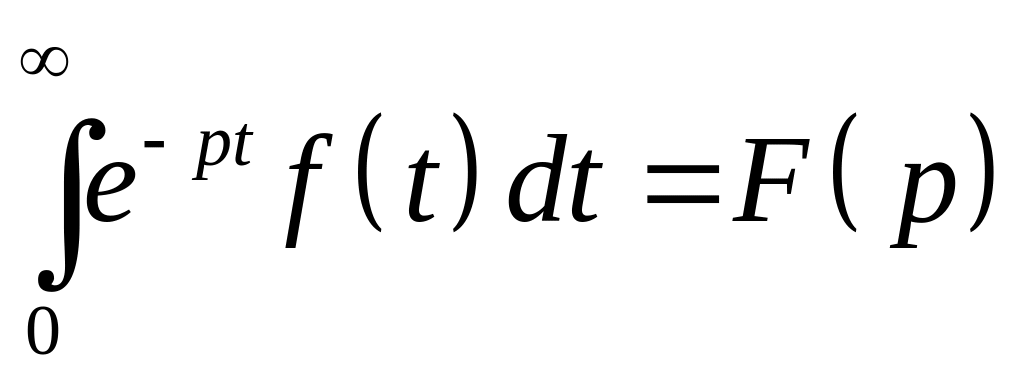. ( 1 )

Функция называется преобразованием Лапласа функции .

Функция (удовлетворяющая условиям 1) – 3)) называется оригиналом (прообразом), а функция – изображением Лапласа функции (или, короче, изображение, образ).

Обозначения:

или