Билет №35(Центробежные силы инерции, зависимость ускорения свободного падения от широты местности)

Рассмотрим диск, вращающийся вокруг перпендикулярной к нему вертикальной оси z’ с угловой скоростью w. Вместе с диском вращается надетый на спицу шарик, соединенный с центром диска пружиной. Шарик занимает на спице такое положение, при котором сила натяжения пружины F_пр оказывается равной произведению массы шарика m на его ускорение w_n=-w²R; R – радиус-вектор, проведенный к шарику из центра диска (R – расстояние шарика от центра диска): F_пр = -mw²R. Относительно системы отсчета, связанной с диском, шарик покоится. Это можно формально объяснить тем, что, кроме силы F_пр, на шарик действует сила инерции F_цб = mw²R, направленная вдоль радиуса от центра диска. Силу инерции F_цб, возникающую во вращающейся (по отношению к ИСО) системе отсчета, называют центробежной силой инерции. Эта сила действует на тело во вращающейся системе отсчета, независимо от того, покоится тело в этой системе или движется относительно нее со скоростью v’.

Вопрос №36 (Законы динамики твердого тела)

Уравнение движения центра масс. dP/dt=mdVc/dt=mWc=F_внешн. P=MiVi. Уравнение моментов:dMo/dt=N_oвнешн. Mo=[r,M_iV_i]; P=M_iV_i; dMc/dt=N_cвнешн. Условие равновесия твёрдого тела.Vx=0,P=0,Mo=0,F_i=0, F_xi=0; F_yi=0; F_zi=0; Ni=0; N_xi=0; N_yi=0; N_zi=0.Момент импульса твёрдого тела относительно оси вращения.r_i=R_ie_ri+z_ie_r; Vi=Ri[,e_ri]=[,R_i]=_zR_ie_; M_z=RiPi=zMiRiRi; Момент инерции: Iz=MiRiRi; M_z+I_z_z.

Вопрос №37 (Условия равновесия т.т.)

Условия равновесия т.т. (т.е. ). . Причём, относительно любой точки, т.к. все силы можно представить как совокупность пар сил (из условие, что сумма всех сил равна 0).

Вопрос №38 (Уравнение динамики для тела, вращ вокруг неподв оси)

о движения твёрдого тела вокруг неподвижной оси. dMz/dt=N_zвнешн; M_z=I_z_z; _z=d/dt; _z=d_z/dt; dM_z/dt=I_zd_z/dt=I_z_z=I_z^**(2-ая производная)=N_zвнешн; ₀(0)=_­0; _z(0)=_z0.

Вопрос №39( Момент импульса т.т. относительно оси вращения)

, где - расстояние частицы от оси вращения.

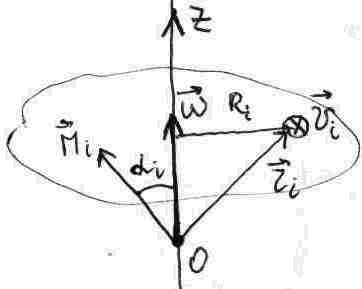
Вопрос №40.(Момент инерции. Теорема Штейнера)

I=M_ir²_i=R²dM=rdv; =dMdv, =dm/dV.Характеризует:1) Инертные свойства при вращательном движении(играет роль массы).2) Аддитивность. R=R_ic+a; I=M_iR²=MR²i+2amiR_ic+ma²; Теорема Штейнера: I=Ic+ma². Примеры:1)Стержень (через конец стержня) I₀=₀^xx²mdx/l=ml³/3; (через центр масс) Ic=I₀-m(l/2)²=ml²/12; 2) Сфера Ix=Iy=Iz=2mr²/3; 3) Однородный шар I=2r²4r²dr, =3m/4r³, I=2mr²/5; 4)Полу шар I=(1/2)(2/5)2mr²=2mr²/5; 5) Обруч Iz=Mir²=mr² ,Ix=Iy=Iz/2=Mr²/2; 6)Диск Iz=r²(m/r²)2rdr, Iz=mr²/2, Ix=Iy=mr²/4

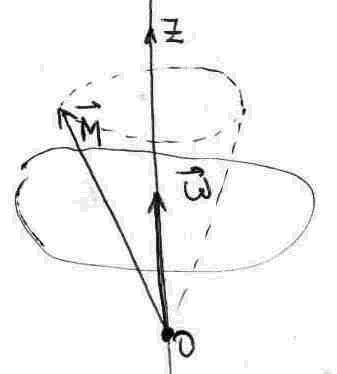
Вопрос №41 (Момент импульса т.т. относительно оси вращения.)

; ;В общем случае вектор момента импульса не совпадает по направлению с осью вращения тела z и поворачивается вместе с телом вокруг этой оси, описывая конус.

Вопрос №42(Кинет энергия вращ вокруг неподв оси тела)

; Если x,y,z – главные оси инерции, то

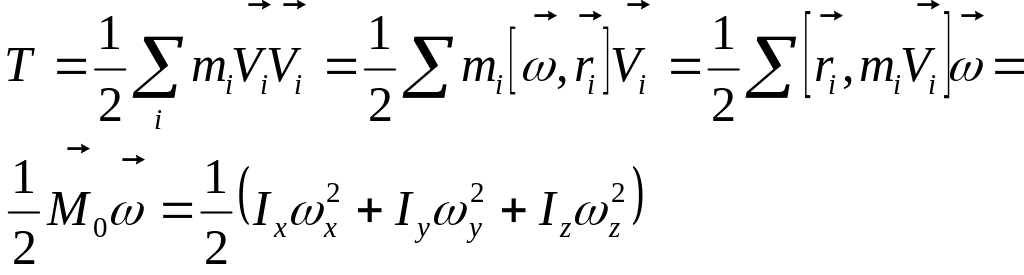
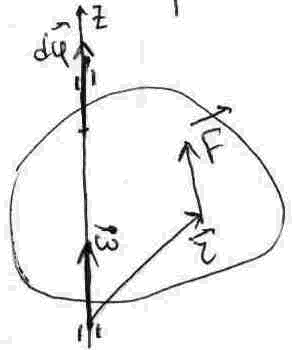
Вопрос №43 (Работа,внешними силами, вокруг неподвижноыыый оси)

;

Вопрос №44 (Уравнение динамики для плоского тела движения т.т)

Плоское движение т.т. – движение, при котором все точки т.т. движутся в параллельных плоскостях. (т.е. существует бесчисленное кол-во возможностей разложения) ; ;

Вопрос №45 (Кинетическая энергия т.т. при плоском движении)

, где -расстояние от частицы массы до оси вращения. Если в качестве точки О взять центр масс тела C, то , будет равен 0. И кинетическую энергию можно представить в виде: . Таким образом, кин. эн. тела при плоском движении слагается из энергии поступательного движения со скоростью, равной скорости

Вопрос №47 (Прецессия гироскопа)

Прецессия гироскопа – явление вращения гироскопа вокруг вертикали под действием силы тяжести.

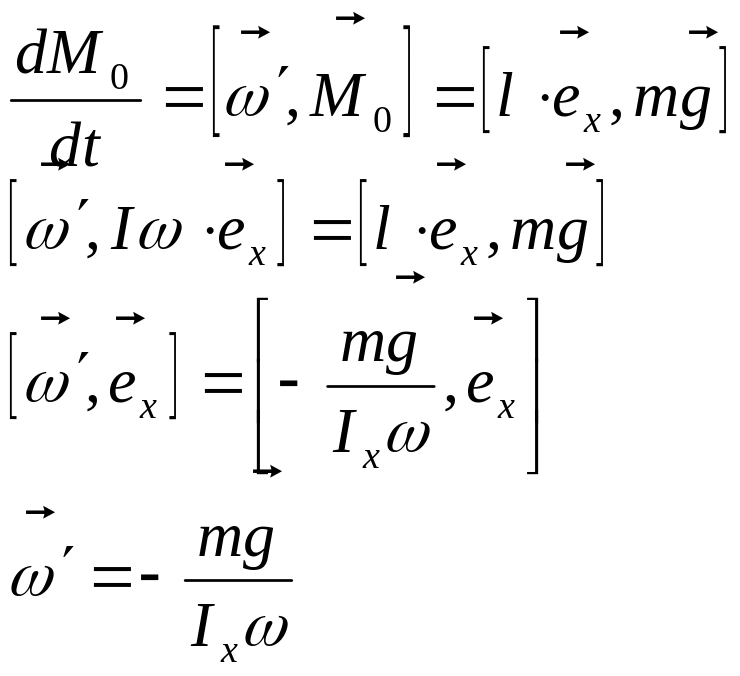
Выводы: 1.Направление ; 2. пропорциональна .