Геометрическая интерпретация — вариант 1

Рассмотрим формулу (2) — второй шаг алгоритма. Её геометрическое представление изображено на рис. 1:

1 — получение проекции вектора на ;

2 — вычисление , то есть перпендикуляра, которым выполняется проецирование конца на . Этот перпендикуляр — вычисляемый в формуле (2) вектор ;

3 — перемещение полученного на шаге 2 вектора в начало координат. Это перемещение сделано на рисунке лишь для наглядности. Оно не является математическим действием и поэтому не отражается в формуле (2).

На рисунке видно, что вектор ортогонален вектору , так как является перпендикуляром, по которому проецируется на .

Рассмотрим формулу (3) — третий шаг алгоритма — в следующем варианте:

Её геометрическое представление изображено на рис. 2:

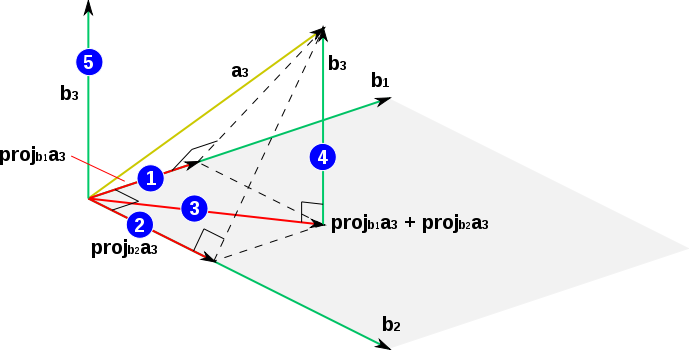
1 — получение проекции вектора на ;

2 — получение проекции вектора на ;

3 — вычисление суммы , то есть проекции вектора на плоскость, образуемую векторами и . Эта плоскость закрашена на рисунке серым цветом;

4 — вычисление , то есть перпендикуляра, которым выполняется проецирование конца на плоскость, образуемую векторами и . Этот перпендикуляр — вычисляемый в формуле (6) вектор ;

5 — перемещение полученного в начало координат. Это перемещение сделано на рисунке лишь для наглядности. Оно не является математическим действием и поэтому не отражается в формуле (6).

На рисунке видно, что вектор ортогонален векторам и , так как является перпендикуляром, по которому проецируется на плоскость, образуемую векторами и .

Таким образом, в процессе Грама — Шмидта для вычисления выполняется проецирование ортогонально на гиперплоскость, формируемую векторами . Вектор затем вычисляется как разность между и его проекцией. То есть — это перпендикуляр от конца к гиперплоскости, формируемой векторами . Поэтому ортогонален векторам, образующим эту гиперплоскость.

Геометрическая интерпретация — вариант 2

Рассмотрим проекции некоторого вектора на вектора и как компоненты вектора в направлениях и (рис. 3)

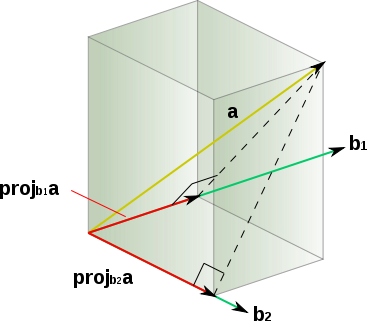
Если удалить из компоненту в направлении , то станет ортогонален (рис. 4):

Если из удалить компоненты в направлениях и , то станет ортогонален и , и (рис. 5):

В формуле (2) из вектора удаляется компонента в направлении вектора . Получаемый вектор не содержит компоненту в направлении и поэтому ортогонален вектору .

В формуле (3) из вектора удаляются компоненты в направлениях и (формуле 3 соответствует переход от рис. 3 к рис. 5; рис. 4 не соответствует формуле 3). Получаемый вектор ортогонален векторам и .

В формуле (4) из вектора удаляются компоненты в направлениях . Получаемый вектор ортогонален векторам .

Таким образом, по формулам (1) — (4) на основе векторов получается набор ортогональных векторов .

Численная неустойчивость

При вычислении на ЭВМ по формулам (1) — (5) вектора часто не точно ортогональны из-за ошибок округления. Из-за потери ортогональности в процессе вычислений классический процесс Грама — Шмидта называют численно неустойчивым.

Модифицированный процесс Грама — Шмидта

Процесс Грама — Шмидта может быть сделан более вычислительно устойчивым путём небольшой модификации. Вместо вычисления как

этот вектор вычисляется следующим образом:

Геометрическая интерпретация

Рассмотрим получение по формулам (8) — (11):

Геометрически это показано на рис 6:

На рис. 6 вектор обозначен как .

1 — получение проекции вектора на для формулы (12), то есть компоненты в направлении ;

2 — вычитание по формуле (12), то есть удаление из компоненты в направлении . Получаемый вектор ортогонален , так как не имеет компоненты в направлении ;

3 — перенос вектора в начало координат. Это перемещение сделано на рисунке лишь для наглядности. Оно не является математическим действием и поэтому не отражается в формуле (12).

4 — получение проекции вектора на для формулы (13), то есть компоненты в направлении ;

5 — вычитание по формуле (13), то есть удаление из компоненты в направлении . Получаемый вектор ортогонален , так как не имеет компоненты в направлении . При вычитании из компоненты в направлении в результирующем векторе не появляется компонента в направлении ;

6 — перенос вектора в начало координат. Это перемещение сделано на рисунке лишь для наглядности. Оно не является математическим действием и поэтому не отражается в формуле (13).

Таким образом, получаемый на рис. 6 вектор не имеет компонент в направлениях и и поэтому ортогонален и .

Рассмотрим непосредственно формулы (8) — (11).

В формуле (8) из вектора удаляется компонента в направлении вектора . Получаемый вектор не содержит компоненту в направлении и поэтому ортогонален вектору .

Далее в формуле (9) из результата удаляется его компонента в направлении вектора . Получаемый вектор не содержит компоненту в направлении и поэтому ортогонален вектору .

Путём дальнейшего последовательного удаления из результата его компонент получается вектор , не содержащий компонент в направлениях и потому ортогональный векторам .