Ортогональные векторы. Ортонормированный базис.

Определение. Два вектора называются ортогональными, если угол между ними равен прямому углу, т.е.

Обозначение: – векторы и ортогональны.

Определение. Тройка векторов называется ортогональной, если эти векторы попарно ортогональны друг другу, т.е. , .

Определение. Тройка векторов называется ортонормированной, если она ортогональная и длины всех векторов равны единице: .

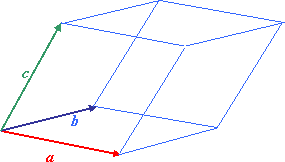
Замечание. Из определения следует, что ортогональная и, следовательно, ортонормированная тройка векторов является некомпланарной.

Три вектора называются некомпланарными, если концы равных им векторов, отложенных от одной точки, не лежат в одной плоскости с их общим началом.

Векторы являются компланарными, если их смешанное произведение равно нулю.

Векторы являются некомпланарными, если их смешанное произведение не равно нулю.

Смешанное произведение векторов равно определителю, составленному из координат этих векторов.

Найдём смешанное произведение векторов.

Следовательно, векторы некомпланарные.

Ортогональной проекцией вектора на ось, задаваемую вектором , называется его проекция на ось вдоль прямой (или вдоль плоскости), перпендикулярной данной оси. Ортогональную проекцию вектора на ось, задаваемую вектором , будем обозначать .

Ортогональную проекцию вектора на прямую будем обозначать .

Ортогональную проекцию вектора на плоскость будем обозначать .

Разность между вектором и его ортогональной проекцией называют ортогональной составляющей:

— — ортогональная составляющая вектора относительно вектора ;

— — ортогональная составляющая вектора относительно прямой ;

— — ортогональная составляющая вектора относительно плоскости .

На рис. 1.23 изображены ортогональные проекции вектора :

— на прямую (или на ось , задаваемую вектором ) вдоль прямой (рис.1.23,а);

— на прямую (или на ось , задаваемую вектором ) вдоль плоскости (рис.1.23,б);

— на плоскость вдоль прямой (рис.1.23,в).

На рис. 1.23 изображены ортогональные составляющие вектора :

— относительно оси (вектора ): (рис.1.23,а);

— относительно плоскости (рис.1.23,в).

Ортогонализация

Ортогонализация ― алгоритм построения для данной линейно независимой системы векторов евклидова или эрмитова пространства V ортогональной системы ненулевых векторов, порождающих то же самое подпространство в V.

Наиболее известным является процесс Грама ― Шмидта, при котором по линейно независимой системе строится ортогональная система такая, что каждый вектор b_i линейно выражается через , то есть матрица перехода от {ai} к {bi} ― верхнетреугольная матрица.

Алгоритм ортогонализации Грама - Шмидта

Процесс Грама ― Шмидта ― наиболее известный алгоритм ортогонализации, при котором по линейно независимой системе a₁,a₂,...,a_k строится ортогональная система b₁,b₂,...,b_k такая, что каждый вектор b_i линейно выражается через a₁,a₂,...,a_i, то есть матрица перехода от {a_i} к {b_i} ― верхнетреугольная матрица.

Этот процесс применим также и к счётной системе векторов.

(Процесс Грама ― Шмидта может быть истолкован как разложение невырожденной квадратной матрицы в произведение ортогональной (или унитарной матрицы в случае эрмитова пространства) и верхнетреугольной матрицы с положительными диагональными элементами, что есть частный случай разложения Ивасавы. )

Классический процесс Грама — Шмидта

Алгоритм

Пусть имеются линейно независимые векторы

Определим оператор проекции следующим образом:

где — скалярное произведение векторов и . Этот оператор проецирует вектор ортогонально на вектор .

Классический процесс Грама — Шмидта выполняется следующим образом:

На основе каждого вектора может быть получен нормированный вектор: (у нормированного вектора направление будет таким же, как у исходного, а длина — единичной).

Результаты процесса Грама — Шмидта:

— система ортогональных векторов либо

— система ортонормированных векторов.

Вычисление носит название ортогонализации Грама — Шмидта, а — ортонормализации Грама — Шмидта.