Департамент по авиации

Министерства траспорта и коммуникаций Республики Беларусь

Минский государственный высший авиационный колледж

Кафедра естественнонаучных дисциплин

КУРСОВАЯ РАБОТА (ПРОЕКТ)

Тема: Расчет частотных и фазовых характеристик четырехполюсника

По дисциплине: «Высшая математика»

Специальность: «Техническая эксплуатация радиоэлектронного оборудования»

Андрикевича Игоря Викторовича

Курса 2 группы Р110

Руководитель Степа Наталья Николаевна

Консультант Балодис Александра Ивановна

Курсант Андрикевич Игорь Викторович

Минск – 2011 г.

Департамент по авиации

Министерства транспорта и коммуникаций Республики Беларусь

Минский государственный высший авиационный колледж

УТВЕРЖДАЮ

Заведующий кафедрой ЕНД

__________Кириленко А.И.

«____»_____________20__г.

ЗАДАНИЕ

на курсовую работу (проект)

по дисциплине______________________________________________________

курсанта______________________курса__________________________группы

ф амилия имя отчество

Тема курсовой работы (проекта)_______________________________________

При выполнении курсовой работы (проекта) по данной теме должны быть представлены:

1.Пояснительная записка

2.Расчетно-графическая часть

3.Выводы

4.Список использованных источников

Руководитель

Курсовой работы (проекта) _________ _______________________________

подпись фамилия, имя, отчество

Консультант ____________________ _______________________________

подпись фамилия, имя, отчество

Дата выдачи _____ ________________20__г.

Срок сдачи ______ ________________20__г. Подпись курсанта____________

Минск – 2011г.

Оглавление:

Введение…………………………………………………………………4

1. Понятие добротности………………………………………………...4

2. Нахождение добротности осциллятора..……………………………8

3.Экспериментальная работа с наклонным маятником………………9

3.1.Порядок выполнения эксперемента……………………………...9

3.2.Обработка результатов измерения……………………………….9

3.3.Опесание установки…………………………………………...….10

3.4.Результаты эксперемента………………………………………...11

4. Затухающие колебания………………………………………………12

5.Спектры затухающих колебаний…………………………………….19

Выводы…………………………………………………………………..24

Список использованных источников…………………………………..25

Введение

Добротность - очень ёмкое понятие в теории колебаний. Дело в том, что любая одномерная колебательная система всегда характеризуется двумя основными параметрами: ω₀ - собственной частотой и β - коэффициентом затухания. Следует отметить, что понятие коэффициента затухания вводится при условии, что сила трения, действующая на осциллятор, пропорционально скорости F_сопр ~ rV («колебательное» трение). Если закон сопротивления другой, как, например, при колебаниях с сухим трением, то введение β затруднительно. Пусть указанные два параметра ввести можно; тогда можно ввести и их отношения ω_0/β₀ получим безразмерный параметр, который и называется добротностью. Иногда в частных исследованиях вводят величины, отличающиеся от ω_0/β на некоторый постоянный множитель. Но это ничего не меняет.

При указанных условиях уравнение колебаний имеет вид

x" + 2β x' + 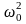x = 0 (1)

где ω₀ - круговая частота [рад/с], x'-первая производная координаты материальной точки по времени[м/с], x"-вторая производная координаты материальной точки по времени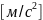 ,x – координата материальная точка [м], β – коэффициент затухания [с^-1]

Здесь на осциллятор действует только собственная возвращающая сила

F_в = - x и сила трения F_т = - 2β x', x(t) - любая колеблющаяся физическая величина: смещения частицы от положения устойчивого равновесия, сила тока в колебательном контуре, смещение столбика газа в акустическом резонаторе и т.д. К сожалению, в уравнении (1) нельзя ввести добротность.

Решением уравнения (1) является условие: 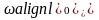> β является затухающая гармоника (рисунок. 1)

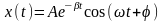, (2)

где A – амплитуда колебаний [м], t – время [с], – начальная фаза [рад]

Здесь 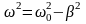, а величина 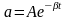может рассматриваться как переменная во времени амплитуда. Пусть τ - время, за которое амплитуда уменьшается в е раз, т.е.

A/a = = 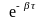, (3)

за это время осциллятор успевает совершить N_е колебаний

N_е = τ /Т = 1/(βТ); Т = 2π/ω.

Введем параметр

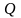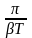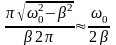= = πN_e = , (4)

где Т – период колебаний [с], Q – добротность осциллятора.

Q называется добротностью. Из (4) следует, что добротность в π раз больше числа колебаний, совершаемых за такое время, что амплитуда колебаний уменьшается в е раз.

Рассмотрим убыль энергии осциллятора при затухающих колебаниях (2). Запас механической энергии, е- запас механической энергии(Дж).

=

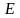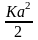
Отсюда

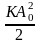
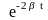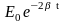= = , (5)

где K – жесткость пружины .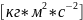

Здесь Е_о – начальный запас энергии в системе. Продифференцируем (5) по времени и определим скорость убыли энергии осциллятора.

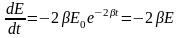; (6)

где Е_о - начальный запас энергии в системе (Дж), .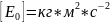

Будем считать период колебаний Т достаточно малым, таким, что Т ~ dt, что оправдано для высокодобротных колебаний, тогда изменение энергии за период ΔЕ из (6).

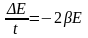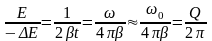; ; (7)

Таким образом, добротность осциллятора в 2π раз больше убыли его энергии за период.

3. Рассмотрим вынужденные колебания осциллятора и пусть внешняя вынуждающая сила F = F₀ cos₀ ωt будет гармонической. Тогда уравнение (1) преобразуется к виду

x" + 2β x' + x = 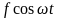; (8)

где f = 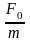- амплитуда (приведенная) внешней (вынуждающей) силы, ω – её частота.

Решение уравнения (8) в виде установившихся колебаний (без учета

переходного процесса) имеет вид

х(t) = А соs (ωt + φ), (9)

A(ω) = 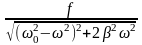; (10)

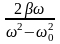tg φ = ; (11)

Функция А(ω) - амплитуда установившихся колебаний, она имеет максимум на резонансной частоте.

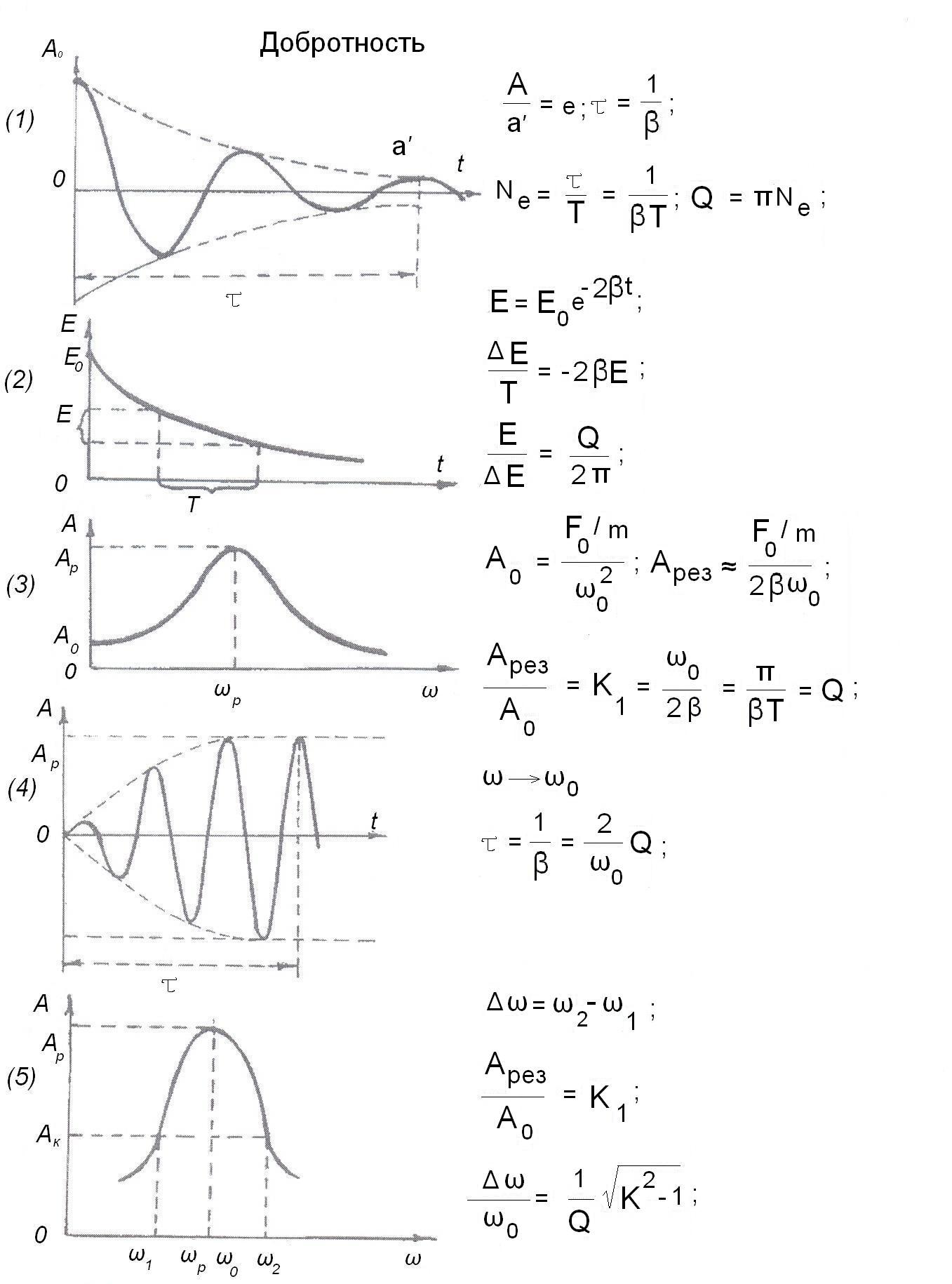
Добротность осцилляторов.

Обычный колебательный LC контур - 10²

Комертоны – 10⁴

Механические (резина) 10 на 100 Гц; 5 на 2*10³: 3 на 10⁴ Гц.

Акустические резонаторы - 50

Радиотехнические контуры с частотой ~ 1 МГц – n * 10²

Медные резонаторы СВЧ на частотах f > 1 МГц – 3 * 10⁴

Пьезоэлектрические кристаллы (кварц) – 5 * 10⁵

Колебания ядер атомов в эффекте Мессбауэра - 10¹⁰

Лазерные колебания (резонатор Фабри - Перо) – 5 * 10⁶

Пульсары (нейтронные замагниченные звезды) - 7,5 * 10¹²

(Период 0,033с, замедление вращения и частоты следования импульсов

36,52 нс/сутки = 4,23 * 10^-13. Период увеличивается в е раз за 2500 лет).

Нахождение добротности осциллятора

Рассмотрим задание на нахождение добротности осциллятора.

Рубиновый лазер излучает на l = 0,58 мкм. Ширина линии изменяется от 4,7 10^-2 до 4,7 10^-4 Ангстрем (А⁰). В каких пределах изменяется добротность лазера (резонатора Фабри-Перо).

Решение

Добротность 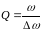, где w - частота (круговая) излучения, Dw - ширина резонансной кривой на полувысоте:

; ;

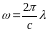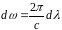Поэтому 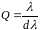, l = 0,58 мкм = 5800 А.

Точка совершает затухающие колебания с частотой ω = 25 с^-1. Найти коэффициент затухания β и добротность Q, если в начальный момент скорость точки равна 0, а её смещение из положения равновесия в η = 1,020 раза меньше амплитуды.

Решение

Будем исходить из уравнение затухающих колебаний:

;

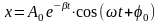Введём новую переменную y:

y = η;

;

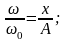
Отсюда выразим β:

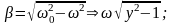
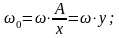
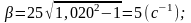
А добротность вычисляется в свою очередь по формуле:

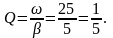
Ответ:

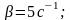
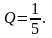
Порядок выполнения эксперимента

1. Установил угол α наклонного стержня относительно вертикали равный 0º, 30º, 45º, 60º последовательно.

2. Отклонил колеблющийся стержень на угол φ равный 20º, 30º, 40º последовательно.

3. С помощью секундомера засёк время t, в течении которого угол отклонения колеблющегося стержня φ уменьшился в 2 раза, т.е. амплитуда уменьшилась в 2 раза. Подсчитал количество колебаний за время t.

4. С помощью известных формул подсчитал β – коэффициент затухания колебаний, Q – добротность, T – период колебания стержня за время t, ω – частота колебаний стержня, ω₀ –собственная частота колебаний стержня, M_тр – момент трения, a – логарифмический декремент затухания.

5. Измерил m - массу, d - диаметр, r - радиус, h - ширину 2-х гаек, подшипника, колеблющегося стержня и l – длину стержня.