ЭЛЕКТРОМАГНЕТИЗМ.
Электромагнитные волны.
Волновое уравнение.
Рассмотрим
непроводящую однородную среду,
характеризуемую диэлектрической
проницаемостью
и магнитной проницаемостью
. Пусть в этой среде отсутствуют свободные
заряды и токи проводимости, т.е.
и
.
Кроме того,
и
,
иными словами, рассматриваемая область
не содержит ферромагнетиков.
Тогда система уравнений Максвелла принимает вид:
,
,
,
.
Перепишем уравнения для вихрей полей в виде
и
.
Продифференцируем первое уравнение по времени:
.
Применяя операцию
ко второму уравнению и подставляя
полученный из первого результат, находим
.
Из векторного анализа имеем
,
где
.
,
т.к.
из-за условия
.
Итак, имеем
,
и аналогично для
или
:
.
(6.1)
Уравнение вида
(6.2)
называется волновым
уравнением.
Здесь
.
Рассмотрим
одномерный случай, когда процесс
распространяется вдоль оси
.
Тогда
.
Решением этого
уравнения является функция вида
.
Это легко
проверить
;
и
;
.
Смысл приведенного решения прост
-
уравнение волны,
распространяющейся
вдоль (знак «минус») или против (знак
«плюс») оси
со скоростью
.
Действительно,
равенство
выполняется, если
,
или
,
т.е. имеет смысл скорости.
При фиксированных
значениях
и
значение функции
постоянно на всей плоскости, перпендикулярной
.
Поэтому такие волны называются плоскими.
Аргумент
функции
называется фазой
волны. Уравнение поверхности постоянной
фазы (волновой поверхности) имеет вид:
.
Дифференцируем
это уравнение по времени:
,
получаем
фазовая скорость, т.е. скорость, с которой поверхность с фиксированным значением фазы (волновая поверхность) перемещается вдоль оси .
Сравнивая в
(6.1) и (6.2) коэффициенты при вторых
производных по времени, находим, что
.
Т.о., электромагнитное
поле распространяется от места возбуждения
с конечной скоростью
.
Если - гармоническая функция (колебательный процесс), то она описывает гармоническую или монохроматическую волну. Волна называется монохроматической (по-гречески - одноцветной), если поле волны является гармонической (синусоидальной) функцией времени.
Волна, распространяющаяся в положительном направлении оси , описывается уравнениями
;
,
где
и
- амплитуды
волны:
- частота
электромагнитных колебаний или круговая
частота.
Вводя обозначение
,
где
- волновое
число (
,
т.е. равно числу длин волн, укладывающихся
на отрезке
см - отсюда его название), можем записать
или
.
Аргумент косинуса
называется фазой
волны;
- начальная
фаза.
Если зафиксировать
момент времени
,
то получаем синусоидальное распределение
полей
и
в пространстве (вдоль оси
) в данный момент времени.
Если зафиксируем значение координаты , по получим синусоидальное распределение полей и в
зависимости от времени - гармонические колебания с частотой .
Период изменения
напряженности поля в пространстве - это
длина волны
:
,
т.е. длина волны
представляет собой то расстояние, на
которое перемещается плоскость постоянной
фазы за время, равное одному периоду
колебаний
.
Описать плоскую монохроматическую волну можно иначе, используя более общий подход.
Зададим направление
распространения плоской волны с помощью
единичного вектора
,
направленного по
нормали к плоскости
постоянной фазы волны. Введем вектор
.
Вектор
,
направленный в сторону распространения
волны, называется волновым
вектором.
Теперь можно
записать
,
и, абстрагируясь от системы координат,
получаем
;
.
Эти уравнения описывают плоскую монохроматическую волну, распространяющуюся в направлении
вектора
.
Часто зависимость векторов электромагнитного поля от координат и времени удобно записывать в комплексной форме. Используем для перехода к комплексной форме записи формулу Эйлера:
.
Тогда общее решение волнового уравнения для плоской монохроматической волны можно представить в виде:
и
.
Знак «
»
мы, как это принято, в дальнейшем будем
опускать, не забывая при этом, что
физический смысл имеет лишь вещественная
часть используемых комплексных выражений:
и
.
Амплитуды и в общем случае являются комплексными величинами. Можно записать
,
где модуль равен
амплитуде колебаний, а аргумент -
начальной фазе колебаний в точке
.
Аналогично может быть представлена
комплексная амплитуда
.
Комплексная запись особенно удобна, как мы увидим далее, при применении к векторам и дифференциальных операторов.
Резюмируем сказанное выше.
Из уравнений Максвелла следует вывод о существовании принципиально нового физического явления: электромагнитное поле способно существовать самостоятельно, т.е. отдельно от электрических зарядов и токов. Изменение состояния электромагнитного поля носит волновой характер. Поля такого рода называют электромагнитными волнами.
Любая электромагнитная волна (гармоническая или электромагнитное возмущение произвольной формы) характеризуется следующими общими свойствами.
Основные свойства плоских электромагнитных волн.
1. Подставим уравнения плоских волн и в уравнения Максвелла.
:
;
;
т.е. уравнение
преобразуется к виду
.
Для упрощения
дальнейших вычислений заметим, что
дифференцирование по времени векторов
плоской волны сводится к умножению их
на
,
а дифференцирование по координате - к
умножению
на
.
Уравнение
таким же способом преобразуется к виду
.
Или
;
.
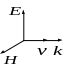Из полученных
уравнений следует, что в плоской
электромагнитной волне векторы
и
взаимно перпендикулярны и образуют
правовинтовую систему. Из
перпендикулярности
векторов
и
к волновому вектору
(скорости волны
),
т.е. направлению
распространения волны, следует, что электромагнитные волны — поперечные.
Это свойство следует также из уравнений и ,
которые преобразуются
к виду
и
,
соответственно.
2. Учитывая, что
входящие в уравнения векторы
,
(здесь учтено,
что
и
)
и
взаимно перпендикулярны, получаем, что
.
Т.о., отношение
численных значений векторов
и
от времени не зависит, т.е. эти векторы
имеют одинаковые фазы и изменяются
синхронно
(между мгновенными значениями
и
в любой точке существует определенная
связь
).
3. Выразим вектор из уравнения и подставим в уравнение .
Получаем
.
Расписывая
двойное векторное произведение по
правилу
,
имеем
,
т.к.
из-за
.
Получаем соотношение
,
откуда
и
.
Это так называемая
фазовая
скорость
электромагнитной волны, т.е. скорость
распространения колебаний одинаковой
фазы. В вакууме (
)
скорость распространения поля численно
равняется электродинамической постоянной,
определяющей силу взаимодействия токов
и имеющей размерность скорости. Значение
электродинамической постоянной,
найденное опытным путем, в пределах
ошибок эксперимента равно скорости
света в вакууме. Численное совпадение
этих величин служит доказательством
как электромагнитной природы света,
так и правильности уравнений Максвелла,
по крайней мере, в применении их к
вакууму.
Отметим, что в признании конечности скорости распространения поля заключается основное отличие фактического содержания теорий близкодействия и, прежде всего, теории Максвелла, от теорий мгновенного дальнодействия начала прошлого столетия.
4. Если в электромагнитной волне поведение векторов и в пространстве и времени подчиняется
определенному
закону, то такую волну называют
поляризованной.
Если направить
ось
системы координат вдоль волнового
вектора
,
то вследствие поперечности электромагнитных
волн векторы
и
будут иметь отличные от нуля проекции
только на оси
и
.
Уравнения Максвелла допускают, в частности, такое решение, когда каждый из векторов и совершает колебания только вдоль одной из взаимно перпендикулярных осей. Тогда говорят, что волна имеет линейную, или плоскую поляризацию. Плоскость, в которой лежит вектор напряженности
электрического поля волны и волновой вектор , называют плоскостью поляризации или плоскостью колебаний.
Линейной не исчерпываются виды поляризации волн. О других видах поляризации разговор пойдет ниже.