6

Электромагнетизм

Глава 2. Электростатика в веществе.

2.5. Проводники в электрическом поле.

1. Проводники.

Наиболее хорошими проводниками электричества являются металлы. Основные особенности проводников состоят в следующем:

1) В проводниках имеются свободные заряды, т.е. индуцированные заряды разделяются (могут быть разделены механически); в металлах свободными зарядами являются электроны.

2) В равновесном состоянии электрическое поле внутри проводника, находящегося во внешнем поле или заряженного до некоторого значения , равно нулю ( ).

В противном случае на электрические заряды в проводнике будет действовать со стороны поля сила, приводящая их в движение и вызывающая перераспределение зарядов. В электростатическом состоянии движение зарядов отсутствует, откуда следует, что электрическое поле внутри проводящего вещества должно быть равно нулю. Отсюда неизбежно получаем, что в стационарном состоянии в проводнике

и, следовательно, объемная плотность избыточных (нескомпенсированных) зарядов внутри однородного проводника также равна нулю.

Заметим, что мы имеем в виду поле, усредненное по объему, который велик по сравнению с характерными объёмами атомов.

3) Избыточный электрический заряд может располагаться только на поверхности проводника с некоторой

плотностью , вообще говоря, различной в разных точках его поверхности. Избыточный поверхностный

заряд находится в очень тонком слое у поверхности проводника (толщина слоя порядка одного – двух межатомных расстояний).

4) Отсутствие поля внутри проводника ( ), означает, что потенциал в объеме проводника одинаков во всех точках: , т.е. проводник представляет собой эквипотенциальную область пространства, а его поверхность – эквипотенциальную поверхность.

5) Напряженность поля в любой точке поверхности проводника направлена перпендикулярно к ней (иначе на поверхности проводника будут происходить движение зарядов до тех пор, пока не обратится в нуль тангенциальная составляющая поля ), т.е. .

Т.о., в состоянии равновесия тангенциальная составляющая поля внутри и вне проводника должна быть равна нулю.

Доказательство этого утверждения можно провести, используя теорему о циркуляции для вектора и выбрав для этой цели контур 1-2-3-4, как показано на рисунке:

(5.1)

Стороны и контура можно сделать сколь угодно малыми, вследствие чего интегралы по ним обращаются в нуль. Нулю также равен интеграл, взятый по участку контура , поскольку поле внутри проводника равно нулю. Тогда при интегрировании по стороне контура в силу (5.1) имеем . Поскольку сторона два может быть выбрана любой (малой) длины, то получаем, что .

6 ) Поле вблизи поверхности проводника. Пусть интересующий нас участок поверхности проводника граничит с вакуумом ( ). Линии вектора перпендикулярны поверхности проводника, поэтому в качестве замкнутой поверхности возьмем небольшой цилиндр, расположив его, как показано на рисунке. Теорему Гаусса для выбранной цилиндрической поверхности, вырезающей на поверхности проводника площадку с плотностью стороннего заряда , можем записать в виде:

. (5.2)

Т.к. через нижнее основание и боковую поверхность поток вектора (из-за внутри проводника и ) равен нулю, то

,

или

. (5.3)

В СИ:

Дополнение

Скачок нормальной составляющей вектора на поверхности проводника можно (полезно) объяснить, используя другой подход – рассматривая суперпозицию полей. Полное поле, описываемое вектором , складывается из электрического поля , создаваемого зарядами, расположенными на маленькой площадке, которую можно выделить на поверхности , и поля , возбуждаемого всеми остальными зарядами, находящимися на рассматриваемой поверхности. Мысленно удалим с поверхности площадку . Тогда внешнее по отношению к ней поле изменяется в “дырке” - непрерывно (см. рисунок). Поле (у поверхности) находится по т. Гаусса как поле бесконечной равномерно заряженной плоскости, равно и направлено, как показано на рисунке.

Тогда в силу принципа суперпозиции поля по обе стороны поверхности равны, соответственно:

(5.4)

Вводя общую внешнюю нормаль ( и ), получаем, что при переходе поверхности электрическое поле изменяется скачком на величину:

. (5.5)

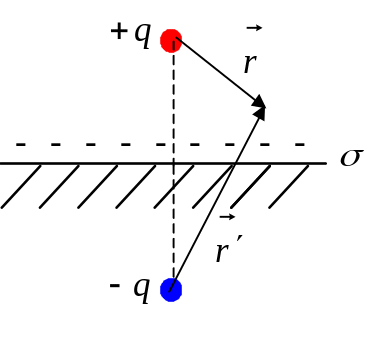
2.5.2. Метод электрических изображений.

Пусть имеется плоская проводящаяся поверхность, простирающаяся в бесконечность. Припишем этой плоскости нулевой потенциал. Расположим теперь точечный заряд над плоскостью на оси на расстоянии вблизи её поверхности. Поверхностную плотность наведенного (индуцированного) заряда и поле вблизи проводящей поверхности можно вычислить двумя способами.

1) Мы предполагаем, что положительный заряд будет индуцировать на поверхности отрицательный заряд, плотность которого меняется с расстоянием (отсчет ведется от точки на плоскости, куда проецируется заряд – см. рисунок). Очевидно, что картина должна быть симметричной относительно оси .

Напряженность результирующего поля определяется как векторная сумма напряженностей полей, создаваемых точечным зарядом и наведенным зарядом, распределенным по плоскости с плотностью , причем нормальные составляющие векторов и в полупространстве над плоскостью складываются, а под поверхностью - вычитаются, причем так, что поле в нижнем полупространстве равно нулю.

Используя соотношения (5.3) и (5.4), получаем для нормальной компоненты поля (тангенциальные, как было показано выше, равны нулю) над плоскостью:

. (5.6)

Знак “– “ в выражении (5.6) указывает на то, что направление нормальной компоненты вектора напряженности электрического поля вблизи плоскости противоположно оси .

Соответственно, в нижнем полупространстве:

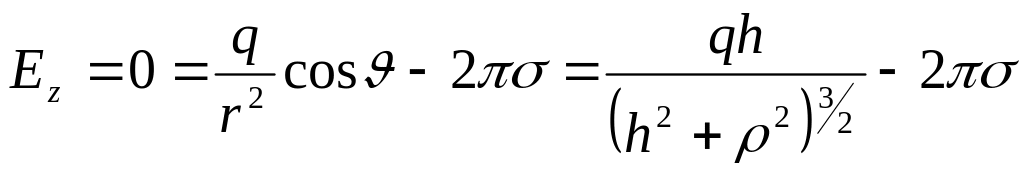. (5.7)

Складывая два последних выражения, находим напряженность поля и поверхностную плотность заряда:

. (5.8)

Если мы просуммируем заряд, индуцированный на плоскости, то получим заряд “ ”. В самом деле:

(5.9)

2) Результат, полученный в (5.9), приводит к весьма любопытным выводам. Оказывается, что то же электрическое поле можно получить, заменив плоскость с распределенными на ней наведенными зарядами точечным зарядом , помещенным на оси на расстоянии (см. рисунки) в нижнем полупространстве. Действительно, вблизи поверхности получаем

(5.10)

В этом методе – “методе изображений” – результирующее поле в любой точке “верхнего” полупространства находится как сумма полей от «истинного» и «фиктивного» зарядов:

. (5.11)

Особо подчеркнем, что “действие”, фиктивного заряда распространяется лишь на то полупространство, в котором находится действительный заряд . В “нижнем” полупространстве поле отсутствует.

Рассмотренный в пункте 2) способ расчета – это искусственный метод для расчета взаимодействия проводников с зарядами и другими полями, позволяющий в ряде случаев (весьма ограниченном) рассчитать электрическое поле достаточно просто.

В общем случае идея предложенного метода формулируется следующим образом.

Пусть имеется система точечных зарядов и пусть – эквипотенциальная поверхность, разделяющая пространство на два полупространства и (см. рис). Задание зарядов и потенциала на поверхности однозначным образом определяет электрическое поле в полупространстве и, аналогично, в полупространстве .

По теореме единственности (уравнение имеет единственное решение) поле определяется однозначно. Поэтому, если сделать поверхность проводящей, то поле во всем пространстве не изменится, т.к. поля в подпространствах и независимы. Тогда поле в полупространстве можно получать двумя эквивалентными способами:

1. либо как сумму полей, создаваемых зарядоми и зарядами, наведенными на поверхности ;

2. либо как сумму полей, создаваемых зарядом и «фиктивным» зарядом , имея при этом в виду, что поле фиктивного заряда распространяется только на то полупространство, в котором находится действительный заряд.

По существу рассматриваемый метод основан на подгонке потенциала под граничные условия: мы стараемся подобрать такую конфигурацию фиктивных зарядов, у которой конфигурация поля в интересующей нас части пространства была бы той же. Если этого удается достичь с помощью достаточно простой конфигурации, то метод изображений оказывается весьма эффективным.

Совокупность зарядов рассматривается как «зеркальное изображение» электрических зарядов в проводнике, ограниченном поверхностью . Отсюда способ расчета взаимодействия зарядов с проводниками и полей вблизи проводников получил название «метод электрических изображений».

Применение метода электрических изображений для решения определенного круга задач электростатики обосновано теоремой единственности: поскольку полученное таким решение задачи удовлетворяет уравнению Пуассона и граничным условиям, то оно является правильным и единственным.