33. Ряди Фур'є сигналів s(t) в просторі l2(0,t). Розклад сигналів по тригонометричній системі функцій. Формули визначення коефіцієнтів ряду Фур'є.

Ряд Фур'є — в математиці — спосіб представлення довільної складної функції сумою простіших. В загальному випадку кількість таких функцій може бути нескінченною, при цьому чим більше таких функцій враховується при розрахунку, тим вищою стає кінцева точність представлення даної функції. В більшості випадків в якості найпростіших використовуються тригонометричні функції синуса і косинуса. В цьому випадку ряд Фур'є називаеться тригонометричним, а обчислення такого ряду часто називають розкладом на гармоніки.

Класичне визначення

Тригонометричним рядом Фур'є називають функційний ряд виду

Якщо ряд збігається, то його сума дорівнює періодичній функції f(x) з періодом 2π, оскільки sinnx та cosnx є періодичними з періодом 2π.

Сталі числаa₀, a_n, b_n (n ∈ N) називаються коефіцієнтами тригонометричного ряду:

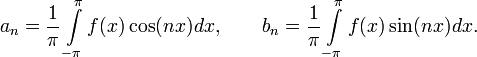
Загальне визначення

Нехай дано ортогональну систему в Гільбертовому просторі R {φ₁, φ₂, … φ_n, …} та f — довільний елемент з R. Послідовність чисел

називається координатами, або коефіцієнтами Фур'є елемента f по системі { φ_k}, а ряд

називається рядом Фур'є елемента по ортогональній системі { φ_k}.

34. Розподіл ймовірності часу обслуговування заявок. Механізм обслуговування заявок.

Механізм обслуговування.

Обслуговуючий механізм характеризується тривалістю процедур обслуговування і кількістю вимог, які обслужені в результаті виконання кожної такої процедури. У наведеному вище прикладі, де мова йшла про обслуговування клієнтів у перукарні або в ресторані, процедура обслуговування вважається завершеною, коли клієнт (а у випадку обслуговування в ресторані, можливо, і ціла група клієнтів) залишає відповідний заклад після надання йому послуг. Тривалість інтервалу часу, необхідного для реалізації процедури обслуговування, частково залежить від запитів клієнта (або групи клієнтів). Але вона може залежати також і від стану самої обслуговуючої системи: так, наприклад, обслуговуючий персонал може форсувати процедури обслуговування, якщо обслуговування очікує велике число клієнтів. Як і тривалості інтервалів між надходженнями вимог, тривалості обслуговування в кожній з обслуговуючих точок можуть (хоча це і не обов’язково) описуватися за допомогою незалежних випадкових змінних з ідентичними розподілами вірогідностей їхніх чисельних значень. У ряді випадків необхідно також враховувати вірогідність виходу обслуговуючого приладу з ладу після закінчення деякого обмеженого інтервалу часу.

Для описання механізму обслуговування потрібно також зазначити кількість і взаємне розташування обслуговуючих приладів або каналів.

Так, наприклад, прилетівши з Нью-Йорка в аеропорт Лондона, пасажир повинен пройти там паспортну перевірку. При цьому всі пасажири вишиковуються в одну лінію і кожен із пасажирів, що дочекалися своєї черги, скеровується до одного з чиновників, що звільнилися і виконують перевірку паспорта (єдина черга).

Цілком інша картина спостерігається, наприклад, у години пік на вокзалі біля білетних кас, коли черги утворюються до всіх без винятку касирів. У цьому випадку відвідувач повинен обрати одну з черг і очікувати обслуговування з боку цілком визначеного касира. Якщо Ваш вибір виявився невдалим, перебування в черзі може забрати у Вас навіть більше часу, ніж у деяких із тих, що прийшли після Вас, яким пощастило стати в „швидші” черги. (Якщо черги не занадто великі, можна перейти від обраного спочатку вікна до іншого, біля якого черга стала коротшою).

У кожному з наведених вище прикладів прилади (або канали) функціонують паралельно. Існує також множина СМО, у яких прилади розташовані послідовно, так що клієнт змушений переходити від одного приладу до іншого, іноді простоюючи біля кожного з них у черзі. До таких систем належать, наприклад, підприємство з дрібносерійним виробни­цтвом, де для виготовлення партії замовлених виробів вони повинні пройти послідовне опрацювання в ряді цехів.

35. Рівність Парсеваля, нерівність Бесселя, їх енергетичний зміст.

Справедлива так звана нерівність Бесселя:

Якщо виконується рівність Парсеваля

то нормована система називається замкненою.

Справедливе твердження: в сепарабельному евклідовому просторі R будь-яка повна ортогональна нормована система є замкненою і навпаки.

39. Амплітудний і фазовий спектри сигналів, їх роль в ТАУ.

Амплітудний і фазовий спектри. Послідовність коефіцієнтів , яка входить в (6), називають амплітудним спектром функції (сигналу). Амплітудний спектр зручно зображати у вигляді дискретного графіка, показаного на рисунку 1, де у відповідність частотам поставлені коефіцієнти .

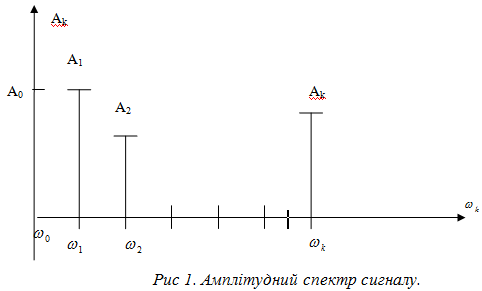
Послідовність фаз , які входять в ряд (6), називають фазовим спектром функції. Фазовий спектр функції теж зображають графічно у вигляді, наведеному на рисунку 2.

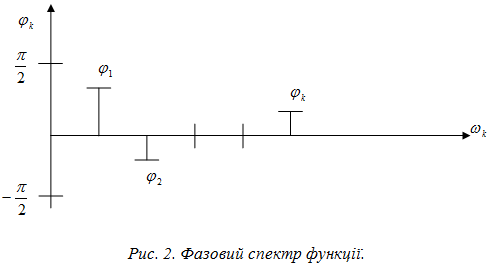
Амплітудний і фазовий спектри використовуються при розв’язуванні багатьох задач систем управління, зокрема, при визначенні амплітудного і фазового спектрів вхідного та вихідного сигналів системи; при визначенні комплексної передаточної функції системи та її ланок тощо.

41. Комплексна форма ряду Фур'є

Вираз називається комплексною формою ряда Фур'є функції f(x), якщо визначається рівністю

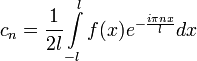, де n=0, ±1, ±2, …

Перехід від ряду Фур'є в комплексній формі до ряду в дійсній формі і навпаки виконується за допомогою формул:

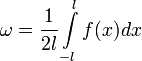
a_n = 2Rec_n

b_n = 2Imc_n

a₀ = 2c₀

(n = 1,2,...)

(40. Математичне сподівання і дисперсія інтенсивності вхідного потоку.)

42. Дослідження часу обслуговування заявок методами математичної статистики. Оцінка математичного сподівання і дисперсії часу обслуговування заявок.

Оцінка математичного сподівання:

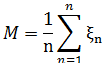
Дисперсія:

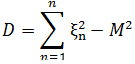
Середньо квадратичне відхилення:

43. Перетворення Фур'є (пряме і зворотнє), його роль в ТАУ. Перетворення Фур'є найпростіших сигналів. Властивості перетворення Фур'є.

Пряме перетворення Фур’є:

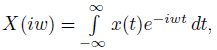
Зворотне перетворення:

Облишивши математикам доказ того, що при послідовному застосуванні прямого і оберненого перетворення Фур'є, початкова функція залишається незмінною, зосередимося на використанні перетворень Фур'є.

Перетворення Фур'є застосовуються для отримання частотного спектру неперіодичної функції, наприклад, електричного сигналу, тобто для представлення сигналу у вигляді суми гармонічних коливань. При цьому використовується властивість згортки.

Властивості

Хоча формула, що задає перетворення Фур'є, має ясний сенс тільки для функцій класу L₁(R), перетворення Фур'є може бути визначено і для більш широкого класу функцій, і навіть узагальнених функцій. Це можливо завдяки ряду властивостей перетворення Фур'є:

• Перетворення Фур'є є лінійним оператором:

• Справедливо рівність Парсеваля: якщо,

то перетворення Фур'є зберігає L₂-норму:

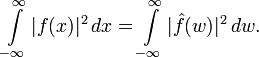
Ця властивість дозволяє по безперервності поширити визначення перетворення Фур'є на весь простір L₁(R). Рівність Парсеваля буде при цьому справедливо для всіх .

• Формула звернення:

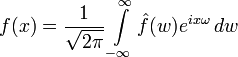
справедлива, якщо інтеграл в правій частині має сенс. Зокрема, це вірно, якщо функція f є досить гладкою. Якщо , то формула також вірна, оскільки рівність Парсеваля дозволяє надати інтегралу в правій частині сенс за допомогою граничного переходу.

Ця формула пояснює фізичний зміст перетворення Фур'є: права частина - (нескінченна) сума гармонійних коливань e^iωx з частотами ω, амплітудами і фазовими зрушеннями argf (ω) відповідно.

• Теорема про згортку:

якщо , тоді

, Де

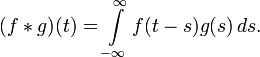
Ця формула може бути поширена і на випадок узагальнених функцій.

• Перетворення Фур'є та диференціювання.

Якщо , то

З цієї формули легко виводиться формула для n-й похідної:

Формули вірні і у випадку узагальнених функцій.

• Перетворення Фур'є і зсув.

Ця і попередня формула є окремими випадками теореми про пакунку, так як зсув по аргументу - це згортки з зрушено дельта-функції δ (x - x0), а диференціювання - згортки з похідної дельта-функції.

• Перетворення Фур'є і розтягування.