Трансформатор

Являє собою магнітопровід, на якому виконані 2 або більше обмотки. По магнітопроводу замикається магнітний потік Ф_М, що забезпечує магнітний зв'язок між обмотками. Існують потоки розсіювання Ф_S1 і Ф_S2, створювані струмами i₁, і i₂, що не замикаються по магнітопроводу й не є спільними для обмоток. Обмотки мають омічні опори r₁ і r₂, а також інші паразитні параметри, наприклад, між виткові та міжобмоточні ємності.

Ідеальний трансформатор представляється елементом, у якому відсутні потоки розсіювання, активні опори обмоток, паразитні ємності. Індуктивність намагнічування дорівнює безкінечності, тобто струм намагнічування дорівнює 0. При цьому обмотки пронизують однакові потоки й за законом електромагнітної індукції для обох обмоток можна записати, що:

Рис. 15

де n=w₂/w₁ — коефіцієнт трансформації трансформатора.

Із закону збереження енергії випливає, що:

Цей ж висновок можна одержати, використовуючи закон повного струму з урахуванням тієї обставини, що i_μ=0:

При зазначених допущеннях трансформатор можна представити еквівалентною схемою, зображеною на рис. 16:

Рис. 16

Модель проста, однак застосовується вкрай рідко, тому що не дозволяє врахувати принципово важливих для трансформатора явищ – нагромадження енергії в магнітопроводі й необхідність відновлення магнітного стану осердя. Для її врахування представляють трансформатор ідеальним елементом, у якому відсутні потоки розсіювання, але є скінченна величина індуктивності намагнічування L_μ. Остання визначає струм намагнічування, що протікає по первинній обмотці, і приводить до еквівалентної схеми у вигляді рис. 17:

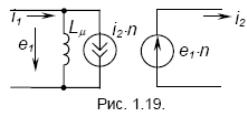
Рис. 17

У ряді випадків, особливо при розрахунку досить простих кіл, представляється зручним «привести» трансформатор до однієї зі сторін: первинної або вторинної, представивши процес передачі енергії через магнітопровід безпосереднім підключенням навантаження до кола джерела енергії. Якщо, наприклад, трансформатор навантажений на активний опір R₂, то величина струму навантаження в первинному колі визначиться:

Тоді еквівалентний опір навантаження, підключеної до первинного кола, дорівнює:

Нескладно показати, що індуктивність, включена як навантаження, приводиться до первинної сторони у вигляді:

Ємність – відповідно до співвідношення:

У такий спосіб, еквівалентна схема «приведеного» до первинної обмотки трансформатора має вигляд (рис. 18):

Рис. 18

Виконання трансформатора із осердям з магнітопроводу у вигляді феромагнетику приводить до нелінійної залежності L(i).

Наведені моделі трансформатора є низькочастотними, тому що не враховують вплив індуктивностей розсіювання і ємностей між обмотками. Повна еквівалентна схема трансформатора, наведена до первинного ланцюга має вигляд рис. 19:

Рис. 19

Тут L_S1, L_S2’ — індуктивність розсіювання первинної обмотки й приведена до первинної індуктивність розсіювання вторинної обмотки; C₁, C₂’ — ємність первинної й приведена до первинної ємність вторинної обмотки; C₁₂ — ємність між первинною й вторинною обмотками, R_μ - еквівалентний опір, що відображає втрати в магнітопроводі.

Як правило, індуктивності розсіювання не мають істотного впливу на процеси в колах намагнічування, тому є можливим об'єднати індуктивності розсіювання в одну. Те ж справедливо й для резисторів, що відображають омічні втрати в обмотках. Тому для підвищувального трансформатора n>>1 еквівалентна схема трансформатора має вигляд рис. 20, для понижувального — відповідно, рис. 21:

Рис. 20 Рис. 21