7.1.3 Контроль за модулем

Контроль виконання арифметичних і логічних операцій можна здійснювати за допомогою контрольних кодів, що представляють собою залишки від ділення чисел на деякий модуль. Такий контроль називається контролем по модулю. Для двійкових чисел цей модуль звичайно дорівнює або більше 3. Розрізняють числовий і цифровий контроль за модулем. При числовому методі код заданого числа визначається як найменший позитивний залишок від ділення числа на обраний модуль.

7.1.4. Контроль арифметичних операцій

Арифметичні операції можна представити у вигляді послідовності наступних елементарних операцій: передача слова, зсув, взяття зворотного коду, складання. Операцію зсуву можна представити як передачу слова з i-того розряду в (i + x)-ті або (ix)-ті розряди. Тому, контроль зсуву можна здійснити за методом парності-непарності. Контроль виконання арифметичних операцій (додавання, віднімання, множення) можна здійснити методом контролю за модулем. Одночасно з виконанням операції над числами та ж операція виробляється над їх контрольними кодами, і контрольний код результату основної операції порівнюється з результатом операції над контрольними кодами вихідних чисел. При розбіжності фіксується помилка.

8.1.Способи задання Булевих функцій

8.1.1. Метод мінімізації Квайна

Вихідною формою подання функції для мінімізації за методом Квайна є досконала диз'юнктивна нормальна форма (ДДНФ). Метод забезпечує одержання скороченої ДНФ (СДНФ), тобто сукупності всіх простих імплікант.Метод базується на використанні співвідношення неповного склеювання

і співвідношення поглинання

де A і B - довільні кон'юнктивні терми, x - змінна.

8.1.2. Метод мінімізації Квайна - Мак-Класкі

Метод Квайна - Мак-Класки є модифікацією методу Квайна. Він ґрунтується на співвідношеннях неповного склеювання і поглинання, як і метод Квайна. Особливістю методу є використання цифрової форми запису перемикальних функцій. В цьому випадку зменшується число символів для подання термів і число операцій в процесі мінімізації, що робить метод зручним при програмній реалізації. Якщо використовувати геометричну інтерпретацію подання перемикальних функцій, то кожен набір аргументів є n-вимірним вектором (n - число аргументів) і визначає точку n-вимірного простору. Сукупність усіх наборів зображає n-вимірний куб. Конституентам відповідають вершини куба, а імплікантам - ребра і грані. Кожній конкретній функції відповідає певне просторове зображення.

8.1.3. Мінімізація булевих функцій методом Петрика

Петрик формалізував другий етап методу Квайна. Даний метод дозволяє звести роботу з імплікантною матрицею до роботи з аналітичним виразом. По імплікантній матриці будується кон'юктивне представлення даної матриці:

1. всі прості імпліканти позначаються буквами

2. для кожного i-го стовпця матриці будується диз'юнкція всіх букв, що позначають рядки матриці, перетини яких з i-тим стовпцем відмічено хрестиком.

3.кон'юнкція, побудована на диз'юнкції всіх стовпців матриці, і є кон'юктивним представленням імплікантної матриці. До отриманого виразу можуть бути застосовані всі співвідношення булевої алгебри з метою його спрощення. Після розкриття дужок і всіх можливих поглинань отримаємо диз'юнкцію кон'юнкцій, кожна з яких містить імпліканти тупикових функцій.

Розділ ІІ – Розрахункові дані

Вихідні дані для курсової роботи представлені у вигляді двох десяткових чисел А(10) і В(10) в таблиці:

Номер завдання – 14

	4
1	а=176 b=439

1.1.Перевести числа А(10) і В(10) в двійкову систему числення по загальному правилу переводу, а також через вісімкову систему числення.

1.1.1. По загальному правилу переводу:

а) А₁₀  А₂;

176 2

176 88 2

0 88 44 2

0 44 22 2

0 22 11 2

0 10 5 2

1 4 2 2

1 2 1

0

а₂=10110000

б) b₁₀  b₂;

4 39 2

438 219 2

1 218 109 2

1 108 54 2

1 54 27 2

0 26 13 2

1 12 6 2

1 6 3 2

0 2 1

1

b₂=110110111

1.1.2.Через вісімкову систему числення

а) А₁₀  А₈ А₂;

176 8

176 22 8

0 16 2

6

А₈=260

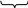010 110  000

2 6 0

А₂=010110000

б) В₁₀  В₈ В₂;

439 8

432 54 8

7 48 6

6

В₈=667

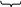
110   110  111 

6 6 7 В₂=110110111

2.1. Записати десяткові дроби і перевести їх в двійкову систему числення з точністю 11 двійкових знаків по загальному правилу переводу, а також через вісімкову систему числення . Записать дроби в комірку машини з фіксованою точкою і кількістю розрядів n=10. Оцінити діапазон і точність представлення чисел при прийнятій розрядності.

2.1.1. Записати числа a₁₀ і b₁₀ у вигляді а₁₀·10 ^-3 і b₁₀·10 ^-3.

а₁₀  а₁₀·10 ^-3 = 0,176

b₁₀  b₁₀·10 ^-3 = 0,439

2.1.2. Перевести їх в двійкову систему числення з точністю 11 двійкових знаків по загальному правилу переводу

а) А₁₀ А₂;

0,	176×2
0	352×2
0	704×2
1	408×2
0	816×2
1	632×2
1	264×2
0	528×2
1	056×2

А₂=0,000101101

б) В₁₀  В₂;

0,	439×2
0	878×2
1	756×2
1	512×2
1	024×2

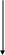
В₂=0,000000111

2.1.3. Перевести їх в двійкову систему числення з точністю 11 двійкових знаків через вісімкову систему числення:

а) А₁₀ А₈ А₂;

0 ,	176×8
1	408×8
3	264×8
2	112×8
0	896×8

А₈=0,1320

001  011  010  000

1 3 2 0

а₂=0,001011010000

б) В₁₀  В₈ В₂;

0 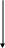,	439×8
3	512×8
4	096×8
0	768×8

В₈=0,340

011 100  000 

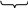
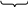
3 4 0

b₂=0,011100000

2.1.4. Записати дроби а₁₀·10 ^-3 і b₁₀·10 ^-3 в комірку машини з фіксованою точкою і кількістю розрядів n=10.

0,	0	0	1	0	1	1	0	1	0
0,	0	1	1	1	0	0	0	0	0

3.1.Представити дроби з різною комбінацією знаків (+a; +b; -b; -a)в прямому, зворотному і додаткових кодах

а) +a, -а;

+а

Прямий	0,	0	0	0	1	0	1	1	0	1
Зворотній	0,	0	0	0	1	0	1	1	0	1
Додатковий	0,	0	0	0	1	0	1	1	0	1

-а

Прямий	1,	0	0	0	1	0	1	1	0	1
Зворотній	1,	1	1	1	0	1	0	0	1	0
Додатковий	1,	1	1	1	0	1	0	0	1	1

б) +b, -b;

+ b

Прямий	0,	0	0	0	0	0	0	1	1	1
Зворотній	0,	0	0	0	0	0	0	1	1	1
Додатковий	0,	0	0	0	0	0	0	1	1	1

- b

Прямий	1,	0	0	0	0	0	0	1	1	1
Зворотній	1,	1	1	1	1	1	1	0	0	0
Додатковий	1,	1	1	1	1	1	1	0	0	1

4.1. Виконати операцію додавання (+a +b); (+a -b); (-a +b); (-a -b); у вказаних кодах.

4.1.1. (+a +b);

а_пр+ b_пр= а_зв+ b_зв= а_дод+ b_дод

0,000101101

0,000000111

0,000110100

4.1.2. (+a -b);

а) а_пр+(-b_пр)

0,000101101

1,000000111

1,000110100

б) а_зв+(-b_зв)

0,000101101

1,11111000

0,000100101

+ 1

0,000100110

в) а_дод+(-b_дод)

0,000101101

1,111111001

0,000100110

4.1.3. (-a +b);

а) -а_пр+ b_пр

1,000101101

0,000000111

1,000110110

б) –а_зв+ b_зв

1,111010010

0,000000111

1,111011001

в) –а_дод+ b_дод

1,111010011

0,000000111

1,111011010

4.1.4 a -b);

а) -а_пр+(- b_пр)

1,000101101

1,000000111

1,000110100

б) –а_зв+(- b_зв)

1,111010010

1,111111000

1,111001010

1

1,111001011

в) –а_дод+(- b_дод)

1,111010011

1,111111001

[1]1,111001100

5.1. Виконати операцію множення дробів по відомим чотирьом схемам множення, а також в додатковому коді по одній із схем множення.

5.1.1.Метод І – з сувом вправо

0,000101101

0,000000111

000101101

000101101

000101101

000000000

000000000

000000000

000000000

000000000

000000000

0,00100111011000000

Метод ІІ – з сувом вліво

0,000101101

0,000000111

000101101

000101101

000101101

000000000

000000000

000000000

000000000

000000000

000000000

0,00000000100111011

Метод ІІІ – Множення з старшого розряду a*b, з сувом вправо

0,000101101

0,000000111

000000000

000000000

000000000

000000000

000000000

000000000

000101101

000101101

000101101

0, 00000000100111011

Метод ІV - Множення з старшого розряду a*b, з сувом вліво

0,000101101

0,000000111

000000000

000000000

000000000

0000000000

000000000

000000000

000101101

000101101

000101101

0,00100111011000000

5.1.2. В додатковому коді по одній із схем множення

0,111010011

0,111111001

111010011

000000000

000000000

111010011

111010011

111010011

111010011

111010011

111010011

1,00100001011101101

6.1. Виконати операцію ділення двійкових дробів з встановленням залишку

101101 111

111 110

1000

111

0011

7.1. Виконати контроль по модулю 3 всіх арифметичних операцій.

а = 0,000101101

000 101 101 = =

0 5 5

а=

b=0,000000111

000 000 111 = 7 = 7*8 =7

0 0 7

b = 7

а= \3=15остача 0

b = 7 \3=2 остача 1

В прямому коді

a mod 3 = 0,00₂

b mod 3 = 0,01₂

- a mod 3 = 1,00₂

- b mod 3 = 1,01₂

В зворотному коді

a mod 3 = 0,00₂

b mod 3 = 0,01₂

- a mod 3 = 1,11₂

- b mod 3 = 1,10₂

В додатковому коді

a mod 3 = 0,00₂

b mod 3 = 0,01₂

- a mod 3 = 1,10₂

- b mod 3 = 1,11₂

В прямому коді

+ a + b = 0,00 + 0,01 = 0,01₂

+ a – b = 0,00 – 0,01 = 1,01₂

- a + b = -0,00 + 0,01 = 0,01₂

- a – b = 0,00 + 0,01 = 0,01₂

a*b = 0,00*0,01 = 0,00₂

a\b = 0,00₂

В зворотному коді

+ a + b = 0,00 + 0,01 = 0,01₂

+ a – b = 0,00 – 0,01 = 1,01₂

- a + b = -1,11 + 0,01 = 0,01₂

- a – b = 1,11 + 1,10 = 1,01₂

В додатковому коді

+ a + b = 0,00 + 0,01 = 0,01₂

+ a – b = 0,00 + 0,01 = 0,01₂

- a + b = 1,00 + 0,01 = 0, 01₂

- a – b = 1,00 + 1,11 = 1,11₂

-а*(-b) = 1,00 *1,11 = 0,00₂

8.1. Результати всіх арифметичних операцій перевести в десяткову систему числення по загальному правилу переводу, через вісімкову систему числення, а також за допомогою запису числа у вигляді степеневого ряду.

а = 0,000101101 =

000 101 101 = =

0 5 5

b=0,000000111= 7

000 000 111 = 7 = 7*8 =7

0 0 7

+ a + b = 0,00011 0100 = 52

000 110 100 = =

0 6 4

+ a – b = 0,000100010 = 34

000 100 010 = =

0 4 2

- a + b = 1,000100010 = - 34

000 100 010 =

0 4 2

- a – b = 1, 000110100 = 52

000 110 100 =

0 6 4

a*b = 0,000100111011 = 315

000 100 111 011 =

0 4 7 3

a\b = 0,110 = 6

110 =

6

9.1. Виконати всі арифметичні операції в десятковій системі числення.

a = 45

b = 7

+ a + b = 45 + 7 = 52

+ a – b = 45 -7 = 38

- a + b = - 45 + 7 = - 38

- a – b = - 45 – 7 = - 52

a*b = 45*7 = 315

a\b = 45\7 ≈ 6

10.1. Записати підряд двійкові числа А(2) і В(2) . Перші 16 цифр отриманого запису прийняти за значення булевої функції чотирьох змінних і представити її в табличному вигляді.

a=176

b=439

176 2

176 88 2

0 88 44 2

0 44 22 2

0 22 11 2

0 10 5 2

1 4 2 2

1 2 1

0

а₂=10110000

4 39 2

438 219 2

1 218 109 2

1 108 54 2

1 54 27 2

0 26 13 2

1 12 6 2

1 6 3 2

0 2 1

1

b₂=110110111

1011000011011011

				Y
0	0	0	0	1
0	0	0	1	0
0	0	1	0	1
0	0	1	1	1
0	1	0	0	0
0	1	0	1	0
0	1	1	0	0
0	1	1	1	0
1	0	0	0	1
1	0	0	1	1
1	0	1	0	0
1	0	1	1	1
1	1	0	0	1
1	1	0	1	0
1	1	1	0	1
1	1	1	1	1

11.1. Виписати всі функції, які покривають задану.

12.1. Записати в аналітичному виді ДДНФ заданої функції і мінімізувати її методом Квайна (безпосередньо по імплікантній матриці і з допомогою метода Петрика для пошуку тупикових ДНФ), методом Квайна – Мак-Класкі, а також за допомогою діаграм Вейча (карт Карно).

ДДНФ:

V V V

12.1.1. Мінімізація методом Квайна

Функція у досконалій диз’юнктивній нормальній формі (ДДНФ) має вигляд:

V V V

Виконавши попарне склеювання конституент одиниці, одержуємо множину імплікант 3-го рангу:

Подальше склеювання імплікант не можливе. Тоді функцію можна записати у вигляді:

V

	⌐x4⌐x3⌐x2⌐x1	⌐x4⌐x3x2⌐x1	⌐x4⌐x3x2x1	x4⌐x3⌐x2⌐x1	x4⌐x3⌐x2x1	x4⌐x3x2x1	x4x3⌐x2⌐x1	x4x3x2⌐x1	x4x3x2x1
	+	+
	+			+
		+	+
			+			+
				+			+
					+	+
						+			+
							+	+
								+	+

Таблиця покриттів:

Ядро

12.1.2. Мінімізація методом Квайна – Мак – Класкі

	0000	0010	1000	0011	1001	1100	1011	1110	1111
00x0	+	+
x000	+		+
001x		+		+
100x			+		+
1x00			+			+
x011				+			+
10x1					+		+
11x0						+		+
1x11							+		+
111x								+	+

12.1.3.Мінімізація методом Діаграм Вейча(Карт Карно)

Х₂

3	6	5
	9
	8	7
2		4	1

Х₁

Х₄

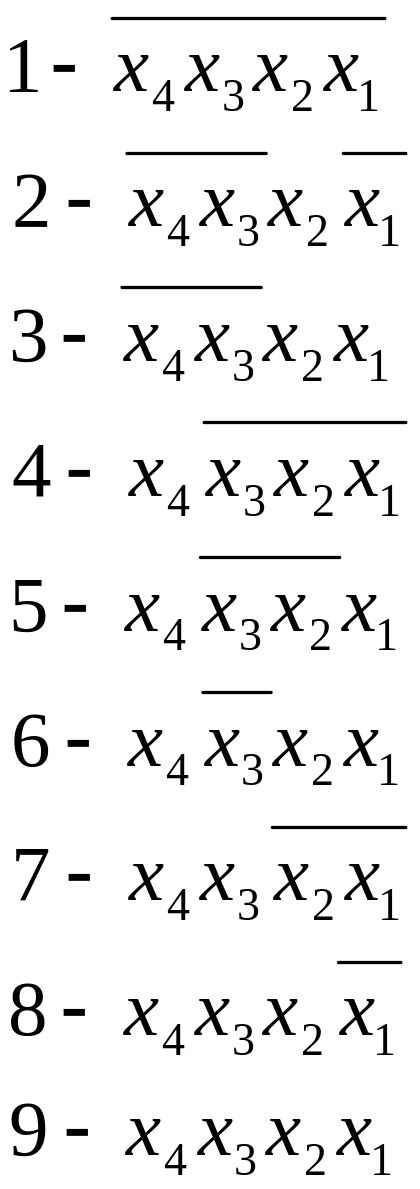
V

ДДНФ = V

Висновок

Завдяки курсовій роботі я розширила, узагальнила і закріпила на практиці знання, вміння і навички, отримані мною за період навчання . В завданні розглянула питання представлення чисел , алгоритми виконання основних арифметичних операцій та їх контролю.

Список використаної літератури

1. К.Г.Самофалов, А.М.Романкевич, В.Н.Валуйский. Прикладна теорія цифрових автоматів. К. Вища школа , 1987 – 375с.

2. Савельев А.Я. Прикладна теорія цифрових автоматів. М. 1987. -286с.

3. Куліковський Л.Ф., Мотов В.В. Теоретичні основи інформаційних процесів. М., 1987 – 248с.

4. В. І. Жабін , І. А. Жуков. Прикладна теорія цифрових автоматів. М. 2009. -300с

5. Кочубей О.О., Сопільник О.В.Прикладна теорія цифрових автоматів. 2001.-235с

6. В.В.Гусєв, Л.Г.Зеличенко. Основи імпульсної і цифрової техніки.М.:

Радянське радіо. 1975.

7. Під редакцією Г.Хелмса. Комп’ютери.М.:Мир.1986

8. М.А. Карцев .Арифметика цифрових машин. М.: Наука. 1969

9. С.В. Яблонський. Введення в дискретну математику. М.: Наука. 1986

10. Д. Кнут. Мистецтво програмування для ЕОМ т.2. М.: Мир. 1977

*