
- •Лекция №1. Матрицы. Основные понятия. Понятие матрицы.
- •Алгебра матриц.
- •Свойства произведения матриц.
- •Определители.
- •Определители более высокого порядка.
- •Свойства определителей
- •При транспонировании матрицы ее определитель не изменяется: .
- •Свойство антисимметрии при перестановке двух строк (столбцов).
- •3. Линейное свойство определителя.
- •Определитель суммы и произведения матриц.
- •Алгоритм вычисления обратной матрицы. (Метод присоединенной матрицы).
- •Элементарные преобразования над матрицами.
- •Ранг матрицы. Рассмотрим произвольную, необязательно квадратную, матрицу а размера mxn. Линейная зависимость строк.
- •Вычисление ранга матрицы.
- •Системы линейных алгебраических уравнений (слау).
- •Система m уравнений с n неизвестными.
- •Система n линейных уравнений с n неизвестными.
- •Система m уравнений с n неизвестными.
- •Однородные системы линейных уравнений.
Лекция №1. Матрицы. Основные понятия. Понятие матрицы.
Матрицей размера mxn называется таблица, состоящая из mxn выражений,
где m – число строк, n-число столбцов.
Обозначение:
А= или
или

Числа аij–элементы матрицы. Индекс i обозначает номер строки, а индекс j-столбца.
Если m=n, то матрица квадратная.
Если
m=1, получаем матрицу-строку А=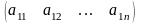 .
.
Если
n=1, получаем матрицу-столбец
 А=.
А=.
Нулевой матрицей(нуль-матрицей) называется матрица любого размера, все элементы которой нули- Обозначение 0mxn или Θ.
Если m=n – квадратная матрица. (Пример) Mn(R) – множество квадратных матриц над R.
Главной диагональю квадратной матрицы называется диагональ, идущая из левого верхнего угла матрицы в ее правый нижний угол: а11, а22, …, аnn.( Элементы вида аii- диагональные элементы)
Побочной диагональю квадратной матрицы называется диагональ, идущая из левого нижнего угла матрицы в ее правый верхний угол: аn1, аn-12, …, а1n.
Матрица
называется диагональной,
если все недиагональные элементы матрицы
равны нулю, т.е.
 ,
,
 .
Пример.
.
Пример.

След
матрицы trA=
Единичной матрицей n-го порядка называется диагональная матрица n-го порядка, все диагональные элементы которой равны 1. Обозначают буквой Е. Пример.
Выделяют так же верхние Δ-е и нижние Δ-е матрицы. Пример.
Алгебра матриц.
Две матрицы считаются равными, если эти матрицы имеют одинаковые порядки и все их соответствующие элементы совпадают. (Аnxm=Bkxl, n=k, m=l, aij=bij)
Сложение матриц. Суммой двух матриц А и В одинакового размера nxm называется матрица С=А+В того же размера nxm, элементы которой равны cij=aij+bij (i=1,…,m; j=1,…,n) (1)
Из определения следует, что операция сложения матриц обладает теми же свойствами, что и операция сложения вещественных чисел, а именно
1) А+В=В+А – св-во коммутативности.
2) (А+В)+С=А+(В+С) - св-во ассоциативности.
3) А+0=А
Умножение матрицы на число. Произведением матрицы А на вещественное число λ называется матрица В=λА, элементы которой
bij=λaij, i=1,…,m; j=1,…,n (2)
Пример.
Умножение матрицы на число обладает следующими свойствами:
1) (λμ)А=λ(μА) – сочетательное относительно числового множителя;
2) λ(А+В)=λА+λВ – распределительное относительно суммы матриц;
3) (λ+μ)А=λА+μА - распределительное относительно суммы матриц.
Разностью матриц А и В одинаковых порядков m и n называется матрица С таких же порядков, которая в сумме с матрицей В дает матрицу А. С=А-В. Матрица С может быть получена по правилу С=А+(-1)В.
Умножение матриц. Умножение матрицы А на матрицу В определено, когда число столбцов матрицы А равно числу строк матрицы в. Произведением матриц Аmxk и Bkxn называется матрица Cmxn, каждый элемент сij равен сумме произведений элементов i-й строки матрицы А на j-й столбец матрицы В: сij=ai1b1j+ ai2b2j+…+ aikbkj=
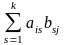 ,
i=1,2,…,m; j=1,2,…,n (3)
,
i=1,2,…,m; j=1,2,…,n (3)
Пример.
А=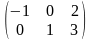 ,
В=
,
В=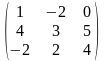 ,
АВ=
,
АВ=
Свойства произведения матриц.
1) (АВ)С=А(ВС) – ассоциативное свойство;
Доказательство.
заметим, что если Аmxn,
Bnxp,
Cpxs,
то элемент dij
матрицы
(АВ)С в силу (3) равен dij= ,
а элемент
,
а элемент
 матрицы А(ВС) равен
=
матрицы А(ВС) равен
=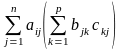 .
Тогда равенство dij=
получаем из возможности изменения
порядка суммирования относительно j и
k.
.
Тогда равенство dij=
получаем из возможности изменения
порядка суммирования относительно j и
k.
2) (А+В)С=АС+ВС или А(В+С)=АВ+АС – дистрибутивное относительно суммы матриц свойство.
Доказательство. Если матрицы А и В имеют размер m´n, а матрица С - n´k, то
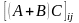 =
=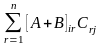 =
= =
= =
=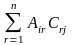 +
+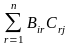 =(АС)ij+(BC)ij=(AC+BC)ij
=(АС)ij+(BC)ij=(AC+BC)ij
3) λ(АВ)=(λА)В=А(λВ) - сочетательное относительно числового множителя/
4) Существует такая матрица ЕÎ Mn(R), что "АÎ Mn(R)ÞАЕ=ЕА=А.
В качестве матрицы Е можно взять единичную матрицу.
5) "АÎ Mn(R)ÞАQ=Q (нулевая матрица).
Относительно свойства коммутативности произведения матриц отметим следующее:
1) Если произведение матриц АВ существует, то произведение ВА может и не существовать. Например, если А3х5, В5х4, то произведение АВ существует, а произведение ВА не существует, т.к. число столбцов матрицы В не равно числу строк матрицы А.
2)
Если существуют произведения АВ и ВА,
то они могут быть матрицами разных
размеров. Например, найдем АВ и ВА, если
А=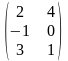 ,
В=
,
В=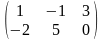

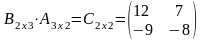 ,т.е.
,т.е.

3) Если А и В квадратные матрицы одного порядка, то произведения АВ и ВА существуют и оба являются матрицами одинакового порядка. Но при этом коммутативный (переместительный) закон умножения не выполняется, т.е. .
Например,
АВ=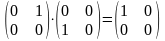 ,
ВА=
,
ВА=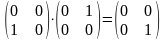
4)
Если D–диагональная матрица порядка n
такая, что все ее диагональные элементы
равны между собой D= ,
тогда
,
тогда
 справедливо равенство AD=DA. (+док-во)
справедливо равенство AD=DA. (+док-во)
Д-во.
Пусть
сij
и
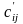 элементы, стоящие на пересечении i-й
строки и j-го столбца матриц AD и DA
соответственно. Тогда, сij=аijd,
=dаij,
т.е. сij=
.
элементы, стоящие на пересечении i-й
строки и j-го столбца матриц AD и DA
соответственно. Тогда, сij=аijd,
=dаij,
т.е. сij=
.
Кроме того, для квадратных матриц верны следующее свойство: АЕ=ЕА=А, А0=0А=0.
5.) Произведение двух ненулевых матриц может равняться нулевой матрице, те. Из того, что АВ=0 не следует, что А=0 или В=0.
Например,
А= В=
В=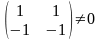 ,
АВ=
,
АВ=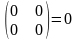
Матрицы А и В называются перестановочными, если АВ=ВА.
4)
Возведение в степень. Целой положительной
степенью Аm
(m>1)
квадратной матрицы А называется
произведение m матриц, равных А, т.е.
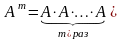 .
.
Эта операция определена только для квадратных матриц. Пример.
 ,
,
Свойства степени матрицы.
По определению: А0=Е, А1=А;
 ;
3)
;
3)
 .
.
Из того, что Аm=0 не следует, что А=0.
5)
Транспонирование матрицы – переход
от матрицы Аmxn
к матрице
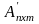 (АТ),
в которой строки и столбцы поменялись
местами с сохранением порядка. Матрица
АТ
называется транспонированной
относительно матрицы А.
(АТ),
в которой строки и столбцы поменялись
местами с сохранением порядка. Матрица
АТ
называется транспонированной
относительно матрицы А.

Пример.
А3х2=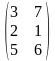 ,
,
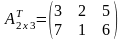
Свойства операции транспонирования. (Док-ть сам-но)
(АТ)Т=А; 3) (А+В)Т=АТ+ВТ;
(λА)Т=λАТ; 4) (АВ)Т=ВТАТ.
Доказательство. 1)((АТ)Т)ij=(AT)ji=Aij
3) (А+В)ijТ=(A+B)ji=Aji+Bji=АТ+ВТ
4)
(АВ)ijТ=(AB)ji=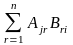 =
=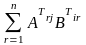 =
= =(ВТАТ)ij
=(ВТАТ)ij
Матрица
А называется симметрической,
если А=АТ.
Пример: А= /
/
Если АТ=-А, то матрица А называется кососимметрической.
Элементы симметрической матрицы, расположенные на местах, симметричных относительно главной диагонали, равны между собой.
Элементы кососимметрической матрицы, расположенные на местах, симметричных относительно главной диагонали, отличаются знаком, а диагональные равны нулю.
Блочные матрицы. Предположим, что некоторая матрица при помощи горизонтальных и вертикальных прямых разбита на отдельные прямоугольные клетки, каждая из которых представляет собой матрицу меньших размеров и называется блоком исходной матрицы. Например, матрицу
А= можно рассматривать как блочную А=
можно рассматривать как блочную А=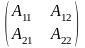 ,
где А11=
,
где А11= ,
А12=
,
А12=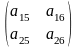 ,
А21=
,
А21= ,
А22=
,
А22=
Основные операции с блочными матрицами совершаются по тем же правилам, по которым они совершаются с числовыми матрицами, только в роли элементов выступают блоки.
Пусть блочные матрицы А=(Аab) и В=(Вbg) удовлетворяют следующим условиям: 1) Число «блочных» столбцов матрицы А совпадает с числом «блочных» строк матрицы В.
2) Для любых индексов a, b, g число столбцов у матрицы Аab совпадает с числом строк у матрицы Вbg.
Тогда
АВ=(Сag),
Сag= .
.
Пример.
 ,
,
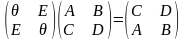 ,
,
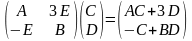 .
.
Прямой
суммой
двух квадратных матриц А и В порядков
m
и n
называется квадратная блочная матрица
С порядка m+n,
равная С=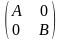 =АÅВ.
=АÅВ.
Из определения следует, что прямая сумма не является коммутативной, т.е. АÅВ¹ВÅА. Но справедливо свойство ассоциативности: (АÅВ)ÅС=АÅ(ВÅС).
В результате выполнения операций в левой и правой частях равенства получается одна и та же блочно-диагональная матрица:
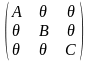
А также справедливо следующие свойства:
(АmÅAn)+(BmÅBn)=(Am+Bm)Å(An+Bn),
(AmÅAn)(BmÅBn)=AmBmÅAnBn
В этих формулах Аm и Bm – произвольные квадратные матрицы порядка m, а Аn и Bn – произвольные квадратные матрицы порядка n.
Эти записи означают следующее:
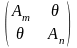 +
+ =
=
=
