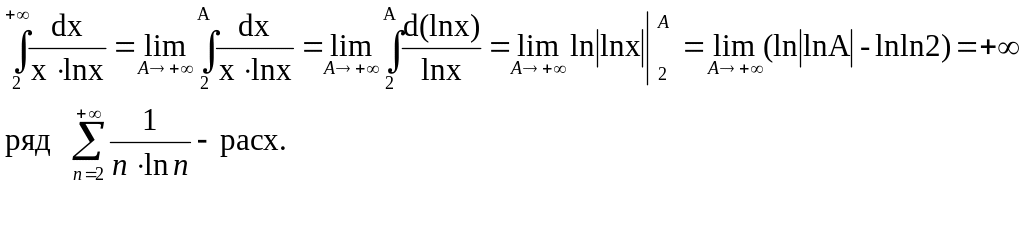16. Числові ряди. Геометричний ряд. Гармонічний ряд. Достатні ознаки збіжності рядів з додатними членами: Даламбера, Коші, інтегральна.

Пусть задана последовательность {a_n}. Символ (1), назыв. числовым рядом. При этом числа , а выражение - назыв. общим членом ряда.

Ряду (1) поставим в соответстветствие последовательность {S_n}.

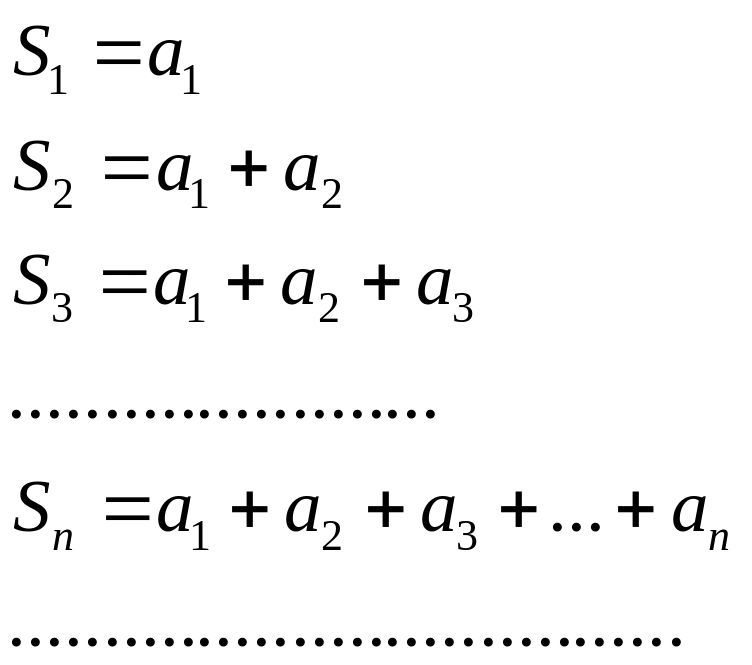(2)

Последовательность (2) назыв. последовательностью частичных сум ряда (1).

Опр. Конечный или бесконечный предел последовательности {S_n} назыв. сумой ряда, при этом записывают .

Опр. Если ряд имеет конечную суму, то он назыв. сход. в противном случае ( не существует.) ряд назыв. рассходящимся.

Замеч. Исследование сходимости рядов является другой формой исследования сходимости последовательностей так, как каждому ряду однозначно, ставится в соответствие последовательность его частичных сум, и наоборот для каждой последовательности {S_n} можно построить ряд, частичн. сумы которого будут эллементы S_n.

Опр. Ряд назыв. геометрическим если его члены образуют геометрическую прогресию

Т. Геометрический ряд сходится, если и расходьится если .

Опр.Гармоническим рядом назыв. ряд вида : .

Число b назыв. сред. гармоническим чисел a и c, если справ. равенство .

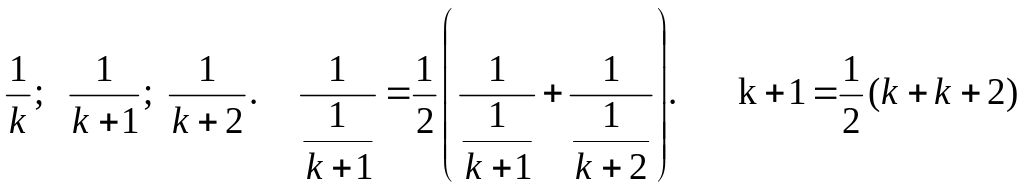
У гармонического ряда каждый член начиная со второго явл. средним гармонич. со следующим членом.

Т. Гармонический ряд расходится.

Свойства сходящихся рядов.

Опр. Ряд назыв. m-тым остатком ряда

Т1.Ряд и любой его остаток сходятся или расходятся одновременно.

Т2. Если ряд сходится, то придел его m-того остатка, при равен 0. -сх.

Т3. Если ряд с общим членом -сход. и , то -сх., причем .

Т4. Если сходятся ряды , и их сумы соответствено равны А и В, то сходятся также ряды и их сумы соответственно равны .

Т5. (необходимое условие сход. ряда) Если ряд - сх., то придел его общего члена=0.( - сх., )

Опр. Ряд назыв. положительным если все его члены неотрицательны.

Т1. (Критерий сход. полож. ряда)Для того чтобы положительний ряд был сходящимся необходимо и достаточно чтобы последовательность его частичых сум была ограничена .

Пять признаков сходимости положительних рядов

Т2. (I-признак сравнения) Пусть даны два положительных ряда , и для выполнено неравенство тогда: 1) 2) .

П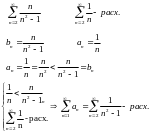 ример: 1) 2)

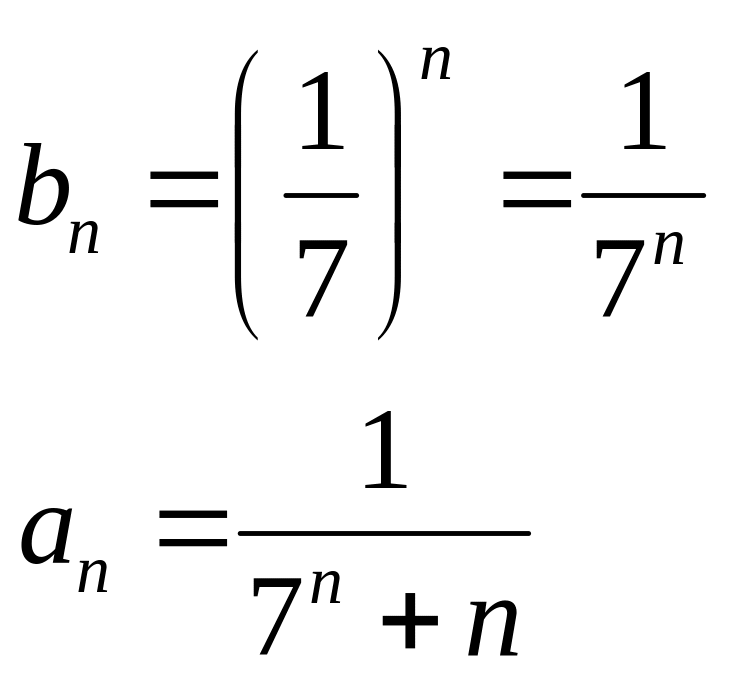
Замеч. Так как умножение числового ряда на число не изменяет его сходимости, то неравенство в теореме может быть заменено таким неравенством:

Т3. (II-признак сравнения) Пусть даны два положительных ряда ,причем члены второго ряда строго больше нуля ( ) , предположим что существует конечний или бесконечный предел , тогда: 1) данные ряди сходятся или расхдятся одновременно. 2) 3)

П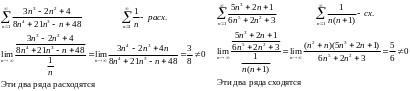 ример.:

1) 2)

Т4. (признак Даламбера)Пустя дан положительнй ряд ,и существует конечный или бесконечный предел , тогда, если:1) ряд сходится; 2) ряд расходится.

Д -во: 1)

Возьмем , так чтобы . Для выбраного

, , .

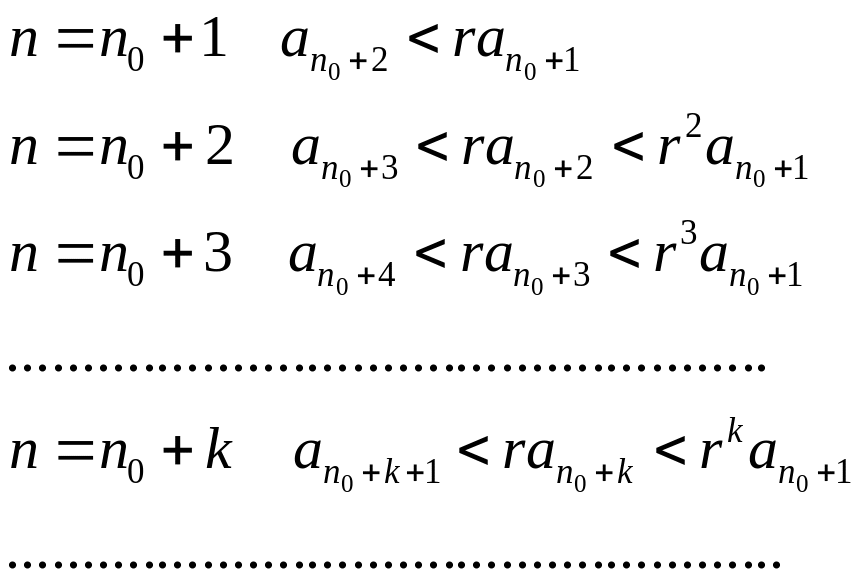
Рассмотрим ряд - геометрич ряд , , значит ряд сходящийся.

- сходится по первому признаку сравнения, так как

- сх., и является -остатком ряда значит ряд - сх.

2 )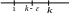

Возьмем , так чтобы . Для выбраного

, , , .

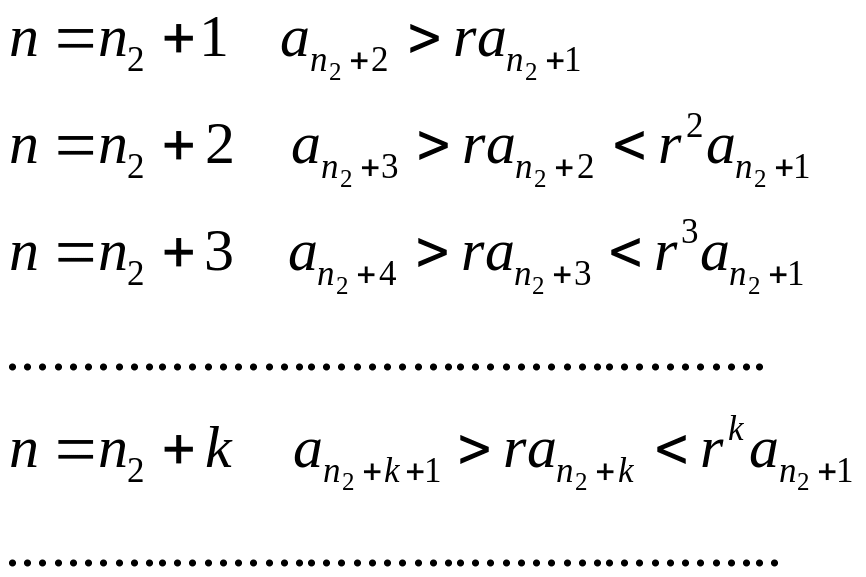Рассмотрим ряд - геометрич ряд , значит ряд расх.

- расх. по первому признаку сравнения, так как

- расх., и явл. -остатком ряда значит ряд - расх.

Замеч. 1) Легко заметить что в случае нарушено необходимое условие сходимости ряда( )

2) В случае признак Даламбера не дает ответ на вопрос о сходимости ряда, тоесть сходящиеся и расходящиеся ряды при .

Пример:

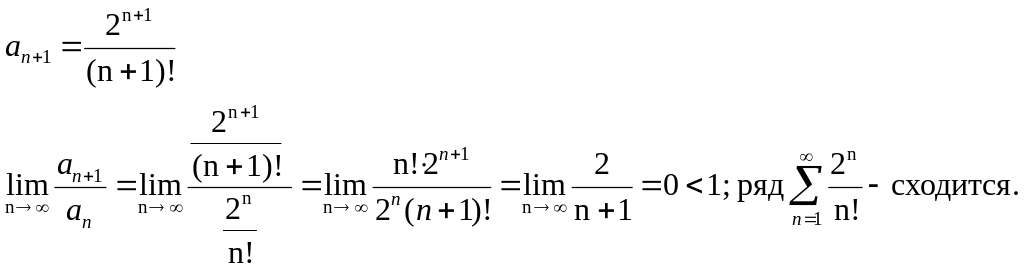
Т5. (признак Коши)Пустя для положительного ряда существует предел , тогда, если: 1) ряд сходится; 2) ряд расходится

Пример:

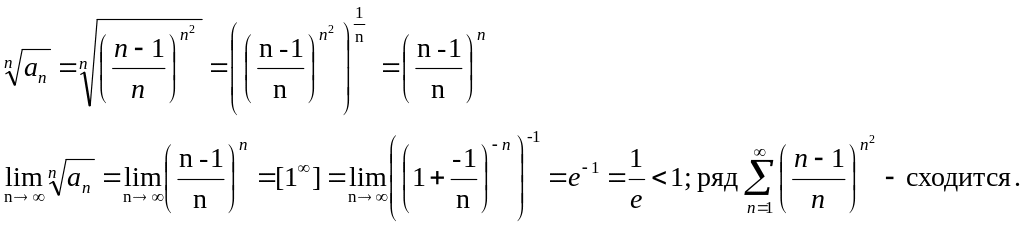
Т.(интегральный признак) Пусть функция опред. на , положительна и убывает на этом отрезке тогда, тогда ряд и несобственный интеграл сходятся или расходятся одновременно.

Замечание:Если функция определена, положительна и убывает на тогда ряд и несобственный интеграл сходятся или расходятся одновременно.

Пример. Исследов сход. ряда