
- •II. Сприймання і усвідомлення знань про похідну сталої функції, степеневої функції з цілим показником
- •VI. Підведення підсумків уроку
- •V. Домашнє завдання
- •1) Знайдіть похідні функцій
- •2) Знайдіть похідні функцій:
- •1. Знайдіть похідні функцій:
- •2. Знайдіть похідні функцій:
- •3. Знайдіть похідні функцій:
- •IV. Сприймання і усвідомлення теореми про похідну частки функцій
- •1. Знайдіть похідні функцій:
- •2. Знайдіть похідні функцій:
- •V. Домашнє завдання
- •1. Знайдіть похідні функцій:
- •2. Знайдіть похідні функцій:
- •IV. Домашнє завдання
- •IV. Сприймання і усвідомлення матеріалу про похідну степеневої функції , де
1. Знайдіть похідні функцій:
а)
у
= х3
+ х – х4; б)
 ;
;
в)
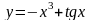 ; г)
; г)
 .
.
Відповідь:
а) ; б)
; б)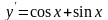 ; в)
; в)
 ;
;
г)
 .
.
2. Знайдіть значення похідної функції f(x) в точці х0:
а)
 ;
;
б)
 ;
;
в)
 .
.
Відповідь: а) 1; б) ; в)-1.
3. При яких значеннях х значення похідної функції f(x) дорівнює 0:
а) ; б)
; б)
 ; в)
; в)
 .
.
Відповідь:
а)
 ; б)
; б)
 ; в)
; в)
 .
.
ІІІ. Сприймання і усвідомлення теореми про похідну добутку
Теорема.
Якщо функції f(x)
і g(x)
диференційовані в точці х, то їхній
добуток також – диференційована функція
в цій точці і
 ,
або
коротко говорять: похідна добутку двох
функцій дорівнює сумі добутків кожної
функції на похідну другої функції
,
або
коротко говорять: похідна добутку двох
функцій дорівнює сумі добутків кожної
функції на похідну другої функції
Доведення.
Розглянемо функцію
 .
Зафіксуємо х0
і надамо аргументу приросту
,
тоді
.
Зафіксуємо х0
і надамо аргументу приросту
,
тоді
1) 
Оскільки
 ,
,
 ,
то
,
то

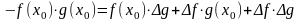 .
.
2)


 .
.
Отже,
 .
.
Наслідки
а) Постійний
множник можна винести за знак похідної:
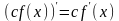 .
.
Дійсно, .
.
б) Похідна добутку декількох множників дорівнює сумі добутків похідної кожного із них на всі останні, наприклад:
 .
.
Приклад. Знайдіть похідні функцій:
а)  ;
;
б)  ;
;
в)  .
.
Розв’язування
а)  ;
;
б)

 ;
;
в)


 .
.
Виконання вправ.
1. Знайдіть похідну функцій:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Відповідь: а) 6х-5; б)  ;
;
в) 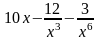 ; г)
; г)  .
.
2. Знайдіть похідні функцій:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
Відповідь: а)  ; б)
; б)  ;
;
в) 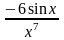 ; г)
; г)  .
.
3. Знайдіть похідні функцій:
а)  ; б)
; б)  .
.
Відповідь: а)  ;
б)
;
б)  .
.
IV. Сприймання і усвідомлення теореми про похідну частки функцій
Теорема.
Якщо функції f(x)
і g(x)
диференційовані в точці х і g(x) ,
то функція
,
то функція
 диференційована в цій точці і
диференційована в цій точці і
 .
.
Доведення
Формулу похідної частки можна вивести, скориставшись означенням похідної. Проте це зробити можна простіше.
Нехай
 ,
тоді f(x)=у(х)
,
тоді f(x)=у(х) .
Знайдемо похідну функції f(x),
скориставшись теоремою про похідну
добутку,
.
Знайдемо похідну функції f(x),
скориставшись теоремою про похідну
добутку,
 .
Виразимо з цієї формули
.
Виразимо з цієї формули


і
підставимо замість у(х) значення
 ,
тоді будемо мати:
,
тоді будемо мати:
 .
.
Отже,

 .
.
Приклад: Знайдіть похідні функцій
а)  ; б)
; б) 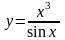 .
.
Розв’язання
а)  .
.
б)  .
.
Виконання вправ
1. Знайдіть похідні функцій:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
Відповідь: а)  ; б)
;
; б)
;
в)  ; г)
; г)  .
.
2. Знайдіть похідні функцій:
а) 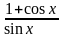 ; б)
; б)  ; в)
; в)  ; г)
; г) 
Відповідь: а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
V. Домашнє завдання
Розділ VII § 4. Запитання і завдання для повторення розділу VII № 23 – 27. вправа № 10 (1 -5, 7 - 8).
ТЕМА УРОКУ: Похідна складеної функції
Мета уроку: Формування поняття про похідну складеної функції, знань учнів про похідну складеної функції, умінь знаходити похідну складеної функції.
І. Перевірка домашнього завдання
1)  ;
;
2)

 ;
;
3) 
 ;
;
4)  ;
;
5)  ;
;
6)  .
.
2. Самостійна робота.
Варіант 1.
1. Знайдіть значення похідної функції f(x) при заданому значенні аргументу х0:
а)  ,
х0=-1. (2
бали)
,
х0=-1. (2
бали)
б) 
 . (2
бали)
. (2
бали)
2. Знайдіть похідну функцій:
а)  . (2
бали)
. (2
бали)
б)  . (2
бали)
. (2
бали)
в) 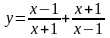 . 42
бали)
. 42
бали)
Варіант 2.
1. Знайдіть значення похідної функції f(x) при заданому значенні аргумента х0:
а)  ,
х0=-1. (2
бали)
,
х0=-1. (2
бали)
б) 
 . (2
бали)
. (2
бали)
2. Знайдіть похідну функцій:
а)  . (2
бали)
. (2
бали)
б)  . (2
бали)
. (2
бали)
в)  . 42
бали)
. 42
бали)
Відповідь:
В-1.
1. а)
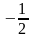 ; б)
-1
; б)
-1
2.
а)
 ; б)
; б)
 ; в)
; в)

В-2.
1. а)
 ; б)
1
; б)
1
2.
а)
 ; б)
; б)
 ; в)
; в)
 .
.
ІІ. Сприймання і усвідомлення поняття складеної функції та її похідної
Розглянемо приклад.
Приклад
1. Нехай
треба обчислити по заданому значенню
х значення функції у, яка задана формулою
 .
.
Для
цього спочатку треба обчислити за даним
значенням х значення u=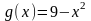 ,
а потім за значенням u обчислити у=
,
а потім за значенням u обчислити у= .
.
Отже,
функція g
ставить у відповідність числу х число
u, а функція f
– числу u число у. Говорять, що у є
складеною функцією із функції g
і f,
і пишуть
 .
.
Функцію g(х) називають внутрішньою функцією, або проміжною змінною, функцію f(u) – зовнішньою функцією. Отже, щоб обчислити значення складеної функції в довільній точці х, спочатку обчислюють значення u внутрішньої функції g, а потім f(u).
Приклад
2. Розглянемо
функцію
 .
Вона
є складною із функцій
.
Вона
є складною із функцій

 ,
де
,
де
 - внутрішня функція,
- внутрішня функція,
 - зовнішня функція.
- зовнішня функція.
Приклад
3. Запишіть
складні функції
 і
і
 ,
якщо
,
якщо
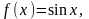

Розв’язання
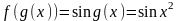

Виконання вправ.
1.
Задайте формулою елементарні функції
 і
і
 ,
із яких побудована складна функція
:
,
із яких побудована складна функція
:
а) б)
б)

в) г)
г)

Відповіді: а)


б)
 ;
;
в)


г)
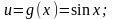
 .
.
2.
Дано функції:
 .
Побудуйте функції:
.
Побудуйте функції:
а)
; в)
 ; в)
; в)
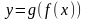 ;
;
г)
 ; в)
; в)
 ; є)
; є)
 .
.
Відповідь:
а)
 ; б)
; б)
 ;
;
в)
 ; г)
; г)
 ;
;
д)
 є)
є)

У
складній функції
присутня проміжна змінна
 .
Тому при знаходженні похідної складної
функції ми будемо вказувати, по якій
змінній взято похідну, використовуючи
при цьому спеціальні показники:
.
Тому при знаходженні похідної складної
функції ми будемо вказувати, по якій
змінній взято похідну, використовуючи
при цьому спеціальні показники:
 – похідна
функції у по аргументі х;
– похідна
функції у по аргументі х;
 – похідна
функції у по аргументі u;
– похідна
функції у по аргументі u;
 – похідна
функції u
по аргументі х;
– похідна
функції u
по аргументі х;
Теорема. Похідна
складеної функції
знаходиться
за формулою
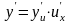 ,
де
,
або похідна складеної функції дорівнює
похідній зовнішньої функції по проміжній
змінній, помноженій на похідну внутрішньої
функції по основному аргументу.
,
де
,
або похідна складеної функції дорівнює
похідній зовнішньої функції по проміжній
змінній, помноженій на похідну внутрішньої
функції по основному аргументу.
Доведення
Будемо
вважати, що функція
має похідну в точці х0,
а функція
 має похідну в точці u0=
має похідну в точці u0= ,
тобто існують границі
,
тобто існують границі
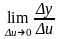 ,
,
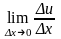 і
і
 .
.
Нехай,
аргументу х0
надано приросту
,
тоді змінна u набуде приросту
 .
Поскільки
.
Поскільки
 одержала приріст
одержала приріст
 ,
то функція у одержить також приріст
,
то функція у одержить також приріст
 .
Приріст
зумовив
виникнення приросту
і
.
Приріст
зумовив
виникнення приросту
і
 .
.
Подамо
 .
Перейдемо до границі при
.
Перейдемо до границі при
 (при цьому
(при цьому
![]() ).
).
 або
або
 .
.
Приклад 1. Знайдіть похідну функції у = (3х3-1)5.
Розв’язання
у
= (3х3-1)5
– складена функція
 ,
де u =3х3-1,
тоді
,
,
де u =3х3-1,
тоді
,

 .
.
При обчисленні похідної складеної функції явне введення допоміжної букви u для позначення проміжного аргументу не є обов’язковим. Тому похідну даної функції знаходять відразу як добуток похідної степеневої функції u5 на похідну від функції 3х3-1:
 .
.
Приклад 2.Знайдіть похідні функцій:
а)
; б)  ;
;
в)  ; г)
; г)  .
.
Розв’язання
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
Виконання вправ.
