3.4.1Искажения сигналов, вызванные ограниченностью ачх

Влияние на форму сигнала ограниченности АЧХ рассмотрим на примере идеального низкочастотного фильтра. Пусть АЧХ ограничена частотой , а ФЧХ линейна. На вход подан единичный скачок u(t).

Определим реакцию на этот входной сигнал. Спектр u(t) нами получен ранее:

.

Спектр выходного сигнала для идеального низкочастотного фильтра будет:

Выходной сигнал, как функция времени, определяется обратным преобразованием Фурье.

Интеграл в элементарных функциях не выражается. Но он табулирован и называется интегральным синусом. График его приведен на рисунке (а).

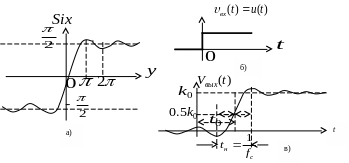
Р

Реакция фильтра на единичный скачек (б) представлена на рисунке (в). Как видно из рисунка выходной сигнал запаздывает на время имеет колебательный характер на вершине, амплитуда его превышает на 9%; фронт имеет конечную крутизну, причем время нарастания, определенное как промежуток от наименьшего до наибольшего значения амплитуды сигнала, обратно пропорционально частоте среза. В литературе известны и другие определения времени нарастания, например, по пересечениям касательной с осью абсцисс и уровнем (тогда ) или от 0,1 до 0,9 установившиеся значения.

На рисунке мы видим и парадокс, нарушение принципа причинности. Система реагирует на входной сигнал еще до подачи его на вход (колебательность у основания скачка). Причина этого явления в том, что идеальный фильтр относится к числу физически нереализуемых, т.к. его АЧХ и ФЧХ выбраны произвольно и независимо друг от друга. Для реализуемых фильтров АЧХ и ФЧХ связаны друг с другом преобразованием Гильберта. К этому вопросу мы вернемся позже.

Из полученного результата легко найти реакцию фильтра на прямоугольный импульс длительностью . Его можно представить как разность двух скачков . Тогда будет суперпозицией двух интегральных синусов.

t

Очевидно, что при передаче данных по каналу с полосой длительность символа не может быть меньше чем . Следовательно, существует верхний предел (граница) скорости модуляции, называемый пределом Найквиста.

. Для телефонного канала, например,

3.4.2Искажения сигнала из-за нелинейности фчх

Влияние фазочастотных искажений рассмотрим для сигнала произвольной формы, но с ограниченным спектром [ ]. Коэффициент передачи фильтра будем считать равным , где - нелинейная функция. Пусть, например,

.

Такой функцией достаточно хорошо аппроксимируется ФЧХ четырехпроводного телефонного канала без фазовой коррекции.

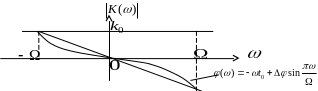
Выходной сигнал находится как обратное преобразование Фурье от спектра выходного сигнала:

Воспользуемся представлением в виде ряда по бесселевым функциям для .

Тогда,

Если невелико, то , а и

.

Поскольку ранее мы ввели величину время нарастания , можно считать, что . Тогда .

Выходной сигнал получается суперпозицией трех сигналов: основного, опережающего эхо-сигнала и отстающего эхо-сигнала, изображенных на рисунке.

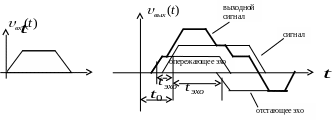
Форма эхо-сигналов совпадает с формой основного, а амплитуда определяется величиной - половиной максимального отклонения от линейности.

Итак, при фазовых искажениях колебательного вида переходный процесс перестает быть нечетно-симметричным относительно своей средней точки, удлиняется время переходного процесса. «Эхо-сигналы» являются помехой для соседних импульсов, т.е. имеет место межсимвольная интерференция.