4.4Потенциальная помехоустойчивость

Помехоустойчивость это способность системы правильно воспринимать сигналы, несмотря на искажения их и наличие непредсказуемых помех. Для дискретных сигналов помехоустойчивость можно оценить или измерить через вероятность правильного приема. Предельно достижимую в заданных условиях приема помехоустойчивость называют потенциальной помехоустойчивостью. Вопросы анализа помехоустойчивости различных систем передачи информации являются предметом теории потенциальной помехоустойчивости, которая была разработана Котельниковым в 1946 году. В частности, им была решена задача при следующих ограничениях:

1. Сигнал и шум аддитивны

2. Закон распределения шума в канале нормальный

3. Шум в канале белый, т.е. отсчеты некоррелированы и

4. На приемном конце имеется полная информация о сигналах и вплоть до момента их существования

В силу аддитивности и взаимной независимости сигналов и помех для любого момента времени , лежащего на интервале условный закон распределения шума при наличии сигнала будет иметь вид:

.

Отношение правдоподобия, следовательно, будет для момента иметь вид:

.

На интервале , если сигналы ограничены по спектру, можно взять независимых отсчетов.

Тогда по совокупности отсчетов имеем:

.

Если , то устреми для белого шума получим в пределе:

.

Если в качестве критерия приема выбрать критерий максимального правдоподобия Фишера, решение принимается сравнением с 1. Но это равносильно сравнению показателя у экспоненты с нулем. Получаем, следовательно, такую структурную схему приемника, принимающего решения по наблюдаемым реализациям сигналов с помехами:

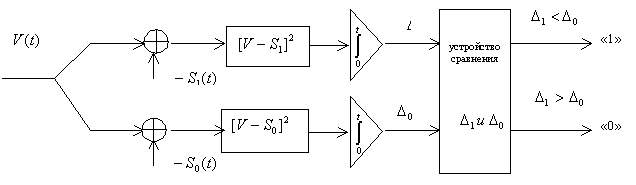
Сравниваемые интегралы можно преобразовать, тогда получим другие варианты возможных реализаций оптимальных приемников.

Сравнивать надо как следует из последнего выражения ( и - энергия сигналов единицы и нуля).

.

Здесь Е₀ – энергия сигнала «0», Е₁ – энергия сигнала «1».

Корреляционный приемник для этого варианта следующий:

Если энергии сигналов равны, схема упрощается и приобретается весьма ценное свойство – нечувствительность к уровню входного сигнала.

4.5Приемник на согласованных фильтрах

Реакция фильтра на входное воздействие может быть найдена как интеграл свертки .

Подберем такой фильтр, чтобы к моменту его выходная реакция была равна величине интеграла . Если сигнал поступит на вход в момент , то должно быть .

Отсюда , обозначим , получим . Фильтр, импульсная переходная функция которого удовлетворяет последнему условию, называют согласованным с сигналом. График для является зеркальным отображением сигнала , когда зеркало помещено в точку и отсчет начинается от плоскости зеркала.

Найдем комплексный коэффициент согласованного фильтра.

С точностью до амплитудного множителя и постоянной задержки передаточная функция согласованного фильтра является комплексно-сопряженной со спектром сигнала.

.

Найдем выходной сигнал согласованного фильтра:

В соответствии с теоремой Релея при выходной сигнал равен:

,

т .е. все спектральные составляющие выходного сигнала совпадают по фазе и в сумме дают максимальное значение , равное энергии сигнала. Во все остальные моменты времени фазы спектральных составляющих различны и пика амплитуды сигнала не будет. Функциональная схема приемника на согласованных фильтрах будет следующей:

Выясним, с какой целью в последней схеме введен детектор огибающей. Для этого получим формулу для выходного сигнала как функцию времени. Пусть, например, входной сигнал , , шум отсутствует.

Для корреляционного приемника:

Для оптимального согласованного фильтра , будем полагать выбранным так, что , т.е. на интервале укладывается целое число периодов опорной частоты. Тогда .

Графики процесса накопления будут: