
- •Основная и расширенная матрицы системы линейных уравнений
- •Приложения дифференциального исчисления фоп_ исследование функций с помощью графиков
- •Приложения дифференциального исчисления фоп_ экстремумы функции
- •Свойства определителей
- •Системы линейных уравнений. Метод Гаусса
- •Собственные значения матрицы
- •Типы уравнений прямой
- •Точечные оценки параметров распределения
- •Точечные оценки параметров распределения_ оценка дисперсии
- •Точечные оценки параметров распределения_ оценка математического ожидания
- •Транспортная задача
- •Формула полной вероятности
Собственные значения матрицы
1. Собственные
значения собственных векторов линейного
преобразования, заданного в некотором
базисе матрицей
 ,
могут быть найдены по формуле…
a)
,
могут быть найдены по формуле…
a)
 b)
b)
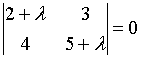 c)
c)
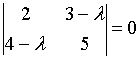 d)
d)

2. Собственные
значения собственных векторов линейного
преобразования, заданного в некотором
базисе матрицей
 ,
могут быть найдены по формуле…
a)
,
могут быть найдены по формуле…
a)
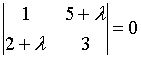 b)
b)
 c)
c)
 d)
d)

3. Собственные
значения собственных векторов линейного
преобразования, заданного в некотором
базисе матрицей
 ,
могут быть найдены по формуле…
a)
,
могут быть найдены по формуле…
a)
 b)
b)
 c)
c)
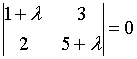 d)
d)
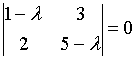
4. Собственные
значения собственных векторов линейного
преобразования, заданного в некотором
базисе матрицей
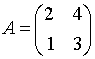 ,
могут быть найдены по формуле…
a)
,
могут быть найдены по формуле…
a)
 b)
b)
 c)
c)
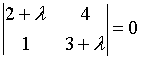 d)
d)
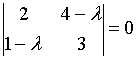
5. Собственные
значения собственных векторов линейного
преобразования, заданного в некотором
базисе матрицей
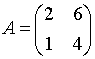 ,
могут быть найдены по формуле…
a)
,
могут быть найдены по формуле…
a)
 b)
b)
 c)
c)
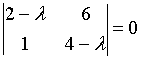 d)
d)

6. Собственные
значения собственных векторов линейного
преобразования, заданного в некотором
базисе матрицей
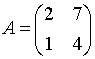 ,
могут быть найдены по формуле…
a)
,
могут быть найдены по формуле…
a)
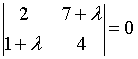 b)
b)
 c)
c)
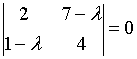 d)
d)
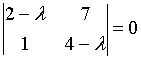
7. Собственные
значения собственных векторов линейного
преобразования, заданного в некотором
базисе матрицей
 ,
могут быть найдены по формуле…
a)
,
могут быть найдены по формуле…
a)
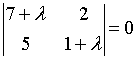 b)
b)
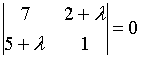 c)
c)
 d)
d)

8. Собственные
значения собственных векторов линейного
преобразования, заданного в некотором
базисе матрицей
 ,
могут быть найдены по формуле…
a)
,
могут быть найдены по формуле…
a)
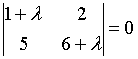 b)
b)
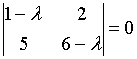 c)
c)
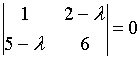 d)
d)
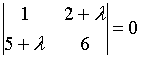
9. Собственные
значения собственных векторов линейного
преобразования, заданного в некотором
базисе матрицей
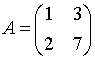 ,
могут быть найдены по формуле…
a)
,
могут быть найдены по формуле…
a)
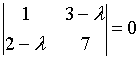 b)
b)
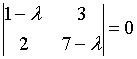 c)
c)
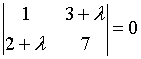 d)
d)

10. Собственные
значения собственных векторов линейного
преобразования, заданного в некотором
базисе матрицей
 ,
могут быть найдены по формуле…
a)
,
могут быть найдены по формуле…
a)
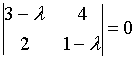 b)
b)
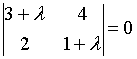 c)
c)
 d)
d)

Статистическое распределение выборки
1. Из генеральной
совокупности извлечена выборка объема
n=60,
полигон частот которой имеет вид
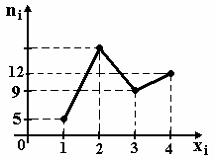 Тогда
число вариант xi=2
в выборке равно…
a) 33
b)
35
c) 34
d)
60
Тогда
число вариант xi=2
в выборке равно…
a) 33
b)
35
c) 34
d)
60
2. Из генеральной
совокупности извлечена выборка объема
n=40,
полигон частот которой имеет вид
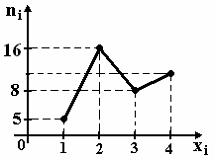 Тогда
число вариант xi=4
в выборке равно…
a) 10
b)
12
c) 11
d)
40
Тогда
число вариант xi=4
в выборке равно…
a) 10
b)
12
c) 11
d)
40
3. Из генеральной
совокупности извлечена выборка объема
n=70,
полигон частот которой имеет вид
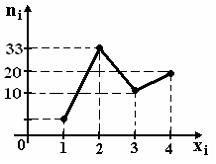 Тогда
число вариант xi=1
в выборке равно…
a) 70
b)
8
c) 7
d)
6
Тогда
число вариант xi=1
в выборке равно…
a) 70
b)
8
c) 7
d)
6
4. Из генеральной
совокупности извлечена выборка объема
n=80,
полигон частот которой имеет вид
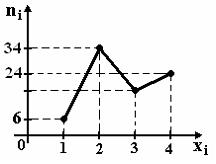 Тогда
число вариант xi=3
в выборке равно…
a) 17
b)
15
c) 80
d)
16
Тогда
число вариант xi=3
в выборке равно…
a) 17
b)
15
c) 80
d)
16
5. Из генеральной
совокупности извлечена выборка объема
![]() ,
полигон частот которой имеет вид:
,
полигон частот которой имеет вид:
 Тогда
число вариант
Тогда
число вариант
![]() в
выборке равно…
a) 10
b)
48
c) 8
d)
9
в
выборке равно…
a) 10
b)
48
c) 8
d)
9
6. Из генеральной
совокупности извлечена выборка объема
![]() ,
полигон частот которой имеет вид:
,
полигон частот которой имеет вид:
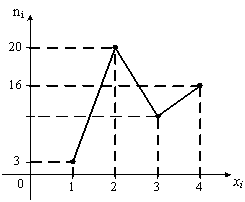 Тогда
число вариант
в
выборке равно…
a) 49
b)
10
c) 9
d)
11
Тогда
число вариант
в
выборке равно…
a) 49
b)
10
c) 9
d)
11
7. Из генеральной
совокупности извлечена выборка объема
![]() ,
полигон частот которой имеет вид:
Тогда
число вариант
в
выборке равно…
a) 12
b)
11
c) 10
d)
50
,
полигон частот которой имеет вид:
Тогда
число вариант
в
выборке равно…
a) 12
b)
11
c) 10
d)
50
8. Из генеральной
совокупности извлечена выборка объема
![]() ,
полигон частот которой имеет вид:
,
полигон частот которой имеет вид:
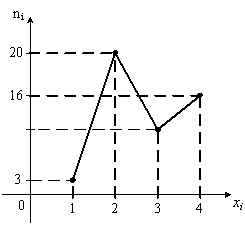 Тогда
число вариант
в
выборке равно…
a) 11
b)
12
c) 51
d)
13
Тогда
число вариант
в
выборке равно…
a) 11
b)
12
c) 51
d)
13
9. Из генеральной
совокупности извлечена выборка объема
![]() ,
полигон частот которой имеет вид:
,
полигон частот которой имеет вид:
 Тогда
число вариант
в выборке равно…
a) 13
b)
14
c) 52
d)
12
Тогда
число вариант
в выборке равно…
a) 13
b)
14
c) 52
d)
12
10. Из генеральной
совокупности извлечена выборка объема
![]() ,
полигон частот которой имеет вид:
Тогда
число вариант
в
выборке равно…
a) 13
b)
15
c) 14
d)
53
,
полигон частот которой имеет вид:
Тогда
число вариант
в
выборке равно…
a) 13
b)
15
c) 14
d)
53
Степенные ряды
1. Радиус сходимости
степенного ряда
 равен
9, тогда интервал сходимости имеет
вид…
a) (0;9)
b)
(–9;0)
c)
(–4,5;4,5)
d)
(–9;9)
равен
9, тогда интервал сходимости имеет
вид…
a) (0;9)
b)
(–9;0)
c)
(–4,5;4,5)
d)
(–9;9)
2. Радиус сходимости степенного ряда равен 8, тогда интервал сходимости имеет вид… a) (–8;8) b) (0;8) c) (–8;0) d) (–4;4)
3. Радиус сходимости степенного ряда равен 7, тогда интервал сходимости имеет вид… a) (–7;7) b) (0;7) c) (–3,5;3,5) d) (–7;0)
4. Радиус сходимости степенного ряда равен 6, тогда интервал сходимости имеет вид… a) (–6;0) b) (0;6) c) (–3;3) d) (–6;6)
5. Радиус сходимости степенного ряда равен 5, тогда интервал сходимости имеет вид… a) (0;5) b) (–5;0) c) (–5;5) d) (–2,5;2,5)
6. Радиус сходимости степенного ряда равен 4, тогда интервал сходимости имеет вид… a) (–2;2) b) (–4;0) c) (–4;4) d) (0;4)
7. Радиус сходимости степенного ряда равен 3, тогда интервал сходимости имеет вид… a) (–3;0) b) (0;3) c) (–3;3) d) (–1,5;1,5)
8. Радиус сходимости степенного ряда равен 12, тогда интервал сходимости имеет вид… a) (–12;0) b) (–12;12) c) (0;12) d) (–6;6)
9. Радиус сходимости степенного ряда равен 14, тогда интервал сходимости имеет вид… a) (–14;0) b) (0;14) c) (–7;7) d) (–14;14)
10. Радиус сходимости степенного ряда равен 16, тогда интервал сходимости имеет вид… a) (–16;16) b) (0;16) c) (–16;0) d) (–8;8)
Степенные ряды_ область сходимости
1. Радиус сходимости
степенного ряда
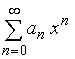 равен
9. Тогда интервал сходимости имеет
вид…
a) (–
9; 0)
b) (0; 9)
c)
(– 4,5; 4,5)
d)
(– 9; 9)
равен
9. Тогда интервал сходимости имеет
вид…
a) (–
9; 0)
b) (0; 9)
c)
(– 4,5; 4,5)
d)
(– 9; 9)
2. Радиус сходимости степенного ряда равен 8. Тогда интервал сходимости имеет вид… a) (– 8; 0) b) (– 8; 8) c) (0; 8) d) (– 4; 4)
3. Радиус сходимости степенного ряда равен 7. Тогда интервал сходимости имеет вид… a) (– 3,5; 3,5) b) (– 7; 0) c) (0; 7) d) (– 7; 7)
4. Радиус сходимости степенного ряда равен 6. Тогда интервал сходимости имеет вид… a) (– 3; 3) b) (– 6; 0) c) (– 6; 6) d) (0; 6)
5. Радиус сходимости степенного ряда равен 5. Тогда интервал сходимости имеет вид… a) (– 2,5; 2,5) b) (– 5; 0) c) (– 5; 5) d) (0; 5)
6. Радиус сходимости степенного ряда равен 4. Тогда интервал сходимости имеет вид… a) (– 4; 4) b) (0; 4) c) (– 4; 0) d) (– 2; 2)
7. Радиус сходимости степенного ряда равен 3. Тогда интервал сходимости имеет вид… a) (– 3; 0) b) (– 1,5; 1,5) c) (– 3; 3) d) (0; 3)
8. Радиус сходимости степенного ряда равен 12. Тогда интервал сходимости имеет вид… a) (– 6; 6) b) (– 12; 12) c) (0; 12) d) (– 12; 0)
9. Радиус сходимости степенного ряда равен 14. Тогда интервал сходимости имеет вид… a) (0; 14) b) (– 7; 7) c) (– 14; 0) d) (– 14; 14)
10. Радиус сходимости степенного ряда равен 16. Тогда интервал сходимости имеет вид… a) (0; 16) b) (– 8; 8) c) (– 16; 0) d) (– 16; 16)
Сходимость числовых рядов. Признак Даламбера
1. Если
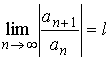 ,
то числовой ряд сходится при l,
равном ….
a) 1,9
b)
0,6
c) –
1,9
d) 1,6
,
то числовой ряд сходится при l,
равном ….
a) 1,9
b)
0,6
c) –
1,9
d) 1,6
2. Если , то числовой ряд сходится при l, равном …. a) 0,3 b) – 2,1 c) 2,1 d) 1,3
3. Если , то числовой ряд сходится при l, равном …. a) 1,8 b) 1,4 c) 0,4 d) – 1,8
4. Если , то числовой ряд сходится при l, равном …. a) 0,2 b) – 1,7 c) 1,2 d) 1,7
5. Если , то числовой ряд сходится при l, равном …. a) 0,7 b) 1,7 c) – 2,2 d) 2,2
6. Если , то числовой ряд сходится при l, равном …. a) – 3 b) 1,8 c) 3 d) 0,8
7. Если , то числовой ряд сходится при l, равном …. a) 3,5 b) 0,9 c) – 3,5 d) 1,9
8. Если , то числовой ряд сходится при l, равном …. a) 2,5 b) 1,65 c) – 2,5 d) 0,65
9. Если , то числовой ряд сходится при l, равном …. a) 1,5 b) 1,71 c) 0,71 d) – 1,5
10. Если , то числовой ряд сходится при l, равном …. a) – 1,9 b) 1,9 c) 0,52 d) 1,52
Сходимость числовых рядов_ признак Даламбера
1. Если , то числовой ряд сходится при l, равном …. a) – 1,9 b) – 0,6 c) 1,9 d) 0,6
2. Если , то числовой ряд сходится при l, равном …. a) – 1,8 b) 1,8 c) 0,7 d) – 0,7
3. Если , то числовой ряд сходится при l, равном …. a) 1,7 b) – 0,8 c) 0,8 d) – 1,7
4. Если , то числовой ряд сходится при l, равном …. a) 0,9 b) – 1,6 c) – 0,9 d) 1,6
5. Если , то числовой ряд сходится при l, равном …. a) 0,4 b) – 1,5 c) – 0,4 d) 1,5
6. Если , то числовой ряд сходится при l, равном …. a) – 1,4 b) – 0,3 c) 1,4 d) 0,3
7. Если , то числовой ряд сходится при l, равном …. a) 1,3 b) 0,2 c) – 1,3 d) – 0,2
8. Если , то числовой ряд сходится при l, равном …. a) – 1,2 b) 0,1 c) 1,2 d) – 0,1
9. Если , то числовой ряд сходится при l, равном …. a) 2,1 b) 0,51 c) – 2,1 d) – 0,51
10. Если , то числовой ряд сходится при l, равном …. a) 2,2 b) 0,65 c) – 2,2 d) – 0,65
Теоремы сложения и умножения вероятностей_ вероятность появления хотя бы одного события
1. Два стрелка производят по одному выстрелу. Вероятность попадания в цель для первого и второго стрелков равны 0,8 и 0,9 соответственно. Тогда вероятность того, что цель будет поражена, равна … a) 0,72 b) 0,98 c) 0,998 d) 0,28
2. Два стрелка производят по одному выстрелу. Вероятность попадания в цель для первого и второго стрелков равны 0,6 и 0,9 соответственно. Тогда вероятность того, что цель будет поражена, равна … a) 0,996 b) 0,46 c) 0,54 d) 0,96
3. Два стрелка производят по одному выстрелу. Вероятность попадания в цель для первого и второго стрелков равны 0,7 и 0,9 соответственно. Тогда вероятность того, что цель будет поражена, равна … a) 0,97 b) 0,37 c) 0,997 d) 0,63
4. Два стрелка производят по одному выстрелу. Вероятность попадания в цель для первого и второго стрелков равны 0,5 и 0,9 соответственно. Тогда вероятность того, что цель будет поражена, равна … a) 0,45 b) 0,95 c) 0,995 d) 0,55
5. Два стрелка производят по одному выстрелу. Вероятность попадания в цель для первого и второго стрелков равны 0,4 и 0,9 соответственно. Тогда вероятность того, что цель будет поражена, равна … a) 0,36 b) 0,94 c) 0,64 d) 0,994
6. Два стрелка производят по одному выстрелу. Вероятность попадания в цель для первого и второго стрелков равны 0,8 и 0,7 соответственно. Тогда вероятность того, что цель будет поражена, равна … a) 0,56 b) 0,94 c) 0,994 d) 0,44
7. Два стрелка производят по одному выстрелу. Вероятность попадания в цель для первого и второго стрелков равны 0,8 и 0,6 соответственно. Тогда вероятность того, что цель будет поражена, равна … a) 0,992 b) 0,52 c) 0,92 d) 0,48
8. Два стрелка производят по одному выстрелу. Вероятность попадания в цель для первого и второго стрелков равны 0,8 и 0,5 соответственно. Тогда вероятность того, что цель будет поражена, равна … a) 0,60 b) 0,40 c) 0,90 d) 0,99
9. Два стрелка производят по одному выстрелу. Вероятность попадания в цель для первого и второго стрелков равны 0,8 и 0,4 соответственно. Тогда вероятность того, что цель будет поражена, равна … a) 0,88 b) 0,32 c) 0,68 d) 0,988
10. Два стрелка производят по одному выстрелу. Вероятность попадания в цель для первого и второго стрелков равны 0,7 и 0,6 соответственно. Тогда вероятность того, что цель будет поражена, равна … a) 0,988 b) 0,88 c) 0,58 d) 0,42
