Переход к классической механике
Квантовая механика заключает в себе классическую как некоторый предельный случай. Рассмотрим, каким образом осуществляется этот предельный переход.
В
квантовой механике частица описывается
волновой функцией, которая является
решением уравнения Шредингера. В
классической механике частица
рассматривается как точка, которая
движется по траектории, полностью
определяющейся уравнениями движения.
Известно, что предельный переход от
волновой к геометрической оптике
происходит при
.
Аналогично, переход от квантовой механики
к классической можно осуществить, если
(то есть от дискретного изменения
физической величины перейти к
непрерывному).
Математически переход к геометрической оптике означает, что фаза некоторой функции, которая описывает волновой процесс, изменяется очень быстро по сравнению с амплитудой, которая изменяется медленно. Соответственно полагаем, что предельному случаю классической механики в квантовой механике отвечают волновые функции вида
,
(1.56)
где
– функция, медленно изменяющаяся, а
фаза принимает большие значения. Величину
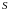называют действием.
Подставив (1.56) в уравнение Шредингера (1.42) и приравняв нулю действительные и мнимые части, получим два уравнения
(1.57)
.
(1.58)
Пренебрегая
в (1.57) членом с
,
получаем известное классическое
уравнение Гамильтона-Якоби для действия
частицы
.
(1.59)
Таким образом, при классическая механика справедлива с точностью до величин первого порядка по включительно.
Уравнение
(1.58) после умножения на
,
можно преобразовать к виду
.
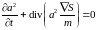(1.60)
Здесь
является плотностью вероятности
нахождения частицы в том или ином месте
пространства, а выражение
представляет классическую скорость
частицы. Следовательно, соотношение
(1.60) является уравнением непрерывности,
которое показывает, что плотность
вероятности перемещается по законам
классической механики с классической
скоростью в каждой точке.
Свободное движение микрочастицы
Рассмотрим некоторые самые простые случаи движения микрочастицы в потенциальных полях. Начнем со свободного движения.
Оператор Гамильтона в этом случае имеет вид
.
Представляя волновую функцию в виде
(1.61))
и используя метод разделения переменных, получим функцию , которая зависит от времени
,
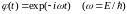(1.62)
и амплитудное уравнение Шредингера (или уравнение для стационарных состояний)
.
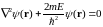(1.63)
Систему координат выбираем таким образом, чтобы направление движения частицы совпадало с осью . Тогда решение уравнения (1.63) будет иметь вид
,
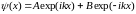(1.64)
где
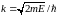(по физическому содержанием это волновой
вектор).
Значения
энергии, как видно из (1.64) оказываются
двукратно вырожденными. Это вырождение
снимается, если потребовать, чтобы кроме
энергии в этом состоянии имела определенные
значения еще какая-либо физическая
величина, например, импульс. Тогда
частице, которая движется в положительном
направлении оси
,
соответствуют импульс
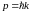и энергия
.
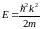Им отвечает собственная волновая функция
.
(1.65)
Ввиду
непрерывности энергетического спектра
нормировать (1.65) следует не на единицу,
а на
-
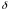функцию
.
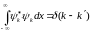(1.66)
Используя интегральное представление - функции
,
получим
для коэффициента
.
Следовательно, волновая функция свободной микрочастицы (волна де Бройля) имеет вид
.
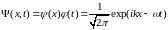(1.67)